Transformationen bezieht sich auf Operationen wie das Verschieben (auch Versetzen genannt), Drehen und Skalieren von Objekten. Sie werden in der 3D-Programmierung gespeichert, mittels Matrices, welche nichts anderes sind als rechteckige Anordnungen von Zahlen. Mehrere Transformationen können bei Verwendung von Matrices sehr schnell bewältigt werden. Im Endeffekt kann eine [4x4]-Matrix alle Transformationen repräsentieren. Über eine vereinheitlichte Matrix-Dimension für alle Transformationen zu verfügen spart Zeit bei der Berechnung.
$$\begin{array}{rcc} \mbox{Matrix}&\begin{array}{cccc} c1& c2&c3&c4\end{array}\\\begin{array}{c}Zeile(1)\\Zeile(2)\\Zeile(3)\\Zeile(4)\end{array}& \left[\begin{array}{cr} +&+&+&+\\ +&+&+&+\\ +&+&+&+\\ +&+&+&+\end{array}\right] \end{array}$$2.1 Matrixoperationen
Die relevanteste aller Operationen in Computergrafiken ist die Matrixmultiplikation. Hierauf wollen wir etwas näher eingehen.
Matrixmultiplikation
Matrixmultiplikation wird verwendet, um Transformationen auf Geometrie anzuwenden. Wenn wir zum Beispiel einen Punkt haben und ihn um eine Achse drehen wollen, nehmen wir eine Drehmatrix und multiplizieren sie mit dem Punkt, um den neuen Drehstandort zu erhalten.
$$\begin{array}{ccc} \text{Drehmatrix} & \text{Eingabepunkt} & \text{Drehpunkt}\\\begin{bmatrix}a & b & c & d \\e & f & g & h \\i & j & k & l \\0 & 0 & 0 & 1 \\\end{bmatrix}& \cdot\begin{bmatrix}x \\y\\z\\1 \\\end{bmatrix}&= \begin{bmatrix}x' \\y'\\z'\\1 \\\end{bmatrix}\end{array}$$Meistens müssen mehrere Transformationen auf derselben Geometrie ausgeführt werden. Wenn wir zum Beispiel tausend Punkte verschieben und drehen müssen, kann jegliche der folgenden Methoden zur Anwendung gebracht werden.
Methode 1
- Multiplizieren Sie die Verschiebungsmatrix mit 1000 Punkten, um die Punkte zu verschieben.
- Multiplizieren Sie die Drehmatrix mit den resultierenden 1000 Punkten, um die verschobenen Punkte zu drehen.
Zahl der Operationen = 2000.
Methode 2
- Multiplizieren Sie die Dreh- und Verschiebungsmatrices, um eine kombinierte Transformationsmatrix zu erhalten.
- Multiplizieren Sie die kombinierte Matrix mit 1000 Punkten, um Verschieben und Drehen in einem einzigen Schritt zu bewältigen.
Zahl der Operationen = 1001.
Beachten Sie, dass mit Methode 1 fast doppelt so viele Operationen benötigt werden, um das gleiche Ergebnis zu erzielen. Wenngleich Methode 2 sehr effizient ist, kann Sie nur angewendet werden, wenn sowohl die Verschiebungs- als auch Drehmatrices $$[4 \times 4]$$ sind. Aus diesem Grund wird in Computergrafiken eine $$[4 \times 4]$$-Matrix zur Darstellung aller Transformationen verwendet, und eine $$[4 \times 1]$$-Matrix zur Darstellung von Punkten.
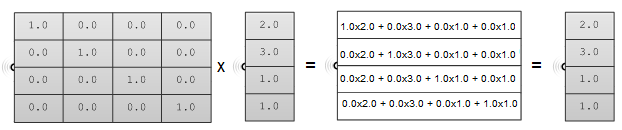
Dreidimensionale Modellierungsanwendungen enthalten Werkzeuge zum Transformieren und Multiplizieren von Matrices, wenn Sie jedoch an der mathematischen Multiplikation von Matrices interessiert sind, erklären wir Ihnen dies anhand eines einfachen Beispiels. Um zwei Matrices zu multiplizieren, müssen zunächst ihre Dimensionen übereinstimmen. Dies bedeutet, dass die Spaltenzahl in der ersten Matrix und die Zeilenzahl in der zweiten Matrix gleich sein müssen. Die Größe der resultierenden Matrix ergibt sich aus der Zeilenzahl der ersten Matrix und der Spaltenzahl der zweiten Matrix. Angenommen, wir haben zwei Matrices, $$M$$ und $$P$$, deren Dimensionen jeweils mit $$[4\times 4]$$ und $$[4 \times 1]$$ übereinstimmen, dann stimmt die Dimension der daraus resultierenden Multiplikationsmatrix $$M · P$$ mit $$[4 \times 1]$$ überein, wie in folgender Illustration zu sehen ist:
$$\begin{array}{ccc} M & P & P' \\\begin{bmatrix}\color{red}{a} & \color{red}{b} & \color{red}{c} & \color{red}{d} \\e & f & g & h \\i & j & k & l \\0 & 0 & 0 & 1 \\\end{bmatrix}& \cdot\begin{bmatrix}\color{red}{x} \\\color{red}{y} \\\color{red}{z} \\\color{red}{1} \\\end{bmatrix}&= \begin{bmatrix}\color{red}{x'=a*x+b*y+c*z+d*1}\\y'=e*x+f*y+g*z+h*1\\z'=i*x+j*y+k*z+l*1 \\1=0*x+0*y+0*z+1*1\\\end{bmatrix}\end{array}$$Einheitsmatrix
Die Einheitsmatrix ist eine spezielle Matrix, in der alle diagonalen Komponenten mit 1 gleich sind und der Rest mit 0.
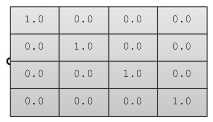
Die Haupteigenschaft der Einheitsmatrix ist, dass bei ihrer Multiplikation mit einer anderen Matrix die mit Null multiplizierten Werte nicht geändert werden.
2.2 Transformationsvorgänge
Die meisten Transformationen behalten die Parallelbeziehung der Geometrieteile zueinander bei. Kollineare Punkte zum Beispiel bleiben auch nach der Transformation kollinear. Auch Punkte auf einer Ebene bleiben nach der Transformation kollinear. Diese Art von Transformation wird auch affine Transformation genannt.
Transformation durch Transponieren (Verschieben)
Das Verschieben eines Punkts von einem Ausgangsstandort über einen bestimmten Vektor kann wie folgt berechnet werden:
$$P’ = P + \mathbf{\vec v}$$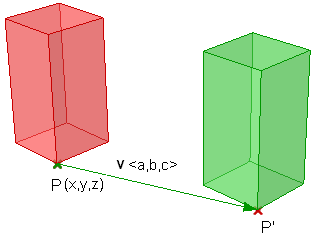
Nehmen wir an:
$$P(x,y,z)$$ ist ein gegebener Punkt
$$\mathbf{\vec v}=<a,b,c>$$ ist ein Transponierungsvektor
Daraus folgt:
$$P’(x) = x + a$$
$$P’(y) = y + b$$
$$P’(z) = z + c$$
Punkte werden in einem Matrixformat mittels einer [4x1]-Matrix dargestellt, mit einer in der letzten Zeile eingefügten 1. Der Punkt P(x,y,z) beispielsweise wird wie folgt dargestellt:
$$\begin{bmatrix}x\\y\\z\\1\\\end{bmatrix}$$Die Verwendung einer $$[4 \times 4]$$ -Matrix für Transformationen (was man ein homogenes Koordinatensystem nennt), anstatt von $$[3 \times 3]$$-Matrices, ermöglicht die Darstellung aller Transformationen einschließlich Transponierung. Das allgemeine Format für eine Transponierungsmatrix ist:
$$\begin{bmatrix}1 & 0 & 0 & \color{red}{a1} \\0 & 1 & 0 & \color{red}{a2} \\0 & 0 & 1 & \color{red}{a3} \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Um beispielsweise Punkt $$P(2,3,1)$$ über den Vektor $$\vec v <2,2,2>$$, zu verschieben, ist der neue Punktstandort:
$$P’ = P + \mathbf{\vec v} = (2+2, 3+2, 1+2) = (4, 5, 3)$$Wenn wir die Matrixform verwenden und die Transponierungsmatrix mit dem Eingabepunkt multiplizieren, erhalten wir den neuen Punktstandort wie nachfolgend:
$$\begin{bmatrix}1 & 0 & 0 & 2 \\0 & 1 & 0 & 2 \\0 & 0 & 1 & 2 \\0 & 0 & 0 & 1 \\\end{bmatrix}\cdot\begin{bmatrix}2 \\3\\1\\1 \\\end{bmatrix}= \begin{bmatrix}(1*2 + 0*3 + 0*1 + 2*1) \\(0*2 + 1*3 + 0*1 + 2*1)\\(0*2 + 0*3 + 1*1 + 2*1)\\(0*2 + 0*3 + 0*1 + 1*1)\\\end{bmatrix}=\begin{bmatrix}4 \\5\\3\\1 \\\end{bmatrix}$$In ähnlicher Weise wird jegliche Geometrie durch Multiplizieren ihrer Konstruktionspunkte mit der Transponierungsmatrix transponiert. Wenn wir zum Beispiel einen durch acht Eckpunkte definierten Quader haben und ihn 4 Einheiten weit in die x-Richtung, 5 Einheiten in die y-Richtung und 3 Einheiten in die z-Richtung verschieben wollen, müssen wir jeden der acht Quader-Eckpunkte mit folgender Transponierungsmatrix multiplizieren, um den neuen Quader zu erhalten.
$$\begin{bmatrix}1 & 0 & 0 & 4\\ 0 & 1 & 0 & 5 \\0 & 0 & 1 & 3 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$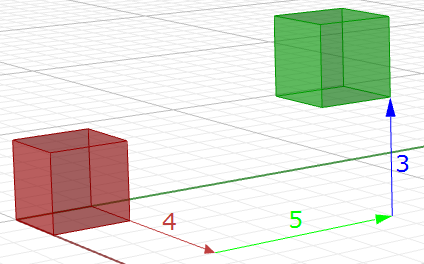
Drehtransformation
In diesem Abschnitt wird gezeigt, wie die Drehung um die z-Achse und den Ursprungspunkt mittels Trigonometrie berechnet wird, gefolgt von der Ableitung des allgemeinen Matrixformats für die Drehung.
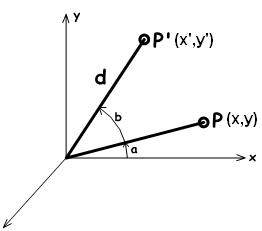
Nehmen Sie einen Punkt auf der $$x,y$$-Ebene $$P(x,y)$$ und drehen Sie ihn um den Winkel ( $$b$$). Anhand der Abbildung können wir Folgendes sagen:
$$x = d cos(a)$$ (1)
$$y = d sin(a)$$ (2)
$$x’ = d cos(b+a)$$ (3)
$$y’ = d sin(b+a)$$ (4)
Erweiterung von
$$x$$’ und
$$y’$$ mittels trigonometrischer Identitäten für den Sinus und Kosinus der Winkelsumme:
$$x’ = d cos(a)cos(b) - d sin(a)sin(b)$$ (5)
$$y’ = d cos(a)sin(b) + d sin(a)cos(b)$$ (6)
Mittels Eq 1 und 2:
$$x’ = x cos(b) - y sin(b)$$
y’ = x sin(b) + y cos(b)
Die Drehmatrix um die z-Achse sieht so aus:
$$\begin{bmatrix}\color{red}{\cos{b}} & \color{red}{-\sin{b}} & 0 & 0 \\\color{red}{\sin{b}} & \color{red}{\cos{b}} & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Die Drehmatrix um die x-Achse mit Winkel $$b$$ sieht so aus:
$$\begin{bmatrix}1 & 0 & 0 & 0 \\0 & \color{red}{\cos{b}} & \color{red}{-\sin{b}} & 0 \\0 & \color{red}{\sin{b}} & \color{red}{\cos{b}} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Die Drehmatrix um die y-Achse mit Winkel $$b$$ sieht so aus:
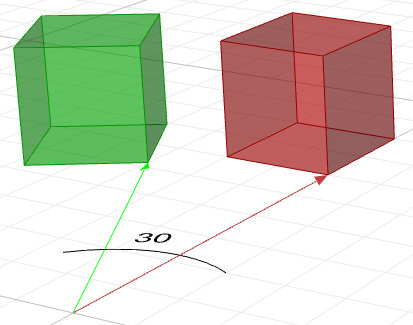
$$\begin{bmatrix}\color{red}{\cos{b}} &0 & \color{red}{\sin{b}} & 0 \\0 & 1 & 0 & 0 \\\color{red}{-\sin{b}} & 0 &\color{red}{\cos{b}} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Wenn wir zum Beispiel einen Quader haben und ihn um 30 Grad drehen wollen, ist folgendes zu tun:
1. Bilden Sie die 30-Grad-Drehmatrix. Bei Verwendung der allgemeinen Form sowie der cos- und sin-Werte des 30-Grad-Winkels wird die Drehmatrix so aussehen:
$$\begin{bmatrix}0.87 & -0.5 & 0 & 0 \\0.5 & 0.87 & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$2. Multiplizieren Sie die Drehmatrix mit der Eingabegeometrie, oder im Falle des Quaders, multiplizieren Sie mit jedem der Eckpunkte, um den neuen Quaderstandort zu finden.
Skalierungs-Transformation
Um Geometrie zu skalieren, brauchen wir einen Skalierungsfaktor und ein Skalierungszentrum. Der Skalierungsfaktor kann uniform sein, durch gleichmäßige Skalierung in x-, y- und z-Richtung, oder er kann für jede Dimension anders sein.
Zum Skalieren eines Punkts kann folgende Gleichung verwendet werden:
$$P’ = SkalierungsFaktor(S) * P$$
Oder:
$$P’.x = Sx * P.x$$
$$P’.y = Sy * P.y$$
$$P’.z = Sz * P.z$$
Dies ist das Matrixformat für die Skalierungs-Transformation, davon ausgehend, dass das Skalierungszentrum der Welt-Ursprungspunkt ist (0,0,0).
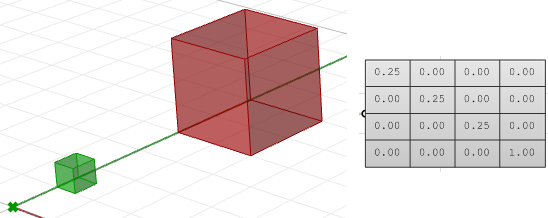
$$\begin{bmatrix}\color{red}{Skalierung-x} & 0 & 0 & 0 \\0 & \color{red}{Skalierung-y} & 0 & 0 \\0 & 0 & \color{red}{Skalierung-z} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Wenn wir beispielsweise einen Quader um 0.25 gegenüber des Weltursprungs skalieren möchten, sieht die Skalierungsmatrix wie folgt aus:
Scherungs-Transformation
Scherung in 3D wird entlang zweier Achsen in Bezug auf eine dritte Achse gemessen. Eine Scherung entlang einer z-Achse zum Beispiel ändert nicht die Geometrie entlang dieser Achse, sondern vielmehr entlang x und y. Hier sind einige Beispiele für Scherungsmatrices:
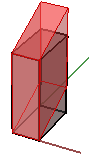
1. Scherung in x und z, bei Fixierung der y-Koordinate:
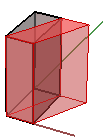$$\begin{bmatrix}1.0 &\color{red}{0.5} & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 &\color{red}{0.5} & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
2. Scherung in y und z, bei Fixierung der x-Koordinate:
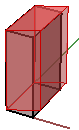$$\begin{bmatrix}1.0 & \color{red}{0.5} & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
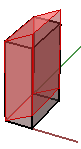$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & \color{red}{0.5} & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
3. Scherung in x und y, bei Fixierung der z-Koordinate:
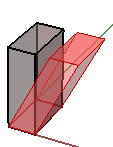$$\begin{bmatrix}1.0 & 0.0 & \color{red}{0.5} & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & \color{red}{0.5} & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
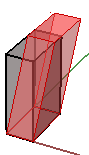
Spiegel- oder Reflektionstransformation
Die Spiegeltransformation erzeugt eine Reflektion eines Objekts über eine Linie oder Ebene hinweg. 2D-Objekte werden über eine Linie gespiegelt, 3D-Objekte hingegen über eine Ebene. Denken Sie daran, dass die Spiegeltransformation die Normalenrichtung der Geometrieseiten umkehrt.
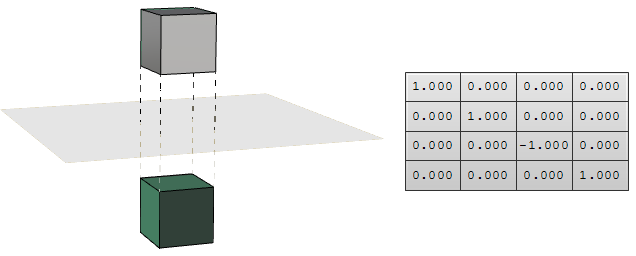
Planare Projektionstransformation
Rein intuitiv würde man sagen, der Projektionspunkt eines 3D-Punkts $$P(x,y,z)$$ auf der Welt-xy-Ebene ist gleichwertig mit $$P_{xy} (x,y,0)$$, womit der z-Wert auf Null gesetzt wird. Eine Projektion auf die xz-Ebene von Punkt P ist, in ähnlicher Weise, $$P_{xz}(x,0,z)$$. Wenn auf die yz-Ebene projiziert wird, $$P_{xz} = (0,y,z)$$. Diese werden orthogonale Projektionen genannt.
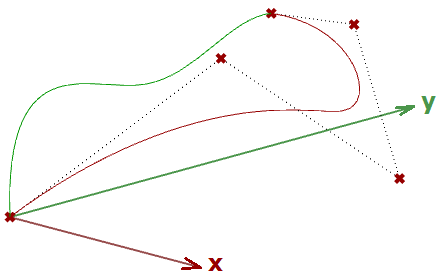
Wenn wir eine Kurve als Eingabe haben und die planare Projektionstransformation anwenden, erhalten wir eine auf diese Ebene projizierte Kurve. Im Folgenden sehen wir ein Beispiel einer auf die xy-Ebene projizierten Kurve mit dem Matrixformat.
Hinweis: NURBS-Kurven (die im nächsten Kapitel erklärt werden) verwenden Kontrollpunkte, um Kurven zu definieren. Die Projektion einer Kurve läuft auf die Projektion ihrer Kontrollpunkte hinaus.
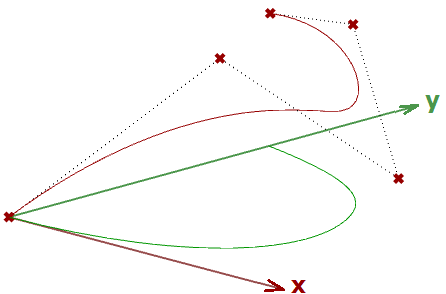$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & \color{red}{0.0} & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
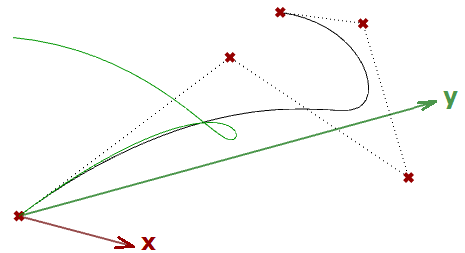$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & \color{red}{0.0} & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix} \color{red}{0.0} & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
Beispieldateien herunterladen
Laden Sie das Archiv download samplesand tutorials herunter, das alle Grasshopper-Beispiele und Codedateien in diesem Leitfaden enthält.
Weitere Schritte:
Jetzt, wo Sie mehr über Matrizen und Trasnformasion wissen, sollten Sie sich die Anleitung Parametrische Kurven und Flächen ansehen, um mehr über die detaillierte Struktur von NURBS-Kurven und -Flächen zu erfahren.
