Nehmen wir an, Sie legen jeden Werktag eine bestimmte Wegstrecke von Ihrer Wohnung zur Arbeit zurück. Sie gehen um 8:00 Uhr morgens aus dem Haus und kommen um 9:00 Uhr an. Jeden Augenblick zwischen 8:00 und 9:00 Uhr wären Sie an irgendeinem Punkt des Weges. Wenn Sie unterwegs jede Minute ihre jeweilige Position aufzeichnen, können Sie die Wegstrecke von der Wohnung zur Arbeit durch einfaches Verbinden Ihrer 60 aufgezeichneten Punkte bestimmen. Vorausgesetzt, Sie legen diese Wegstrecke jeden Tag mit genau der gleichen Geschwindigkeit zurück, wären Sie um 8:00 Uhr noch zu Hause (Ausgangspunkt), um 9:00 Uhr wären Sie auf der Arbeit (Endpunkt) und um 8:40 wären Sie genau an der mit dem 40. Aufzeichnungspunkt übereinstimmenden Wegposition. Glückwunsch, hiermit haben Sie Ihre erste parametrische Kurve definiert! Sie haben Zeit als einen Parameter zur Bestimmung Ihrer Wegstrecke verwendet, weswegen Sie Ihre Pfadkurve als parametrische Kurve bezeichnen können. Der von Beginn bis Ende benötigte Zeitraum (8 bis 9) wird Kurvendomäne oder Intervall genannt.
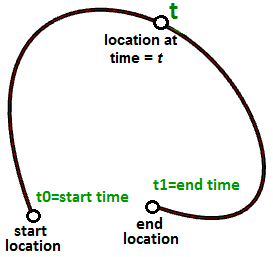
Im Allgemeinen können wir die Standorte
$$x$$,
$$y$$ und
$$z$$ einer parametrischen Kurve im Hinblick auf einen Parameter
$$t$$ wie folgt beschreiben:
$$x = x(t)$$
$$y = y(t)$$
$$z = z(t)$$
Wobei:
$$t$$ eine Auswahl reeller Zahlen ist
Wir haben bereits gesehen, dass die parametrische Gleichung einer Linie hinsichtlich Parameter $$t$$ definiert wird als:
$$x = x’ + t * a$$
$$y = y’ + t * b$$
$$z = z’ + t * c$$
Wobei:
$$x$$,
$$y$$ und
$$z$$ Funktionen von t sind und t eine Auswahl reeller Zahlen repräsentiert.
$$x’$$,
$$y’$$ und
$$z’$$ sind die Koordinaten eines Punktes auf dem Linienabschnitt.
$$a$$,
$$b$$ und
$$c$$ die Neigung der Linie bestimmen, so dass der Vektor
$$\mathbf{\vec v} <a, b, c>$$ parallel zur Linie ist.
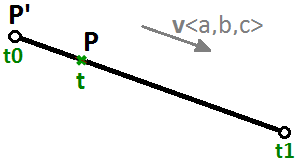
Daher können wir die parametrische Gleichung eines Liniensegments unter Verwendung eines $$t$$-Parameters schreiben, der sich zwischen zwei reellen Zahlenwerten $$t0$$, $$t1$$ und einem Einheitsvektor $$\mathbf{\vec v}$$ bewegt, der wie folgt in der Linienrichtung liegt:
$$P = P’ + t * \mathbf{\vec v}$$Ein weiteres Beispiel ist ein Kreis. Die parametrische Gleichung des Kreises auf der xy-Ebene mit einem Zentrum auf dem Ursprung (0,0) und einem Winkelparameter $$t$$ zwischen $$0$$ und $$2π$$ Bogenmaß ist:
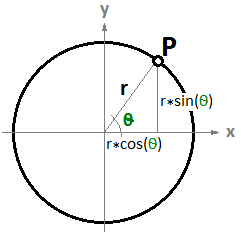
$$x = r \dot cos(t)$$
$$y = r \dot sin(t)$$
Wir können die allgemeine Gleichung eines Kreises für die parametrische Gleichung wie folgt ableiten:
$$ x/r = cos(t)$$
$$y/r = sin(t)$$
Und weil:
$$cos(t)^2 + sin(t)^2 = 1$$ (Pythagoreische Identität)
Daraus folgt:
$$(x/r)^2 + (y/r)^2 = 1$$ , or
$$x^2 + y^2 = r^2$$
3.1 Parametrische Kurven
Kurvenparameter
Ein Parameter auf einer Kurve repräsentiert die Adresse eines Punkts auf dieser Kurve. Wie bereits erwähnt, kann man sich die parametrische Kurve als einen innerhalb einer bestimmten Zeit zurückgelegten Weg zwischen zwei Punkten vorstellen, dies mit einer festgelegten oder variablen Geschwindigkeit. Wenn für die Wegstrecke der Zeitraum $$T$$ benötigt wird, dann repräsentiert der Parameter t eine Zeit innerhalb von $$T$$, welche als ein Standort (Punkt) auf der Kurve erscheint.
Wenn man einen geraden Weg (Streckenabschnitt) zwischen den beiden Punkten $$A$$ und $$B$$ hat, und $$\mathbf{\vec v}$$ ein Vektor von $$A$$ nach $$B$$ ( $$\mathbf{\vec v} = B - A$$) wäre, dann kann man die parametrische Geradengleichung verwenden, um alle Punkte $$M$$ zwischen $$A$$ und $$B$$ wie folgt zu finden:
$$M = A + t*(B-A)$$
Wobei:
$$t$$ ein Wert zwischen 0 und 1 ist.
Auf den Bereich der t-Werte, 0 bis 1 in diesem Fall, wird als Kurvendomäne oder Intervall Bezug genommen. Wäre t ein Wert außerhalb der Domäne (weniger als 0 oder mehr als 1), dann verbleibt der resultierende Punkt $$M$$ außerhalb der linearen Kurve $$\overline{AB}$$.
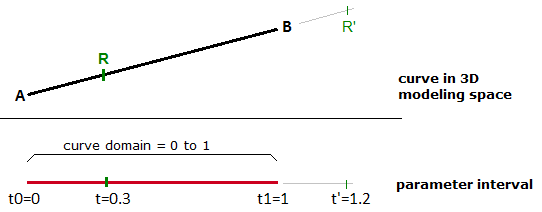
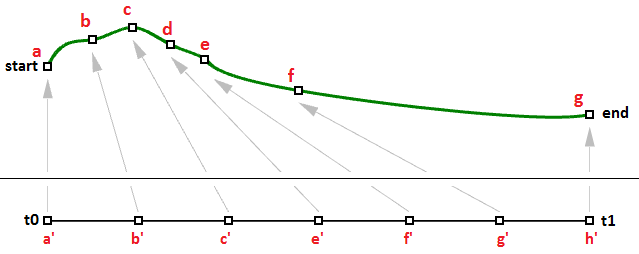
Das gleiche Prinzip ist auf jegliche parametrische Kurve anwendbar. Jeder Punkt auf der Kurve kann unter Verwendung des Parameters t innerhalb des Intervalls oder der Domäne derjenigen Werte berechnet werden, welche die Begrenzungen der Kurve bestimmen. Auf den Startparameter dieser Domäne wird gewöhnlich als $$t0$$ Bezug genommen, und auf das Ende der Domäne als $$t1$$.
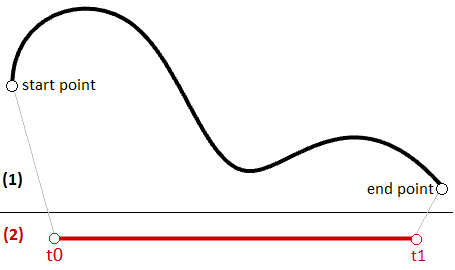
Kurvendomäne oder Intervall
Eine Kurvendomäne oder Intervall wird definiert als der Bereich von Parametern, die zu einem Punkt innerhalb dieser Kurve ausgewertet werden. Die Domäne wird gewöhnlich mit zwei reellen Zahlen beschrieben, welche die in der Form (min bis max) oder (min, max) ausgedrückten Domänenbeschränkungen definieren. Die Domänenbeschränkungen können zwei beliebige Werte sein, die auf die tatsächliche Länge der Kurve bezogen sein können oder auch nicht. In einer ansteigenden Domäne wird der Parameter der min-Domäne zum Startpunkt der Kurve ausgewertet, und max-Domäne zum Endpunkt der Kurve.
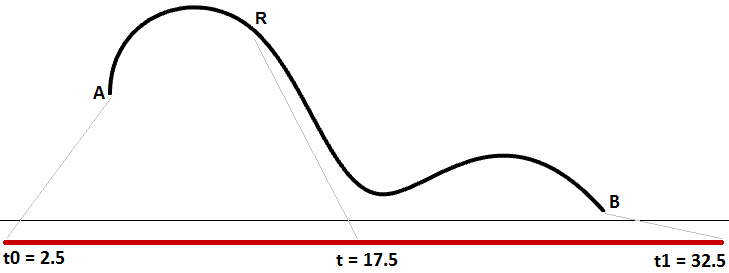
Auf die Änderung einer Kurvendomäne wird als Vorgang der Reparametrisierung der Kurve Bezug genommen. Es ist zum Beispiel sehr häufig der Fall, dass die Domäne auf (0 bis 1) geändert wird. Die Reparametrisierung einer Kurve wirkt sich nicht auf die Form der 3D-Kurve aus. Sie ist vergleichbar mit der Änderung der Wegzeit durch Laufen statt Gehen, wodurch die Form des Weges nicht verändert wird.
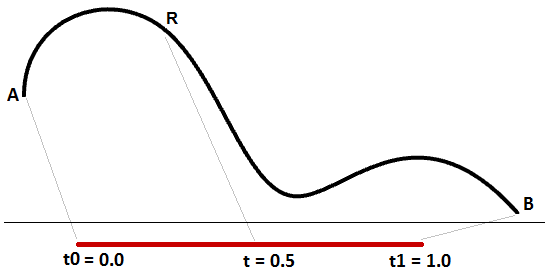
Eine ansteigende Domäne bedeutet, dass der Minimalwert der Domäne zum Kurvenanfang weist. Üblicherweise, jedoch nicht immer, sind Domänen ansteigend.
Kurvenauswertung
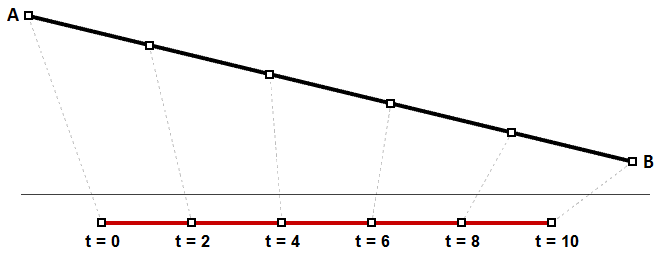
Wir haben gelernt, dass es sich bei einem Kurvenintervall um den Bereich aller Parameterwerte handelt, die zu Punkten innerhalb der 3D-Kurve ausgewertet werden. Es besteht jedoch keinerlei Garantie, dass beispielsweise die Auswertung auf der Mitte der Domäne einen Punkt in der Mitte der Kurve ergibt, wie in Abb. (29) zu sehen.
Die gleichförmige Parametrisierung einer Kurve können wir uns vorstellen, als würden wir eine Wegstrecke mit konstanter Geschwindigkeit zurücklegen. Eine Linie von Grad 1 zwischen zwei Punkten wäre ein Beispiel, bei dem gleiche Intervalle oder Parameter gleiche Intervalle einer Bogenlänge auf der Linie ergeben. In diesem speziellen Fall werden gleiche Intervalle von Parametern zu gleichen Intervallen auf der 3D-Kurve ausgewertet.
Es ist allerdings wahrscheinlicher, dass die Geschwindigkeit entlang der Wegstrecke ab- oder zunimmt. Wenn etwa zum Zurücklegen einer Wegstrecke 30 Minuten benötigt werden, ist es dennoch unwahrscheinlich, dass Sie bei Minute 15 genau die Hälfte des Wegs bewältigt haben. Abb. (30) zeigt einen typischen Fall, in dem gleiche Parameterintervalle zu variablen Längen auf der 3D-Kurve ausgewertet werden.
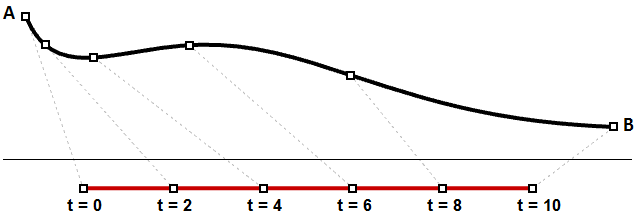
Möglicherweise müssen Sie Punkte auf einer 3D-Kurve auswerten, die sich auf einer prozentuell definierten Position der Kurvenlänge befinden. Es kann zum Beispiel sein, dass Sie die Kurve in gleiche Längen teilen müssen. 3D-Modellierer sind normalerweise mit Werkzeugen zur Auswertung von Kurven relativ zur Bogenlänge ausgestattet.
Tangentialvektor zu einer Kurve
Eine Tangente zu einer Kurve auf einem beliebigen Parameter (oder Punkt auf einer Kurve) ist der Vektor, der die Kurve auf diesem Punkt trifft, aber nicht darüber hinausgeht. Die Neigung des Tangentialvektors ist mit der Neigung der Kurve am selben Punkt gleichwertig. Im folgenden Beispiel wird die Tangente zu einer Kurve auf zwei verschiedenen Parametern ausgewertet.
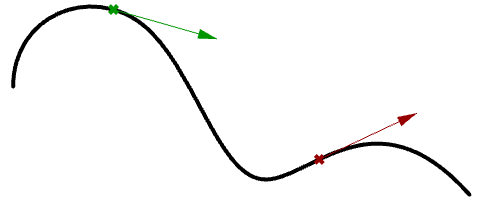
Kubische Polynomkurven
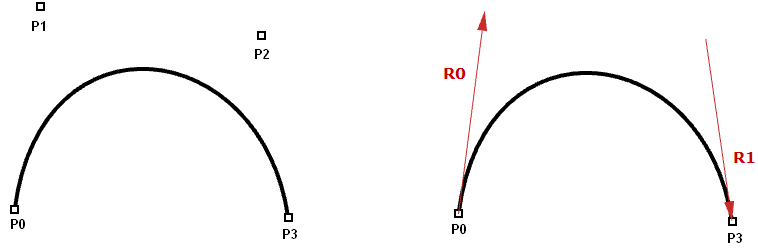
Hermite- und Bézier-Kurven sind zwei Beispiele kubischer Polynomkurven, die durch vier Parameter bestimmt werden. Eine Hermite-Kurve wird durch zwei Endpunkte bestimmt sowie zwei Tangentialvektoren auf diesen Punkten, während eine Bézier-Kurve durch vier Punkte bestimmt wird. Während sie mathematisch Unterschiede aufweisen, haben Sie doch ähnliche Eigenschaften und Einschränkungen.
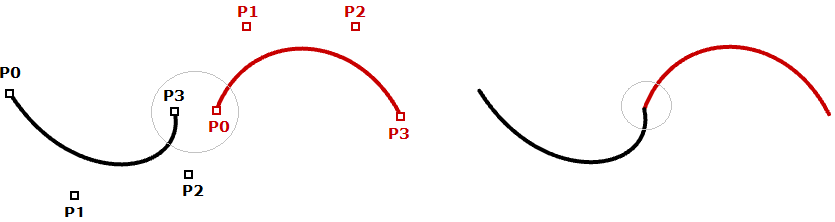
In den meisten Fällen bestehen Kurven aus mehreren Segmenten. Dies erfordert die Erstellung dessen, was man eine stückweise kubische Kurve nennt. In dieser Illustration verwendet eine stückweise Bézier-Kurve 7 Speicherpunkte zur Erzeugung einer kubischen Zweisegmentkurve. Beachten Sie dass die Endkurve, wenngleich sie verbunden ist, nicht glatt oder durchgehend aussieht.
Obwohl Hermite-Kurven die gleiche Zahl von Parametern verwenden wie Bézier-Kurven (vier Parameter zum Definieren einer Kurve), bieten Sie die zusätzlichen Informationen der Tangentialkurve, die auch mit dem nächsten Stück geteilt werden kann, und zwar zur Erzeugung einer glatter aussehenden Kurve mit weniger Gesamtspeicherung, wie im Folgenden zu sehen ist.
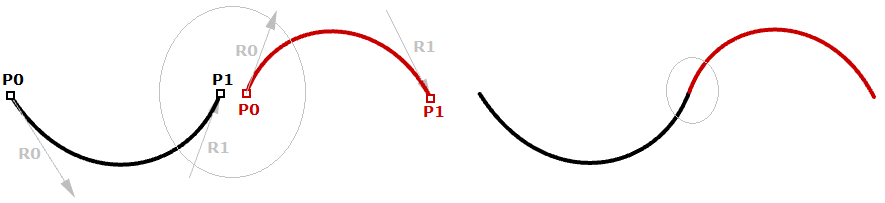
Der nicht-uniforme rationale B-Spline (NURBS) ist eine vielfach anwendbare Kurvendarstellung, die sich auch für glattere und durchgängigere Kurven eignet. Segmente teilen mehr Kontrollpunkte für den Erhalt noch glatterer Kurven mit weniger Speicherung.
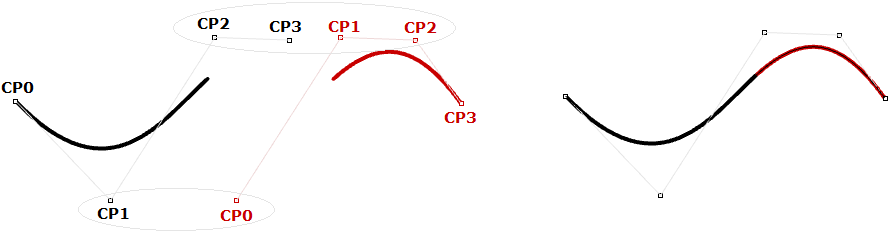
NURBS-Kurven und -Flächen sind die vorrangigen mathematischen Darstellungen, die Rhino zur Geometriedarstellung verwendet. Auf die Eigenschaften und Komponenten von NURBS-Kurven wird im weiteren Verlauf des Kapitels noch etwas näher eingegangen.
Auswertung kubischer Bézier-Kurven
Der nach seinem Erfinder Paul de Casteljau benannte De-Casteljau-Algorithmus wertet Bézier-Kurven unter Verwendung einer rekursiven Methode aus. Die Schritte des Algorithmus können wie folgt zusammengefasst werden:
Eingabe:
Vier Punkte $$A$$, $$B$$, $$C$$, $$D$$ definieren eine Kurve $$t$$, ist ein beliebiger Parameter innerhalb einer Kurvendomäne
Ausgabe:
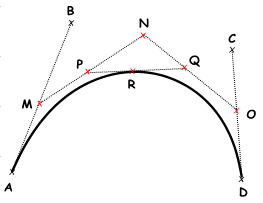
Punkt $$R$$ auf der Kurve auf dem Parameter $$t$$.
Lösung:
- Finden Sie Punkt
$$M$$ an Parameter
$$t$$ auf der Linie
$$$\overline{AB}$$.
2.Finden Sie Punkt $$N$$ an Parameter $$t$$ auf der Linie $$\overline{BC}$$.
3.Finden Sie Punkt $$O$$ an Parameter $$t$$ auf der Linie $$\overline{CD}$$.
4.Finden Sie Punkt $$P$$ an Parameter $$t$$ auf der Linie $$\overline{MN}$$.
5.Finden Sie Punkt $$Q$$ an Parameter $$t$$ auf der Linie $$$\overline{NO}$$.
6.Finden Sie Punkt $$R$$ an Parameter $$t$$ auf der Linie $$\overline{PQ}$$.
3.2 NURBS-Kurven
NURBS ist eine genaue mathematische Darstellung von Kurven, deren Bearbeitung sehr intuitiv geschieht. Freiformkurven können leicht unter Verwendung von NURBS dargestellt werden, und dank der Kontrollstruktur ist eine leichte und vorhersagbare Bearbeitung möglich.
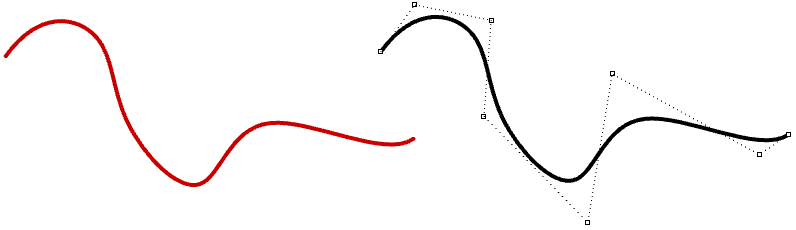
Wenn Sie an tiefergehender Lektüre über NURBS interessiert sind, steht Ihnen eine Vielzahl von Büchern und Referenzen zur Verfügung. Ein grundlegendes Verständnis von NURBS ist in jedem Fall notwendig, um einen NURBS-Modellierer effektiver nutzen zu können. Es gibt vier Hauptattribute, die eine NURBS-Kurve definieren: Grad, Kontrollpunkte, Knoten und Bewertungsregeln.
Grad
Der Kurvengrad ist eine ganze positive Zahl. Rhino ermöglicht das Arbeiten mit jeglicher Gradkurve, beginnend bei 1. Die Grade 1, 2, 3 und 5 sind die nützlichsten, Grad 4 und alle über Grad 5 hingegen finden in der wirklichen Welt wenig Anwendung. Es folgen einige Beispiele für Kurven und ihren Grad:
| Linien und Polylinien sind NURBS-Kurven ersten Grades. | 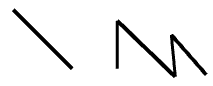 |
| Kreise und Ellipsen sind Beispiele für NURBS-Kurven zweiten Grades. |  |
| Freiform-Kurven werden gewöhnlich als NURBS-Kurven dritten oder fünften Grades dargestellt. |
 |
Kontrollpunkte
Die Kontrollpunkte einer NURBS-Kurve ist eine Liste von (Grad+1)-Punkten. Die intuitivste Methode, die Form einer NURBS-Kurve zu verändern, besteht in der Verschiebung ihrer Kontrollpunkte.
Die Anzahl der Kontrollpunkte, die sich auf das jeweilige Segment einer NURBS-Kurve auswirken, wird durch den Kurvengrad bestimmt. Beispielsweise unterliegt das jeweilige Segment in einer Kurve ersten Grades lediglich der Auswirkung der beiden End-Kontrollpunkte. In einer Kurve zweiten Grades wirken sich drei Kontrollpunkte auf das jeweilige Segment aus, und so weiter.
| Kontrollpunkte von Kurven ersten Grades gehen durch alle Kurvenkontrollpunkte. In einer NURBS-Kurve ersten Grades bestimmen zwei (Grad+1)-Kontrollpunkte jedes Segment. Bei Verwendung von fünf Kontrollpunkten hat die Kurve vier Segmente. | 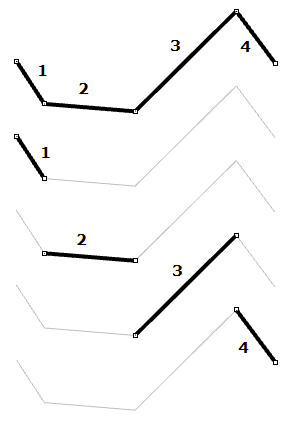 |
| Kreise und Ellipsen sind Beispiele für Kurven zweiten Grades. In einer NURBS-Kurve zweiten Grades bestimmen drei (Grad+1)-Kontrollpunkte das jeweilige Segment. Bei Verwendung von fünf Kontrollpunkten hat die Kurve drei Segmente. | 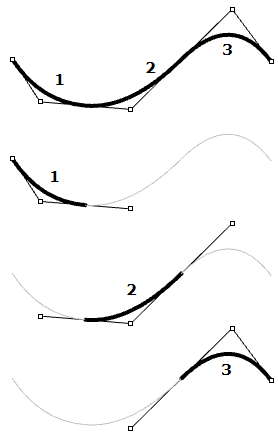 |
| Kontrollpunkte für Kurven dritten Grades berühren normalerweise nicht die Kurve, außer an Endpunkten in offenen Kurven. In einer NURBS-Kurve dritten Grades bestimmen vier (Grad+1)-Kontrollpunkte das jeweilige Segment. Bei Verwendung von fünf Kontrollpunkten hat die Kurve zwei Segmente | 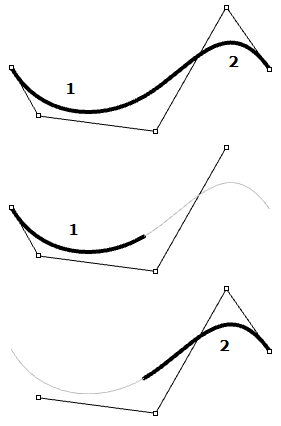 |
Wichtungen von Kontrollpunkten
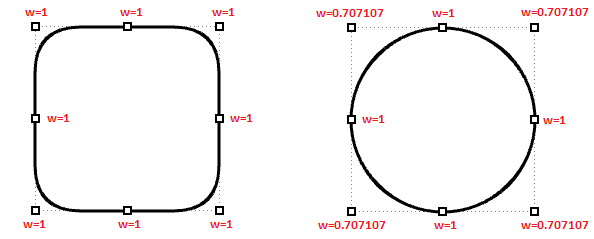
Jeder Kontrollpunkt hat eine angegliederte Zahl, die Wichtung genannt wird. Bis auf wenige Ausnahmen sind Wichtungen positive Zahlen. Wenn alle Kontrollpunkte dieselbe Wichtung haben, normalerweise 1, wird die Kurve nicht-rational genannt. Intuitiv sind die Wichtungen denkbar als die Schwere jedes einzelnen Kontrollpunkts. Je höher die relative Wichtung eines Kontrollpunkts, desto näher wird die Kurve an diesen Kontrollpunkt herangezogen.
Anzumerken ist, dass das Ändern von Kurvenwichtungen am besten vermieden werden sollte. Wichtungen zu ändern erbringt selten das gewünschte Resultat, wogegen es viele Herausforderungen hinsichtlich der Berechnung z.B. von Überschneidungen mit sich bringt. Der einzige hinreichende Grund für die Verwendung rationaler Kurven ist die Darstellung von Kurven, die anders nicht gezeichnet werden können, zum Beispiel Kreise und Ellipsen.
Knoten
Jede NURBS-Kurve hat eine Liste daran angegliederter Zahlen, genannt Knotenliste (und gelegentlich mit dem Begriff Knotenvektor bezeichnet). Knoten sind etwas schwerer zu verstehen und einzustellen. Bei Verwendung eines 3D-Modellierers müssen die Knoten nicht für jede erzeugte Kurve von Hand eingestellt werden; ein paar nützliche Dinge können wir über Knoten trotzdem lernen.
Knoten als Parameterwerte
Knoten sind eine nicht-absteigende Liste von Parameterwerten, die innerhalb der Kurvendomäne liegen. In Rhino gibt es Grad-1 mehr Knoten als Kontrollpunkte. Das heißt, die Anzahl der Knoten ist gleich wie die Anzahl der Kontrollpunkte plus Grad der Kurve minus 1:
|Knoten| = |CVs| + Grad - 1
Normalerweise sind für nicht-periodische Kurven die Knoten des ersten Grades gleich wie das Domäne-Minimum, und die Knoten des letzten Grades sind gleich wie das Domäne-Maximum.
Zum Beispiel können viele Knoten einer offenen NURBS-Kurve dritten Grades mit 7 Kontrollpunkten und einer Domäne zwischen 0 und 4 aussehen wie <0, 0, 0, 1, 2, 3, 4, 4, 4>.
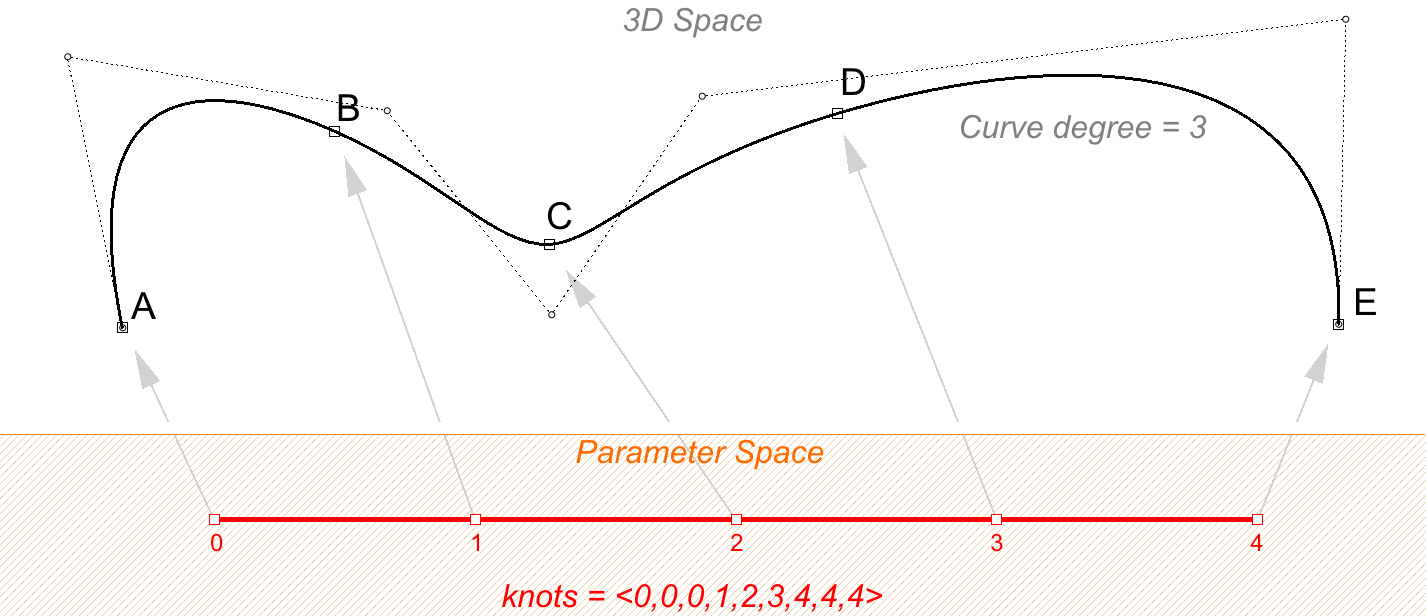
Die Skalierung einer Knotenliste wirkt sich nicht auf die 3D-Kurve aus. Wenn Sie die Domäne der Kurve im obigen Beispiel von “0 bis 4” auf “0 bis 1” ändern, wird die Knotenliste skaliert, aber die 3D-Kurve ändert sich nicht.
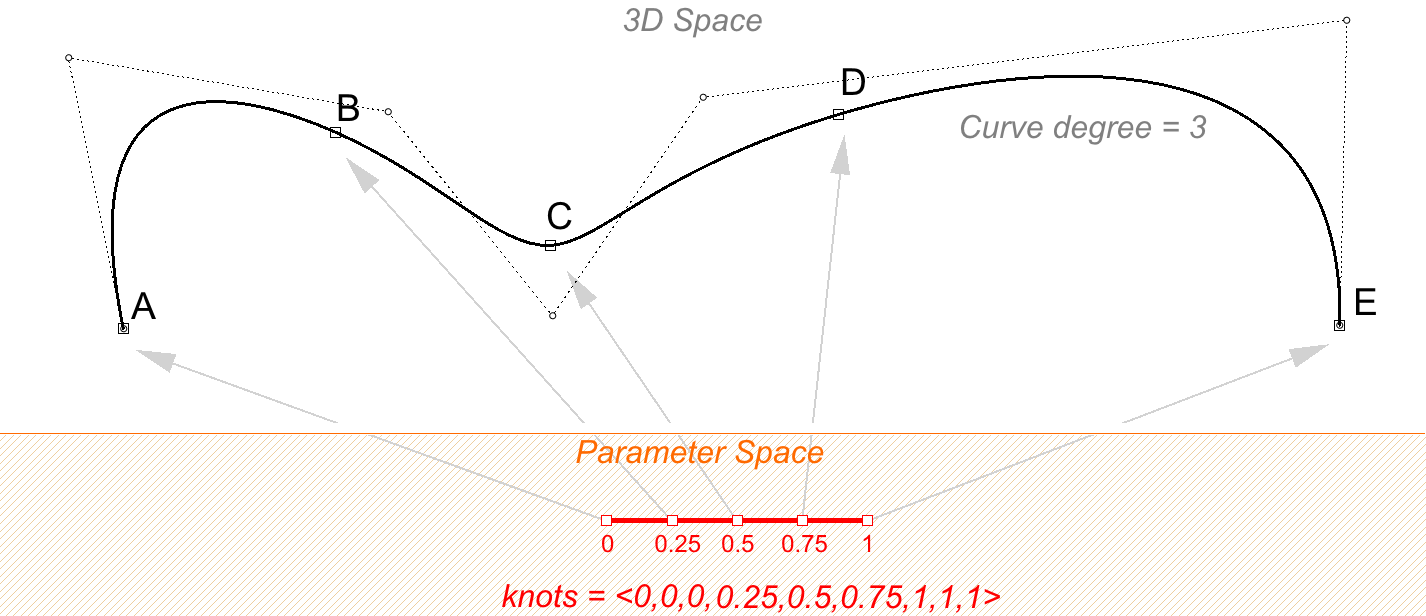
Einen Knoten mit Wert, der nur einmal erscheint, nennen wir einen Einfachen Knoten. Innere Knoten sind meistens einfach, wie in den beiden Beispielen oben.
Knotenvielfalt
Die Vielfalt eines Knoten ist die Häufigkeit, mit der er in der Knotenliste aufgelistet ist. Die Vielfalt eines Knoten kann nicht höher sein als der Grad der Kurve. Knotenvielfalt wird verwendet, um die Stetigkeit am jeweiligen Kurvenpunkt zu steuern.
Vollständige Mehrfachknoten
Ein vollständiger Mehrfachknoten hat die gleiche Vielfalt wie der Kurvengrad. Auf einem vollständigen Mehrfachknoten gibt es einen entsprechenden Kontrollpunkt, und die Kurve geht durch diesen Punkt.
Eingespannte oder offene Kurven haben zum Beispiel Knoten mit vollständiger Mehrfachkeit an den Enden der Kurve. Aus diesem Grund stimmen die End-Kontrollpunkte mit den Kurven und Punkten überein. Innere vollständige Mehrfachknoten ermöglichen einen Knick in der Kurve am entsprechenden Punkt.
Die folgenden beiden Kurven sind zum Beispiel dritten Grades und haben die gleiche Anzahl und den gleichen Standort wie die Kontrollpunkte. Sie haben jedoch verschiedene Knoten, und ihre Form ist ebenfalls verschieden. Vollständige Mehrfachkeit zwingt die Kurve durch den angegliederten Kontrollpunkt.
Hier sehen Sie zwei Kurven mit gleichem Grad, sowie gleicher Anzahl und Position der Kontrollpunkte, die jedoch unterschiedliche Knotenvektoren haben, was zu einer unterschiedlichen Kurvenform führt:
| Degree = 3 Anzahl der Kontrollpunkte = 7 knots = <0,0,0,1,2,3,4,4,4> = 9 knots Domäne (0 bis 4) |
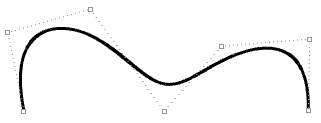 |
| Degree = 3 Anzahl der Kontrollpunkte = 7 knots = <0,0,0,1,1,1,4,4,4> = 9 knots Domäne (0 bis 4) Hinweis: Ein vollständiger Mehrfachknoten in der Mitte erzeugt einen Knick und die Kurve wird durch den angegliederten Kontrollpunkt gezwungen. |
 |
Gleichförmige Knoten
Eine gleichförmige Liste von Knoten erfüllt folgende Bedingung:
Knoten beginnen mit einem vollständigen Mehrfachknoten, gefolgt von einfachen Knoten, und enden mit einem vollständigen Mehrfachknoten. Die Werte sind aufsteigend und in gleichmäßigen Abständen angeordnet. Dies ist typisch für eingespannte oder offene Kurven. Periodische Kurven funktionieren anders, wie wir noch sehen werden.
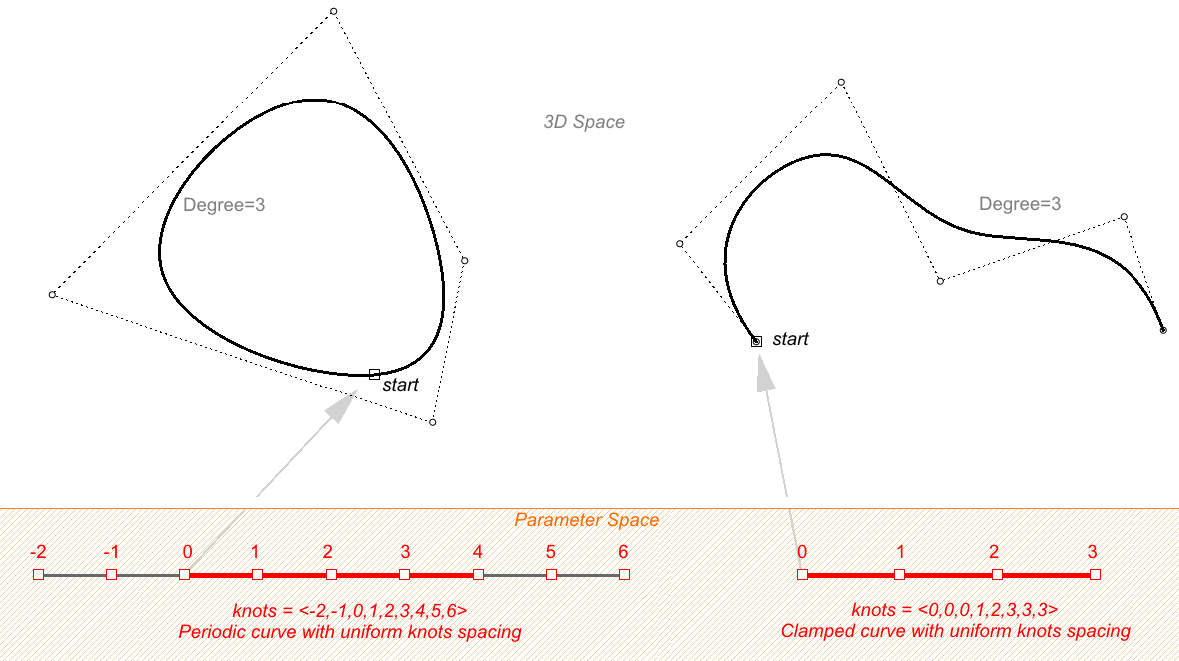
Nicht gleichförmige Knoten
NURBS-Kurven dürfen nicht-gleichförmige Abstände zwischen Knoten haben. Dies kann bei der Steuerung der Krümmung entlang der Kurve hilfreich sein, um mehr glatte Kurven zu erzeugen. Nehmen Sie folgendes Beispiel zur Interpolierung durch Punkte unter Verwendung einer Liste nicht-gleichförmiger Knoten auf der linken und gleichförmiger Knoten auf der rechten Seite. Wenn die Knotenabstände einer NURBS-Kurve proportional zu den Abständen zwischen Kontrollpunkten sind, ist die Kurve im Allgemeinen glatter.
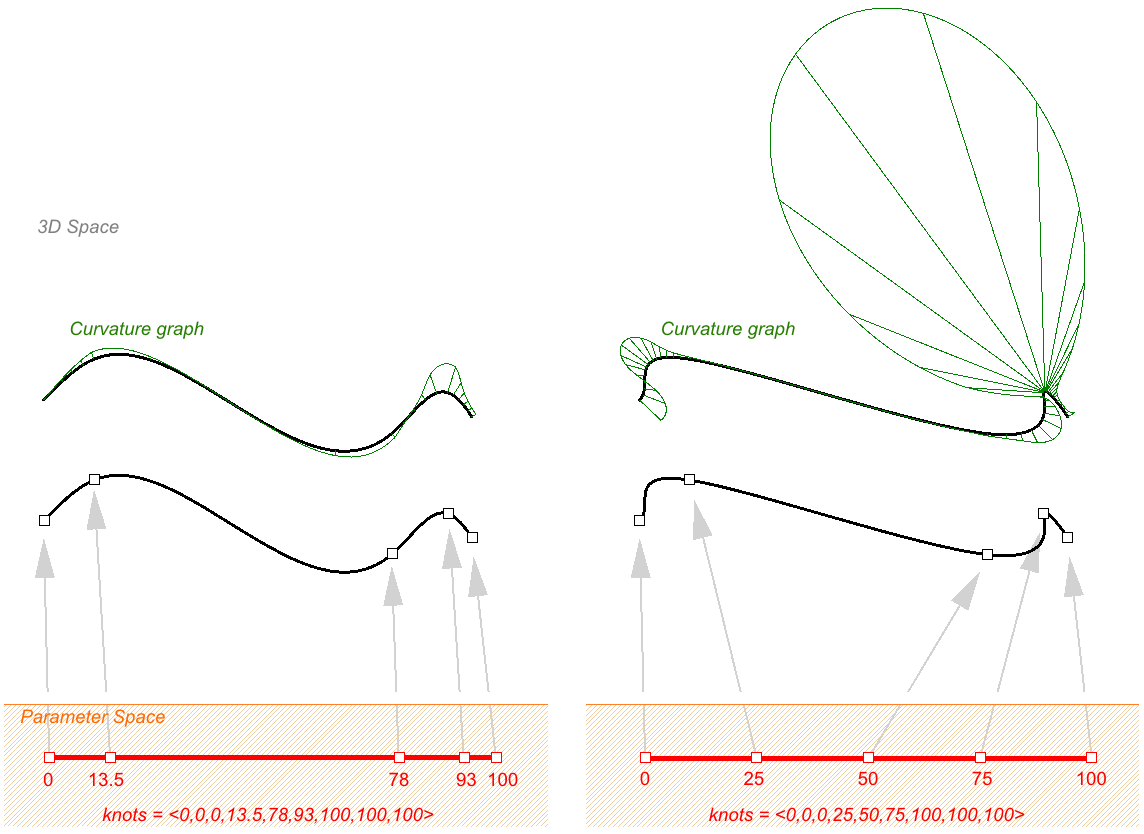
Ein Beispiel für eine Kurve, die sowohl nicht-gleichförmig als auch rational wäre, ist ein NURBS-Kreis. Die folgende ist eine Kurve zweiten Grades mit 9 Kontrollpunkten und 10 Knoten. Domäne ist 0-4, und die Abstände variieren zwischen 0 und 1. knots = <0,0,1,1,2,2,3,3,4,4> — (full multiplicity in the interior knots) Abstände zwischen Knoten = [0,1,0,1,0,1,0,1,0] — (nicht-gleichförmig)
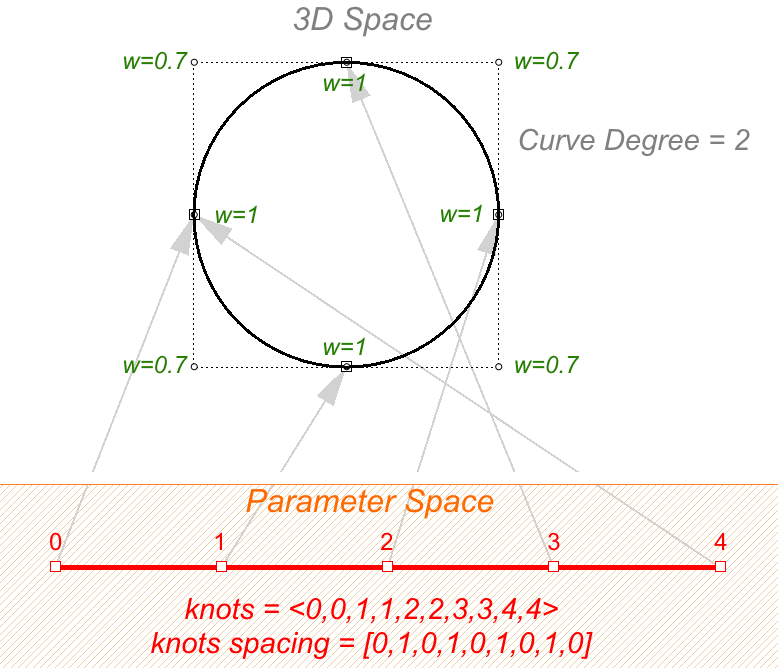
Auswertungsregel
Die Auswertungsregel verwendet eine mathematische Formel, die eine Zahl innerhalb der Kurvendomäne nimmt und einen Punkt zuordnet. Die Formel berücksichtigt Grad, Kontrollpunkte und Knoten.
Unter Verwendung dieser Formel können spezialisierte Kurvenfunktionen einen Kurvenparameter nehmen und den entsprechenden Punkt auf dieser Kurve erzeugen. Ein Parameter ist eine Zahl, die innerhalb der Kurvendomäne liegt. Domänen sind in der Regel ansteigend und bestehen aus zwei Zahlen: dem minimalen Domänenparameter $$t(0)$$, der den Anfangspunkt der Kurve auswertet und dem maximalen $$t(1)$$, der den Endpunkt der Kurve auswertet.
Eigenschaften von NURBS-Kurven
Um eine NURBS-Kurve zu erzeugen müssen Sie folgende Informationen erteilen:
- Bemaßung, üblicherweise 3
- Grad, (manchmal mittels der Größenordnung, die Grad+1 entspricht)
- Kontrollpunkte (Liste von Punkten)
- Wichtung der Kontrollpunkte (Liste von Zahlen)
- Knoten (Liste von Zahlen)
Wenn Sie eine Kurve erzeugen, müssen Sie mindestens den Grad und die Standorte der Kontrollpunkte bestimmen. Alle weiteren zur Erzeugung von NURBS-Kurven notwendigen Informationen können automatisch erstellt werden. Durch die Auswahl eines Endpunkts zur Übereinstimmung mit dem Anfangspunkt würde üblicherweise eine periodische, glatte geschlossene Kurve erzeugt werden. Die folgende Tabelle enthält Beispiele offener und geschlossener Kurven:
| Offene Kurve ersten Grades. Die Kurve verläuft durch alle Kontrollpunkte. |
 |
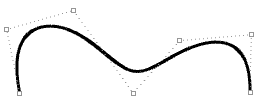
| Offene Kurve dritten Grades. Beide Kurvenenden stimmen mit Endkontrollpunkten überein. |
 |
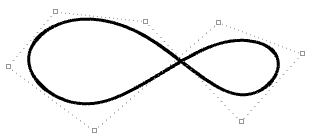
| Geschlossene periodische Kurve dritten Grades. Die Kurvennaht geht nicht durch einen Kontrollpunkt. |
 |
| Das Verschieben von Kontrollpunkten einer periodischen Kurve wirkt sich nicht auf die Kurvenglätte aus. | 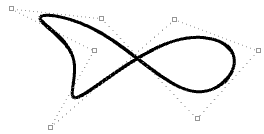 |
| Knicke entstehen, wenn die Kurve durch einige Kontrollpunkte gezwungen wird. | 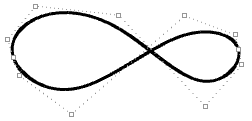 |
| Das Verschieben der Kontrollpunkte einer nicht periodischen Kurve garantiert keine glatte Kurvenstetigkeit, verschafft jedoch mehr Kontrolle über das Ergebnis. | 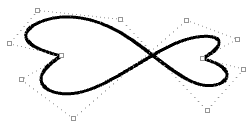 |
Eingespannte im Vergleich zu periodischen NURBS-Kurven
Die Endpunkte geschlossener eingespannter Kurven stimmen mit End-Kontrollpunkten überein. Periodische Kurven sind glatte geschlossene Kurven. Die Unterschiede zwischen beiden sind am besten anhand eines Vergleichs der Kontrollpunkte und Knoten zu verstehen.
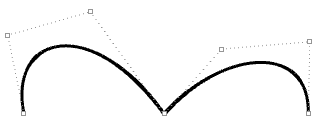
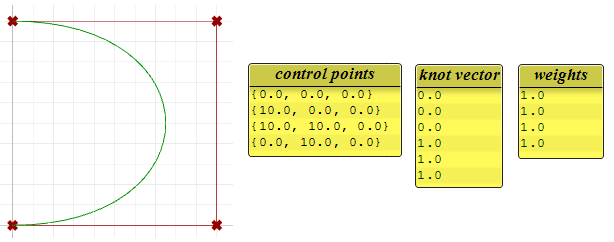
Was folgt, ist ein Beispiel einer offenen, eingespannten, nicht-rationalen NURBS-Kurve. Diese Kurve hat vier Kontrollpunkte, gleichförmige Knoten mit vollständiger Mehrfachkeit an den Anfangs- und Endknoten und den Wichtungen gleich 1.

Die folgende kreisförmige Kurve ist ein Beispiel einer geschlossenen, periodischen NURBS-Kurve dritten Grades. Ebenso ist sie nicht-rational, da alle Wichtungen gleich sind. Beachten Sie, dass die periodischen Kurven mehr Kontrollpunkte mit wenig Überlappung benötigen. Auch sind die Knoten einfach.
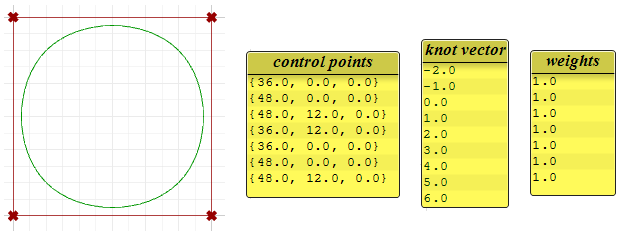
Beachten Sie, dass die periodische Kurve die vier Eingabepunkte in sieben Kontrollpunkte (Grad+4) umgewandelt hat, während die eingespannte Kurve nur die vier Kontrollpunkte verwendete. Die Knoten der periodischen Kurve verwenden einfache Knoten, während die Anfangs- und Endknoten der eingespannten Kurve vollständige Mehrfachkeit haben, womit die Kurve durch die Anfangs- und Endkontrollpunkte gezwungen wird.
Wenn wir den Grad der vorherigen Beispiele auf 2 statt auf 3 setzen, werden die Knoten kleiner, und die Anzahl von Kontrollpunkten periodischer Kurven ändert sich.
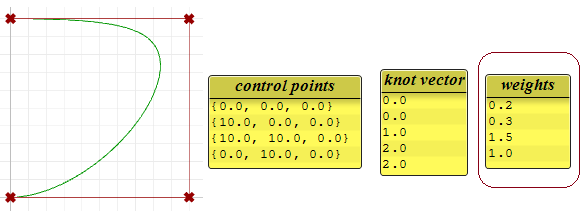
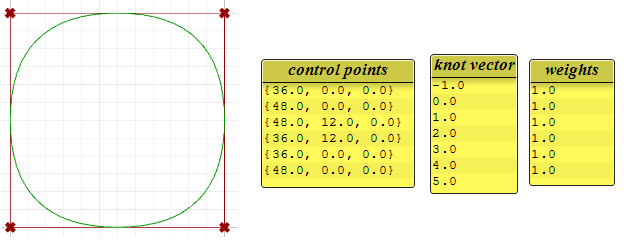
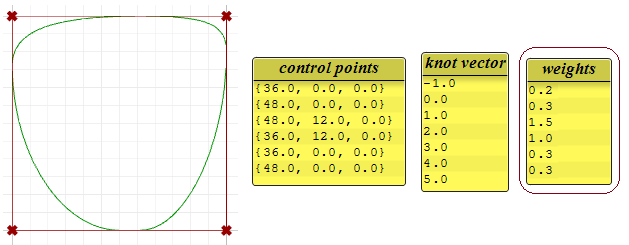
Wichtungen
Wichtungen von Kontrollpunkten in einer gleichförmigen NURBS-Kurve sind auf 1 eingestellt, aber diese Zahl kann in rationalen NURBS-Kurven variieren. Das folgende Beispiel zeigt die Wirkung der Wichtungsveränderung bei Kontrollpunkten.
Auswertung von NURBS-Kurven
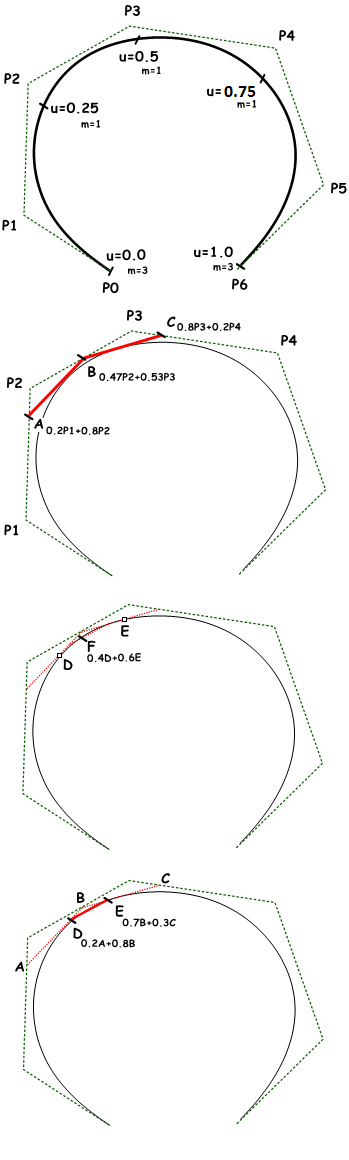
Der nach seinem Erfinder Carl de Boor benannte De-Boor-Algorithmusm ist eine Verallgemeinerung des de Casteljau-Algorithmus für Bézier-Kurven. Er ist numerisch stabil und seine Verwendung zur Auswertung von Punkten auf NURBS-Kurven in 3D-Anwendungen ist weit verbreitet. Das folgende ist ein Beispiel für die Auswertung eines Punkts auf einer NURBS-Kurve dritten Grades unter Verwendung des De-Boor-Algorithmus.
Eingabe:
Sieben Kontrollpunkte
$$P0$$ bis
$$P6$$
Knoten:
$$u_0 = 0.0$$
$$u_1 = 0.0$$
$$u_2 = 0.0$$
$$u_3= 0.25$$
$$u_4 = 0.5$$
$$u_5 = 0.75$$
$$u_6 = 1.0$$
$$u_7 = 1.0$$
$$u_8 = 1.0$$
Ausgabe:
Punkt auf Kurve der auf $$u=0.4$$ liegt
Lösung:
1. .Berechnen Sie die Koeffizienten für die erste Iteration:
$$A_c = ((u – u_1)/(u_{1+3} – u_1) = 0.8$$
$$B_c = (u – u_2)/(u_{2+3} – u_2) = 0.53$$
$$C_c = (u – u_3)/(u_{3+3} – u_3) = 0.2$$
2. Berechnen Sie die Punkte unter Verwendung von Koeffizienten-Daten:
$$A = 0.2P_1 + 0.8P_2$$
$$B = 0.47 P_2 + 0.53 P_3$$
$$C = 0.8 P_3 + 0.2 P_4$$
3. Berechnen Sie die Koeffizienten für die zweite Iteration:
$$D_c = (u – u_2) / (u_{2+3-1} – u_2) = 0.8$$
$$E_c = (u – u_3) / (u_{3+3-1} – u_3) = 0.3$$
4. Berechnen Sie die Punkte unter Verwendung von Koeffizienten-Daten:
$$D = 0.2A+ 0.8B$$
$$E = 0.7B + 0.3C$$
5. Berechnen Sie den letzten Koeffizienten:
$$Fc = (u – u_3)/ (u_{3+3-2} – u_3) = 0.6$$
Suchen Sie den Punkt auf Kurve an $$u=0.4$$-Parameter:
$$F= 0.4D + 0.6E$$
Geometrische Kurvenstetigkeit
Stetigkeit ist ein wichtiges Konzept in der 3D-Modellierung. Stetigkeit ist wichtig, um visuelle Glätte wie auch sanftes Licht und Luftströmung zu erhalten. Die folgende Tabelle enthält verschiedene Stetigkeiten und ihre Definitionen:
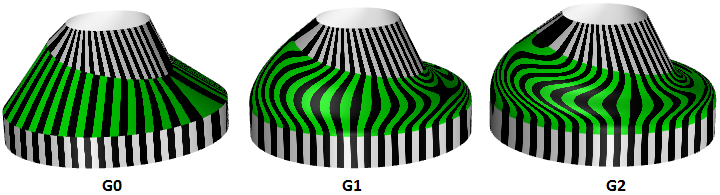
G0| (Positionsstetig) | Zwei miteinander verbundene Kurvensegmente |
| G1| (Tangentenstetig) | Die Richtung der Tangente am Verbindungspunkt ist für beide Kurvensegmente gleich. |
| G2| ( Krümmungsstetig) | Krümmungen wie auch Tangenten stimmen für beide Kurvensegmente am gemeinsamen Endpunkt überein. |
| GN|……. | Die Kurven stimmen übergeordnet miteinander ein |
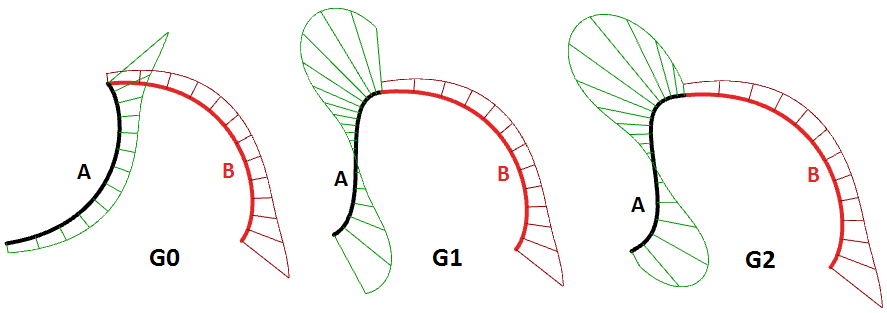
3.4 Kurvenkrümmung
Krümmung ist ein bei der Modellierung von 3D-Kurven und -Flächen viel verwendetes Konzept. Krümmung wird definiert als die Änderung in der Neigung einer Tangente zu einer Kurve über eine Bogeneinheitslänge. Für einen Kreis oder eine Kugel ist dies der Kehrwert des Radius und über die gesamte Domäne hinweg konstant.
An jedem beliebigen Punkt auf einer Kurve in der Ebene ist die tangentiale Linie die Linie, die sich der Kurve durch diesen Punkt am meisten nähert. Wir können auch den besten annähernden Kreis finden, der durch diesen Punkt verläuft und tangential zur Kurve liegt. Der Kehrwert des Radius dieses Kreises ist die Krümmung der Kurve an diesem Punkt.
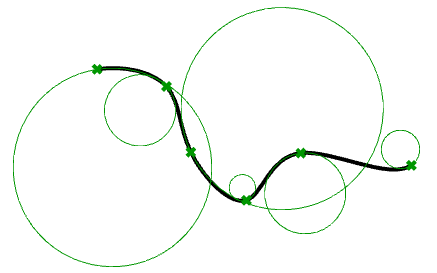
Der beste annähernde Kreis kann sich entweder links oder rechts der Kurve befinden. Wenn wir uns dies bewusst machen, stellen wir eine Konvention her, wie die Erteilung des positiven Krümmungszeichens wenn der Kreis links, und des negativen Zeichens wenn der Kreis rechts der Kurve liegt. Dies wird Krümmung mit Zeichen genannt. Krümmungswerte verbundener Kurven zeigen Stetigkeit zwischen diesen Kurven an.
3.5 Parametrische Flächen
Flächenparameter
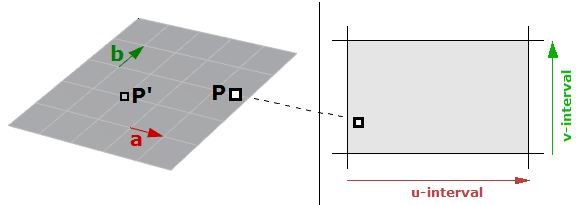
Eine parametrische Fläche ist eine Funktion zweier unabhängiger Parameter (meist $$u$$, $$v$$ genannt) über einer zweidimensionalen Domäne. Nehmen wir zum Beispiel eine Ebene Fläche. Wir haben einen Punkt $$P$$ auf dieser Ebenen Fläche und zwei nicht-parallele Vektoren auf der Ebene, $$\vec a$$ und $$\vec b$$, also können wir eine parametrische Gleichung der Ebenen Fläche hinsichtlich der beiden Parameter $$u$$ und $$v$$ wie folgt definieren:
$$P = P’ + u * \mathbf{\vec a} + v * \mathbf{\vec b}$$Wobei:
$$P’$$: ein bekannter Punkt auf der Ebene ist
$$\mathbf{\vec a}$$: der erste Vektor auf der Ebene ist
$$\mathbf{\vec b}$$: der erste Vektor auf der Ebene ist
$$u$$: der erste Parameter ist
$$v$$: der erste Parameter ist
Ein weiteres Beispiel ist die Kugel. Die Cartesianische Gleichung einer am Ursprung zentrierten Kugel mit Radius $$R$$ ist
$$x^2 + y^2 + z^2 = R^2$$Das bedeutet, dass es für jeden Punkt drei Variablen ( $$x$$, $$y$$, $$z$$) gibt, was für eine parametrische Darstellung, in der nur zwei Variablen nötig sind, nicht sehr nützlich ist. Im kugelförmigen Koordinatensystem jedoch verwendet jeder Punkt die drei Werte:
$$r$$: Radialabstand zwischen Punkt und Ursprung
$$θ$$: der Winkel von der x-Achse in der xy-Ebene
$$ø$$: der Winkel von z-Achse und Punkt
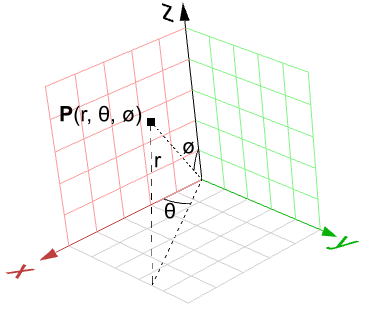
Eine Punktumwandlung von kugelförmiger zu Cartesianischer Koordinate erhält man wie folgt:
$$x = r * sin(ø) * cos(θ)$$
$$y = r * sin(ø) * sin(θ)$$
$$z = r * cos (ø)$$
Wobei:
$$r$$ Entfernung vom Ursprung
$$≥ 0$$ ist
$$θ$$ von
$$0$$ bis
$$2π$$ läuft
$$ø$$ von
$$0$$ bis
$$π$$ läuft
Da $$r$$ in einer kugelförmigen Oberfläche konstant ist, verbleiben uns nur zwei Variablen, daher können wir die obige zur Erstellung einer parametrischen Darstellung einer kugelförmigen Fläche verwenden:
$$u = θ$$
$$v = ø$$
So dass:
$$x = r * sin(v) * cos(u)$$
$$y = r * sin(v) * sin(u)$$
$$z = r * cos(v)$$
Wobei ( $$u$$, $$v$$) innerhalb des Bereichs ( $$2 π$$, $$π$$) liegt
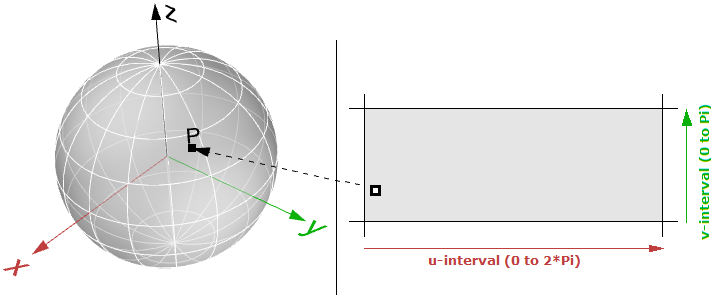
Die parametrische Fläche folgt der Form:
$$x = x(u,v)$$
$$y = y(u,v)$$
$$z = z(u,v)$$
Wobei:
$$u$$ und $$v$$ die beiden Parameter innerhalb der Flächendomäne oder -region sind.
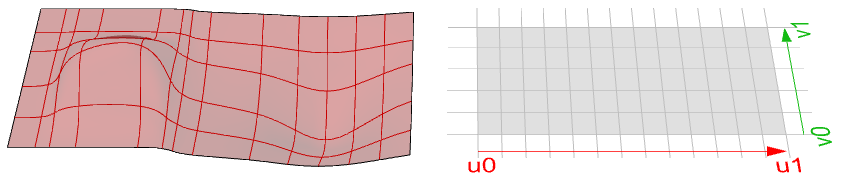
Flächendomäne
Eine Flächendomäne wird definiert als der Bereich von ( $$u,v$$)-Parametern, die zu 3D-Punkten auf dieser Fläche ausgewertet werden. Die Domäne in jeder Dimension ( $$u$$ oder $$v$$) wird gewöhnlich als zwei reelle Zahlen beschrieben ( $$u_{min}$$ bis $$u_{max}$$) und ( $$$v_{min}$$ bis $$$v_{max}$$)
Die Änderung einer Flächendomäne wird als Reparametrisierung der Fläche beschrieben. Eine ansteigende Domäne bedeutet, dass der Minimalwert der Domäne zum Minimalpunkt der Fläche weist. Üblicherweise, jedoch nicht immer, sind Domänen ansteigend.
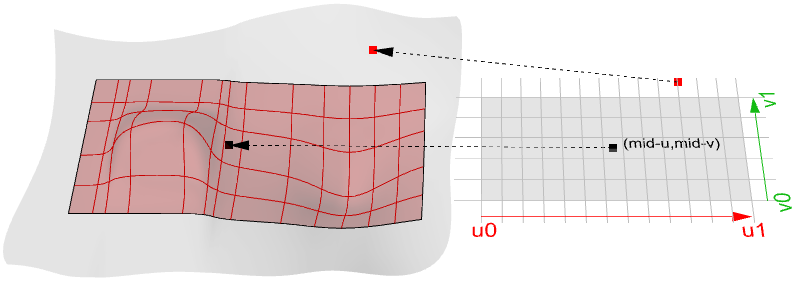
Flächenauswertung
Die Auswertung einer Fläche auf einem Parameter innerhalb der Flächendomäne ergibt einen Punkt auf der Fläche. Bedenken Sie, dass die Mitte der Domäne ( $$u_{mid}$$, $$v_{mid}$$) nicht unbedingt zum Mittelpunkt der 3D-Fläche ausgewertet wird. Auch wird die Auswertung der $$u-$$ und $$v-$$-Werte, die sich außerhalb der Flächendomäne befinden, kein gutes Ergebnis erbringen.
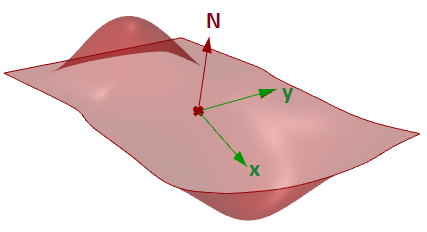
Tangentiale Ebene einer Fläche
Die zu einer Fläche an einem gegebenen Punkt tangentiale Ebene ist die Ebene, die die Fläche an diesem Punkt berührt. Die z-Richtung der tangentialen Ebene repräsentiert die Normalenrichtung der Fläche an diesem Punkt.
3.6 Geometrische Flächenstetigkeit
Viele Modelle können nicht anhand einer einzigen Füllfläche erzeugt werden. Stetigkeit zwischen verbundenen Füllflächen ist von Bedeutung für visuelle Glätte, Lichtreflektierung und Luftströmung. Die folgende Tabelle enthält verschiedene Stetigkeiten und ihre Definitionen:
G0| (Positionsstetig) | Zwei miteinander verbundene Flächen. |
| G1| (Tangentenstetig) | Die einander entsprechenden Tangenten der beiden Flächen entlang ihrer Verbindungskante sind sowohl in u- als auch v-Richtung parallel. |
| G2| ( Krümmungsstetig) | Krümmungen wie auch Tangenten stimmen für beide Flächen an der gemeinsamen Kante überein. |
| GN|……. Die Flächen stimmen übergeordnet miteinander ein. |
3.7 Flächenkrümmung
Für Flächen ist die Normalenkrümmung eine Verallgemeinerung der Krümmung an Flächen. Angenommen, wir haben einen Punkt auf der Fläche und eine in der tangentialen Ebene der Fläche auf diesem Punkt liegende Richtung, dann wird die Krümmung von Normalen-Schnittkurven durch Überschneidung der Fläche mit der durch den Punkt gespannten Ebene, der Normalen zur Fläche an diesem Punkt und der Richtung berechnet. Die Krümmung von Normalen-Schnittkurven ist die Krümmung mit Zeichen dieser Kurve am relevanten Punkt.
Wenn wir alle Richtungen in der zur Fläche tangentialen Ebene an unserem Punkt betrachten und die Normalenkrümmung in all diesen Richtungen berechnen, wird es einen maximalen und einen minimalen Wert geben.
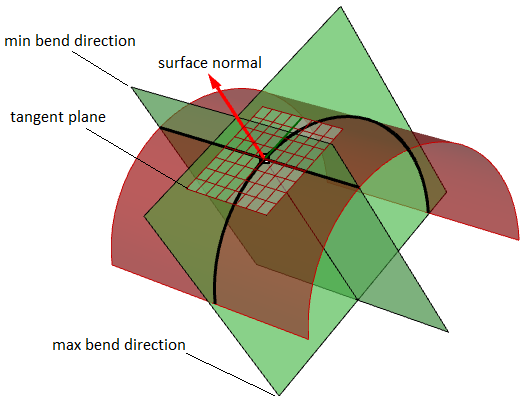
Hauptkrümmungen
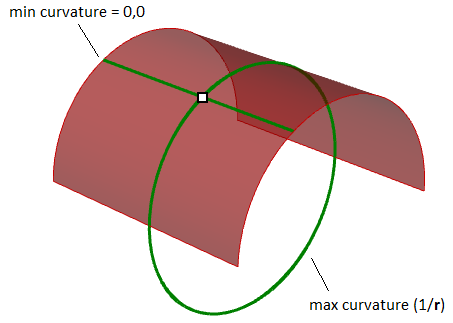
Die Hauptkrümmungen einer Fläche an einem Punkt sind die minimalen und maximalen Werte der Normalen-Krümmungen an diesem Punkt. Sie messen die maximale und minimale Biegung der Fläche an diesem Punkt. Hauptkrümmungen werden verwendet, um Gaußsche und mittlere Krümmungen der Fläche zu berechnen.
In einer zylindrischen Fläche zum Beispiel besteht keine Biegung entlang der linearen Richtung (Krümmung ist gleich Null), wogegen die maximale Biegung beim Überschneiden mit einer zu den Endseiten parallelen Ebene besteht (Krümmung ist gleich 1/Radius). Diese beiden Extremen machen die Hauptkrümmungen auf dieser Fläche.
Gaußsche Krümmung
Die Gaußsche Krümmung einer Fläche an einem Punkt ist das Produkt der Hauptkrümmungen an diesem Punkt. Die tangentiale Ebene jeglichen Punkts mit positiver Gaußscher Krümmung berührt die Fläche lokal an einem einzigen Punkt, während die tangentiale Ebene jeglichen Punkts mit negativer Gaußscher Krümmung die Fläche schneidet.
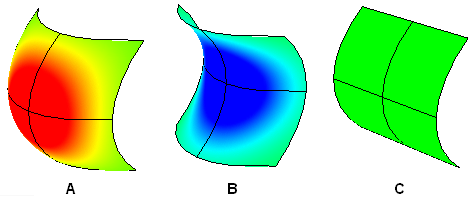
A: Positive Krümmung wenn die Fläche schüsselähnlich ist.
B: Negative Krümmung wenn die Fläche sattelähnlich ist.
C: Krümmung von null wenn die Fläche in mindestens einer Richtung flach ist (Ebene, Zylinder).
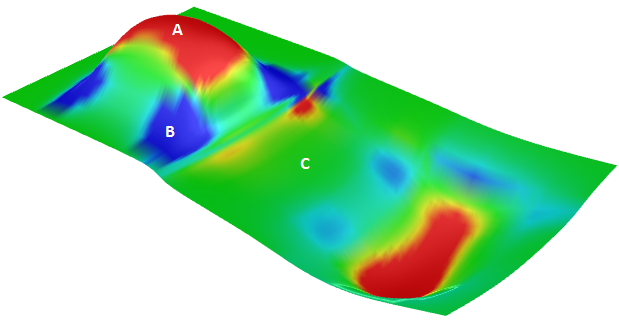
Mittlere Krümmung
Die mittlere Krümmung einer Fläche an einem Punkt ist halb so groß wie die Summen der Hauptkrümmungen an diesem Punkt. Alle Punkte mit einer mittleren Krümmung von null haben eine negative Gaußsche Krümmung oder eine von null.
Flächen mit einer mittleren Krümmung von null in allen Punkten sind Minimalflächen. Mittels Minimalflächen modellierbare physikalische Prozesse schließen die Erzeugung auf feste Objekte (z. B. Drahtschleifen) gespannter Seifenfilme mit ein. Ein Seifenfilm wird nicht durch den Luftdruck (der auf beiden Seiten gleich ist) verzerrt und kann seine Fläche frei minimieren. Das steht im Gegensatz zur Seifenblase, die eine bestimmte Luftmenge einschließt und deren Druck innen und außen nicht gleich ist. Mittlere Krümmung ist hilfreich, um Flächen mit abrupter Änderung in der Flächenkrümmung zu finden.
Flächen mit konstanter mittlerer Krümmung werden oft CMC-Flächen (CMC: Constant Mean Curvature) genannt. CMC-Flächen schließen auch die Erzeugung von Seifenblasen mit ein, sowohl frei als auch an Objekte angehängt. Im Gegensatz zu einem einfachen Seifenfilm umschließt eine Seifenblase ein Volumen und existiert in einem Gleichgewicht, bei dem der etwas höhere Druck im Inneren der Blase durch die flächenverkleinernden Kräfte der Blase selbst ausgeglichen wird.
3.8 NURBS-Flächen
Sie können sich NURBS-Flächen als ein Raster von NURBS-Kurven vorstellen, die in zwei Richtungen verlaufen. Die Form einer NURBS-Fläche wird durch eine Zahl von Kontrollpunkten bestimmt, sowie den Grad dieser Fläche in jede dieser beiden Richtungen (u- und v-Richtungen). NURBS-Flächen sind effizient bei der Speicherung und Darstellung von Freiformflächen mit hohem Genauigkeitsgrad. Die mathematischen Gleichungen und Details von NURBS-Flächen gehen über den Rahmen dieses Texts hinaus. Stattdessen konzentrieren wir uns lieber auf die für Designer relevantesten Eigenschaften.
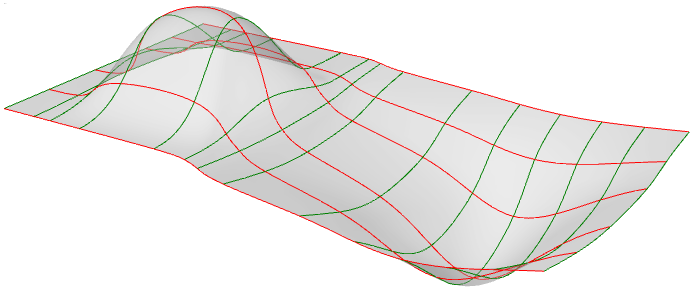
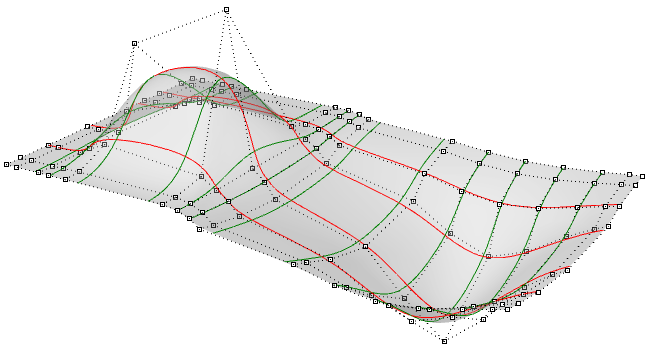
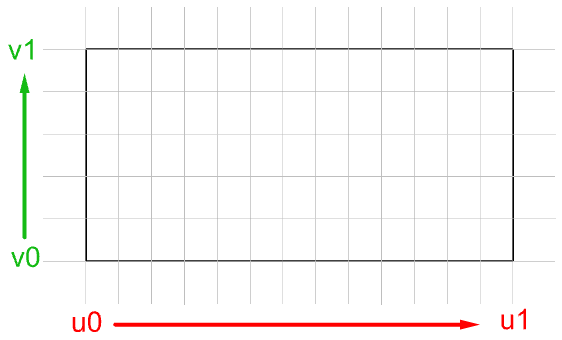
Die Auswertung von Parametern in gleichen Intervallen im 2D-Parameterrechteck ergibt meistens keine gleichen Intervalle im 3D-Raum.
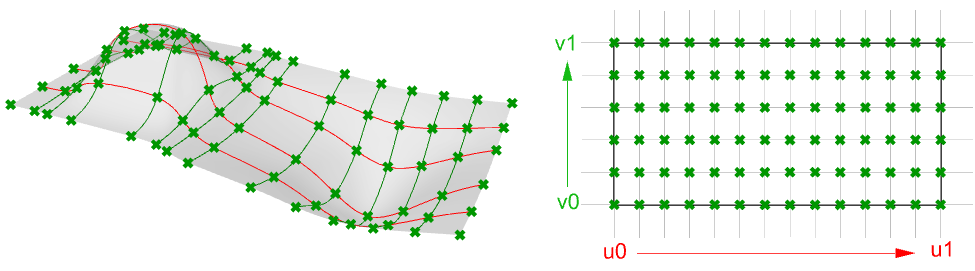
Eigenschaften von NURBS-Flächen
Die Eigenschaften von NURBS-Flächen sind denen von NURBS-Kurven sehr ähnlich, nur dass es noch einen zusätzlichen Parameter gibt. NURBS-Flächen enthalten die folgenden Informationen:
- Bemaßung, üblicherweise 3
- Grad in u und v-Richtungen: (manchmal wird Ordnung verwendet, also Grad + 1)
- Kontrollpunkte (Punkte)
- Wichtungen von Kontrollpunkten (Zahlen)
- Knoten (Zahlen)
Wie schon bei den NURBS-Kurven brauchen Sie wahrscheinlich nicht im Einzelnen zu wissen, wie eine NURBS-Fläche erzeugt wird, da 3D-Modellierer hierfür üblicherweise gute Werkzeuge bereitstellen. Flächen (wie auch Kurven) können Sie stets zu einem neuen Grad und mit einer neuen Zahl von Kontrollpunkten wiederaufbauen. Eine Fläche kann offen, geschlossen oder periodisch sein. Hier sind einige Beispiele für Flächen:
| Fläche ersten Grades sowohl in u- als auch v-Richtungen. Alle Kontrollpunkte liegen auf der Fläche. | 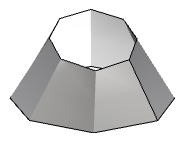 |
| Offene Fläche dritten Grades in der u-Richtung und ersten Grades in der v-Richtung. Die Eckpunkte der Fläche stimmen mit den Eckpunkt-Kontrollpunkten überein. | 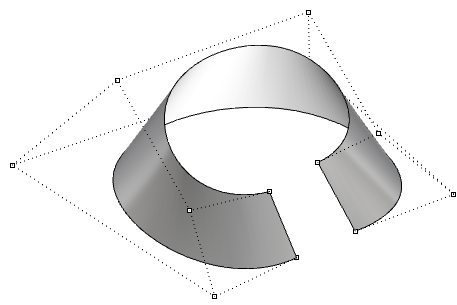 |
| Geschlossene (nicht-periodische) Fläche dritten Grades in der u-Richtung und ersten Grades in der v-Richtung. Einige Kontrollpunkte stimmen mit der Flächennaht überein. | 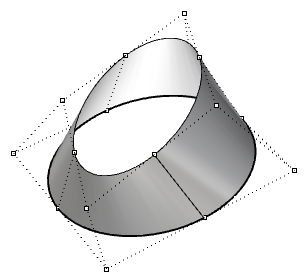 |
| Das Verschieben von Kontrollpunkten einer geschlossenen (nicht-periodischen) Fläche verursacht einen Knick und die Fläche sieht nicht glatt aus. | 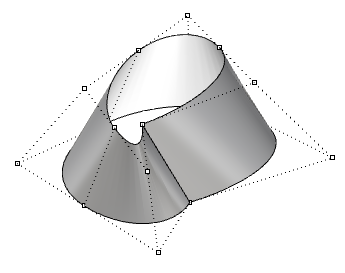 |
| Periodische Fläche dritten Grades in der u-Richtung und ersten Grades in der v-Richtung. Die Flächenkontrollpunkte stimmen nicht mit der Flächennaht überein. | 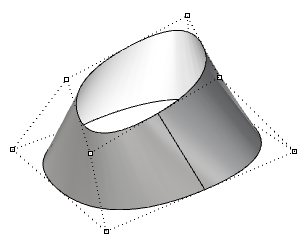 |
| Das Verschieben von Kontrollpunkten einer periodischen Fläche wirkt sich nicht auf die Glätte der Fläche aus und führt nicht zu Knicken. | 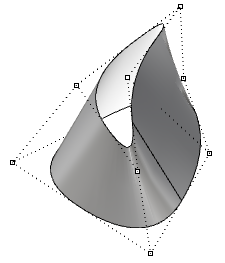 |
Singularität in NURBS-Flächen
Wenn Sie zum Beispiel eine lineare Kante einer einfachen Ebene haben und die beiden Endkontrollpunkte einer Kante so ziehen, dass sie an der Mitte überlappen (zusammenfallen), erhalten Sie eine singuläre Kante. Sie werden bemerken, dass die Flächen-Isokurven an dem singulären Punkt zusammenlaufen.
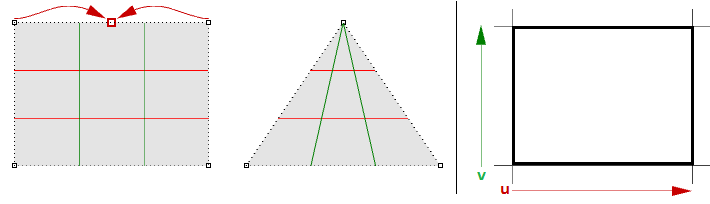
Die dreieckige Form oben kann ohne Singularität erzeugt werden. Sie können eine Fläche mit einer dreieckigen Polylinie trimmen. Bei Überprüfung der darunterliegenden NURBS-Struktur sehen Sie, dass sie als eine rechteckige Form verbleibt.
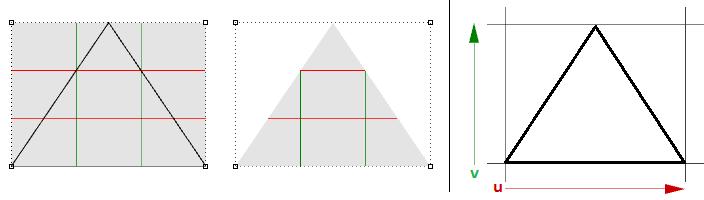
Weitere häufige Beispiele für Flächen, die ohne Singularität schwer zu erzeugen sind, sind Kegel und Kugel. Die Spitze eines Kegels und die oberen und unteren Kanten einer Kugel fallen alle zu einem Punkt zusammen. Ob eine Singularität besteht oder auch nicht, das Parameterrechteck behält eine mehr oder weniger rechteckige Region bei.
Getrimmte NURBS-Flächen
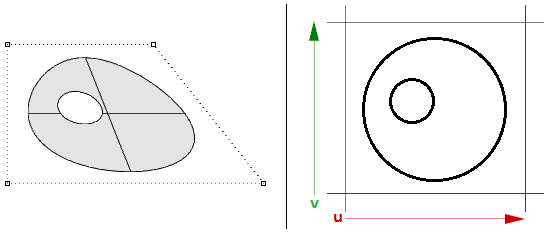
NURBS-Flächen können getrimmt oder ungetrimmt sein. Getrimmte Flächen verwenden eine darunterliegende NURBS-Fläche und geschlossene Kurven, um einen Teil dieser Fläche herauszutrimmen. Jede Fläche hat eine geschlossene Kurve, welche die äußere Kante (äußere Schleife) bestimmt, und sie kann nicht-überschneidende, geschlossene innere Kurven zur Bestimmung von Öffnungen (innere Schleifen) haben. Eine Fläche mit einer äußeren Schleife, welche die gleiche wie die ihrer darunterliegenden NURBS-Fläche ist und keine Öffnungen hat, ist was wir eine ungetrimmte Fläche nennen.
3.9 Flächenverbände
Ein Flächenverband besteht aus zwei oder mehr (möglicherweise getrimmten) miteinander verbundenen NURBS-Flächen. Jede Fläche hat ihre eigene Struktur, Parametrisierung und Isokurven-Richtungen, die nicht übereinstimmen müssen. Flächenverbände werden unter Verwendung des Begrenzungsflächenmodells (BRep*) dargestellt. Die BRep-Struktur beschreibt Flächen, Kanten und Scheitelpunkte mit Trimmdaten und Verbindung unterschiedlicher Teile. Getrimmte Flächen werden auch unter Verwendung von BRep-Datenstruktur dargestellt.

Das BRep ist eine Datenstruktur, die jede Seite hinsichtlich ihrer darunterliegenden Fläche, umlaufenden 3D-Kanten, Scheitelpunkte, 2D-Trimmungen des Parameterraums und der Beziehung aneinander grenzender Seiten beschreibt. BRep-Objekte werden auch Volumenkörper genannt, wenn sie geschlossen (wasserdicht) sind.
Ein Beispiel-Flächenverband ist ein einfacher Quader, der aus sechs miteinander verbundenen, ungetrimmten Flächen besteht.
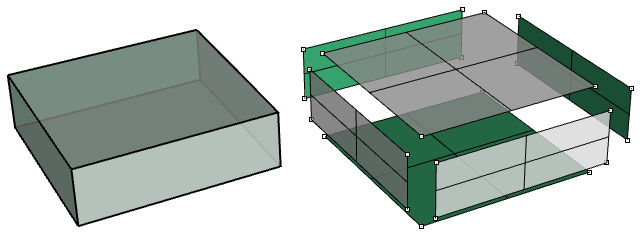
Derselbe Quader kann auch aus getrimmten Flächen erzeugt werden, wie der obere im folgenden Beispiel.
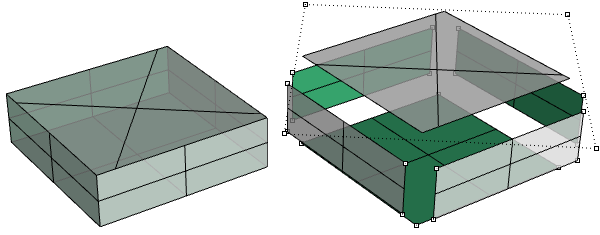
Die oberen und unteres Seiten des Zylinders im folgenden Beispiel sind aus planaren Flächen getrimmt.
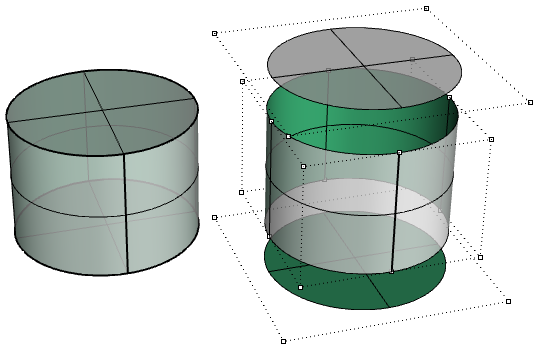
Wie wir sehen konnten, ist die Bearbeitung von NURBS-Kurven und ungetrimmten Flächen intuitiv und kann interaktiv durch Verschieben von Kontrollpunkten geschehen. Die Bearbeitung getrimmter Flächen und Flächenverbände kann jedoch eine Herausforderung darstellen. Am schwierigsten ist es dabei, die verbundenen Kanten verschiedener Seiten innerhalb der gewünschten Toleranz zu halten. Benachbarte Seiten mit gemeinsamen Kanten können getrimmt werden und haben üblicherweise keine übereinstimmende NURBS-Struktur, weswegen die Deformierung der Kante aufgrund einer Änderung des Objekts zu einer Lücke führen kann.
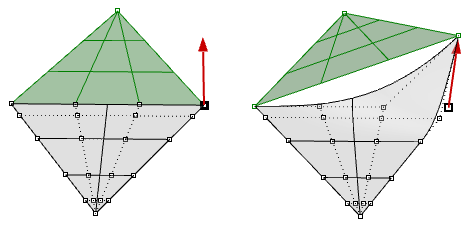
Schwierigkeiten bereitet auch die meist geringere Kontrolle über das Ergebnis, besonders beim Verändern getrimmter Geometrie.
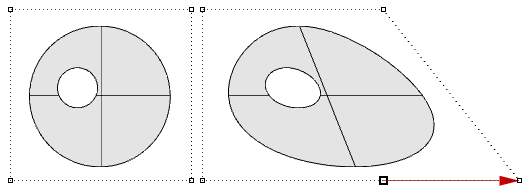
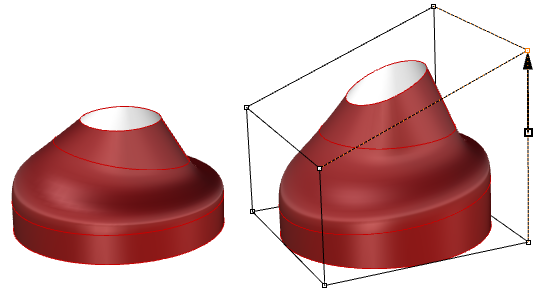
Getrimmte Flächen werden im Parameterraum unter Verwendung der darunterliegenden ungetrimmten Fläche beschrieben, in Kombination mit den 2D-Trimmkurven, die innerhalb der 3D-Fläche zu den 3D-Kanten ausgewertet werden.
3.10 Tutorials
Die folgenden Tutorials verwenden die in diesem Kapitel erlernten Konzepte. Die Software ist Rhinoceros 5 und Grasshopper 0.9.
3.10.1 Stetigkeit zwischen Kurven
Überprüfen Sie die Stetigkeit zwischen zwei Eingabekurven. Stetigkeit setzt voraus, dass die Kurven am Ende der ersten Kurve und am Beginn der zweiten Kurve aufeinandertreffen.
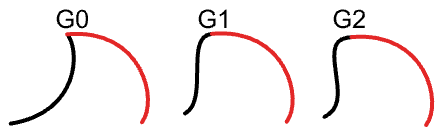
Eingabe:
Zwei Eingabekurven.
Parameter:
Führen Sie folgende Berechnung durch, um die Stetigkeit zwischen zwei Kurven bestimmen zu können:
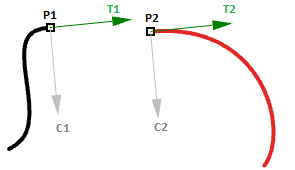
- Endpunkt der ersten Kurve ( $$P1$$)
- Startpunkt der zweiten Kurve ( $$P2$$)
- Tangente am Ende der ersten Kurve und am Beginn der zweiten Kurve ( $$T1$$ und $$T2$$).
- Krümmung am Ende der ersten Kurve und am Beginn der zweiten Kurve ( $$C1$$ und $$C2$$).
Lösung:
1. Reparametrisieren Sie die Eingabekurven. Ziel ist zu wissen, dass der Beginn der Kurve auf
$$t=0$$ und das Ende auf
$$t=1$$ ausgewertet wird.
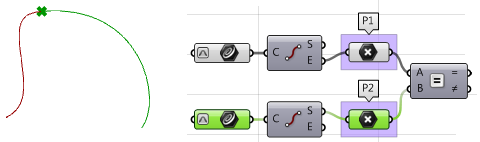
2. Extrahieren Sie die End- und Startpunkte der beiden Kurven und überprüfen Sie, ob Sie übereinstimmen. Ist dies der Fall, sind die beiden Kurven zumindest
$$G0$$-stetig.
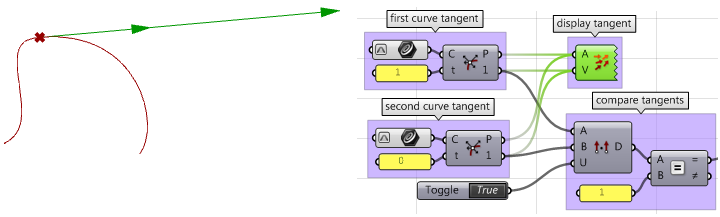
3. Berechnen Sie die Tangenten.
4. .Vergleichen Sie die Tangenten unter Verwendung des Punktprodukts. Vergewissern Sie sich, dabei Vektoren zu verwenden. Wenn die Kurven parallel sind, haben wir mindestens
$$G1$$-Stetigkeit.
5. Berechnen Sie die Krümmungsvektoren.
6. Vergleichen Sie die Krümmungsvektoren, und wenn sie übereinstimmen, sind beide Kurven
$$G2$$-stetig.
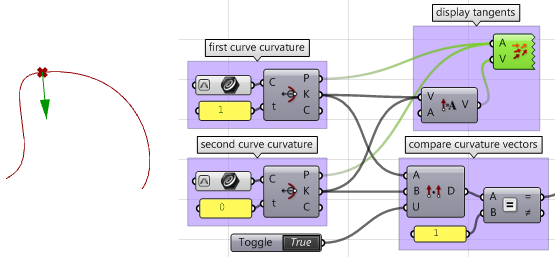
7. Erzeugen Sie Logik zum Durchfiltern der drei Ergebnisse (G1, G2 und G3) und wählen Sie die höchste Stetigkeit.
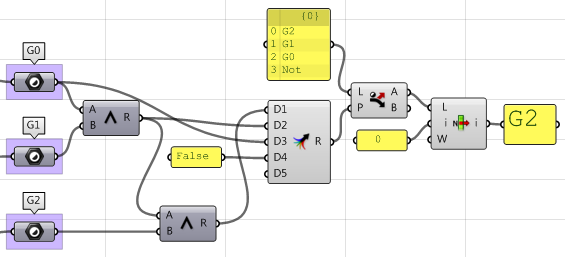
Unter Verwendung der Grasshopper-VBScript-Komponente:
Private Sub RunScript(ByVal c1 As Curve, ByVal c2 As Curve, ByRef A As Object)
'declare variables
Dim continuity As New String("")
Dim t1, t2 As Double
Dim v_c1, v_c2, c_c1, c_c2 As Vector3d
'extract start and end points
Dim end_c1 = c1.PointAtEnd
Dim start_c2 = c2.PointAtStart
'check G0 continuity
If end_c1.DistanceTo(start_c2) = 0 Then
continuity = "G0"
End If
'check G1 continuity
If continuity = "G0" Then
'calculate tangents
v_c1 = c1.TangentAtEnd
v_c2 = c2.TangentAtStart
'unitize tangent vectors
v_c1.Unitize
v_c2.Unitize
'compare tangents
If v_c1 * v_c2 = 1.0 Then
continuity = "G1"
End If
End If
'check G2 continuity
If continuity = "G1" Then
'extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max
t2 = c2.Domain.Min
'calculate curvature
c_c1 = c1.CurvatureAt(t1)
c_c2 = c2.CurvatureAt(t2)
'unitize curvature vectors
c_c1.Unitize
c_c2.Unitize
'compare vectors
If c_c1 * c_c2 = 1.0 Then
continuity = "G2"
End If
End If
'Assign output
A = continuity
End Sub
Unter Verwendung der Grasshopper-Python-Komponente:
#decclare variables
continuity = ""
#extract start and end points
end_c1 = c1.PointAtEnd
start_c2 = c2.PointAtStart
#check G0 continuity
if end_c1.DistanceTo(start_c2) == 0:
continuity = "G0"
#check G1 continuity
if continuity == "G0":
#calculate tangents
v_c1 = c1.TangentAtEnd
v_c2 = c2.TangentAtStart
#unitize tangent vectors
v_c1.Unitize()
v_c2.Unitize()
#compare tangents
dot = v_c1 * v_c2
if dot == 1.0:
continuity = "G1"
else:
print("Failed G1")
print(dot)
#check G2 continuity
if continuity == "G1":
#extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max
t2 = c2.Domain.Min
#calculate curvature
c_c1 = c1.CurvatureAt(t1)
c_c2 = c2.CurvatureAt(t2)
#unitize curvature vectors
c_c1.Unitize()
c_c2.Unitize()
#compare vectors
dot = c_c1 * c_c2
if dot == 1.0:
continuity = "G2"
else:
print("Failed G2")
print(dot)
#assign output
A = continuity
Unter Verwendung der Grasshopper-C#-Komponente:
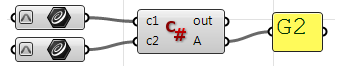
Private Sub RunScript(ByVal c1 As Curve, ByVal c2 As Curve, ByRef A As Object)
//decalre variables
string continuity = ("");
double t1, t2;
Vector3d v_c1, v_c2, c_c1, c_c2;
//extract start and end points
Point3d end_c1 = c1.PointAtEnd;
Point3d start_c2 = c2.PointAtStart;
//check G0 continuity
if( end_c1.DistanceTo(start_c2) == 0){
continuity = "G0";
}
//check G1 continuity
if( continuity == "G0")
{
//calculate tangents
v_c1 = c1.TangentAtEnd;
v_c2 = c2.TangentAtStart;
//unitize tangent vectors
v_c1.Unitize();
v_c2.Unitize();
//compare tangents
if( v_c1 * v_c2 == 1.0 ){
continuity = "G1";
}
}
//check G2 continuity
if( continuity == "G1" )
{
//extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max;
t2 = c2.Domain.Min;
//calculate curvature
c_c1 = c1.CurvatureAt(t1);
c_c2 = c2.CurvatureAt(t2);
//unitize curvature vectors
c_c1.Unitize();
c_c2.Unitize();
//compare vectors
if( c_c1 * c_c2 == 1.0 ){
continuity = "G2";
}
}
//assign output
A = continuity;
End Sub
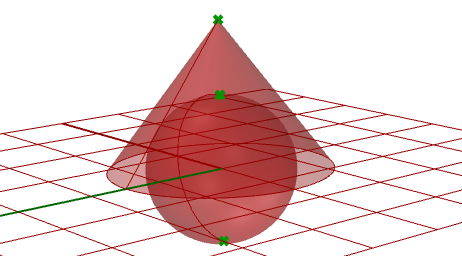
3.10.2 Flächen mit Singularität
Extrahieren Sie singuläre Punkte in einer Kugel und einem Kegel.
Eingabe:
Eine Kugel und ein Kegel.
Parameter:
Singularität kann durch Analysieren der 2D-Parameterraumtrimmungen gefunden werden, deren entsprechende Kanten ungültig sind oder die Länge Null aufweisen. Diese Trimmungen sollten singulär sein.
Lösung:
- Durchqueren Sie alle Trimmungen in der Eingabe.
- Überprüfen Sie ob eine der Trimmungen eine ungültige Kante aufweist und vermerken Sie sie als singuläre Trimmung.
- Extrahieren Sie Punktpositionen im 3D-Raum.
Unter Verwendung der Grasshopper-VB-Komponente:
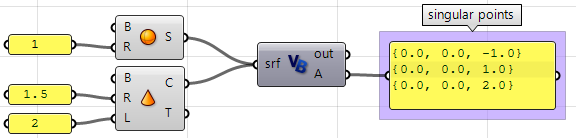
Private Sub RunScript(ByVal srf As Brep, ByRef A As Object)
'Decalre a new list of points
Dim singular_points As New List( Of Point3d)
'Examine all trims in the input
For Each trim As BrepTrim In srf.Trims
'Null edge of a trim indicates a singularity
If trim.Edge Is Nothing Then
'Find the 2D parameter space point of the start or end of the trim
Dim pt2d = New Point2d(trim.PointAtStart)
'Evaluate trim end point on the object surface
Dim pt3d = trim.Face.PointAt(pt2d.x, pt2d.y)
'Add 3D point to the list of singular points
singular_points.Add(pt3d)
End If
Next
'Asign output
A = singular_points
End Sub
Unter Verwendung der Grasshopper-Python-Komponente:
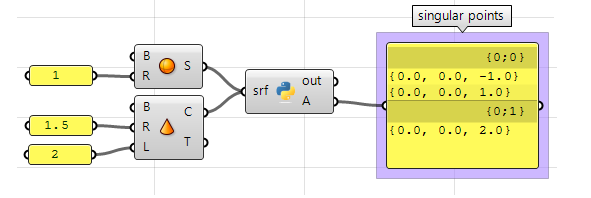
#Declare a new list of points
singular_points = []
#Examine all trims in the input brep
for trim in srf.Trims:
#Null edge of a trim indicates a singularity
if trim.Edge == None:
#Find the 2D parameter space point at trim start or end
pt2d = trim.PointAtStart
#Evaluate trim end point on the object surface
pt3d = trim.Face.PointAt(pt2d.X, pt2d.Y)
#Add 3D point to the list of singular points
singular_points.append(pt3d)
#Asign output
A = singular_points
Unter Verwendung der Grasshopper-C#-Komponente:
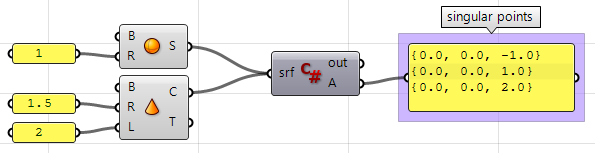
private void RunScript(Brep srf, ref object A)
{
//Decalre a new list of points
List < Point3d > singular_points = new List<Point3d>();
//Examine all trims in the input
foreach( BrepTrim trim in srf.Trims)
{
//Null edge of a trim indicates a singularity
if( trim.Edge == null)
{
//Find the 2D parameter space point of the start or end of the trim
Point2d pt2d = new Point2d(trim.PointAtStart);
//Evaluate trim end point on the object surface
Point3d pt3d = trim.Face.PointAt(pt2d.X, pt2d.Y);
//Add 3D point to the list of singular points
singular_points.Add(pt3d);
}
}
//Asign output
A = singular_points
}
Beispieldateien herunterladen
Laden Sie das Archiv download samplesand tutorials herunter, das alle Grasshopper-Beispiele und Codedateien in diesem Leitfaden enthält.
Weitere Schritte:
Für weiterführende Informationen lesen Sie den Leitfaden Referenzen, um mehr über die detaillierte Struktur von NURBS-Kurven und -Flächen zu erfahren.

