Ein Vektor zeigt eine Menge an, etwa Geschwindigkeit oder Kraft, welche eine Richtung und Länge aufweist. Vektoren in 3D-Koordinatensystemen werden mit einem geordneten Satz drei reeller Zahlen dargestellt und sehen so aus:
$$\mathbf{\vec v} = <a_1, a_2, a_3>$$1.1 Vektor-Darstellung
In diesem Dokument werden fettgedruckte Kleinbuchstaben mit einem Pfeil darüber zur Bezeichnung von Vektoren verwendet. Vektorenkomponenten werden auch in eckige Klammern gesetzt. Großbuchstaben bezeichnen Punkte. Punktkoordinaten erscheinen immer in Klammern.
Bei Verwendung eines Koordinatensystems und eines beliebigen Ankerpunktsatzes in diesem System können diese Vektoren mittels Liniensegmenten dargestellt oder sichtbar gemacht werden. Eine Pfeilspitze zeigt die Richtung des Vektors an.
Wenn wir zum Beispiel einen Vektor mit einer Richtung parallel zur x–Achse eines bestimmten 3D-Koordinatensystems und einer Länge von 5 Einheiten haben, können wir den Vektor wie folgt schreiben:
$$\mathbf{\vec v} = <5, 0, 0>$$Zur Darstellung dieses Vektors benötigen wir einen Ankerpunkt im Koordinatensystem. Zum Beispiel sind alle Pfeile in der folgenden Abbildung gleichwertige Darstellungen desselben Vektors, ungeachtet der Tatsache, dass sie an unterschiedlichen Standorten verankert sind.
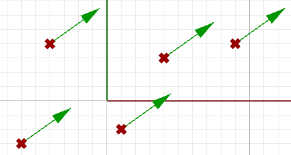
Wie definieren wir also die Endpunkte eines Liniensegments, das einen gegebenen Vektor repräsentiert? Definieren wir zunächst einen Ankerpunkt (A) sodass:
$$A = (1, 2, 3)$$Und einen Vektor:
$$\mathbf{\vec v} = <5, 6, 7>$$Der Endpunkt $$(B)$$ des Vektors wird durch Hinzufügen der entsprechenden Komponenten von Ankerpunkt und Vektor $$\vec v$$ berechnet:
$$B = A + \mathbf{\vec v}$$
$$B = (1+5, 2+6, 3+7) $$
$$B = (6, 8, 10)$$
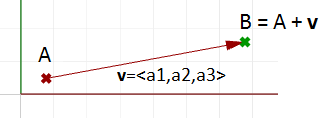
Positionsvektor
Eine spezielle Vektordarstellung verwendet den $$\text{Ursprungspunkt} (0,0,0)$$ als Vektorankerpunkt. Der Standortvektor v= <a_1,a_2,a_3> wird mit einem Liniensegment zwischen zwei Punkten, nämlich Ursprung und B dargestellt, womit:
$$\text{Origin point} = (0,0,0)$$
$$B = (a_1,a_2,a_3)$$
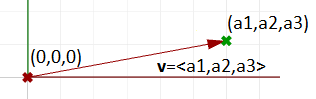
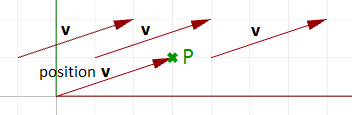
Vektoren im Vergleich zu Punkten
Vektoren und Punkte dürfen nicht verwechselt werden. Es handelt sich dabei um sehr verschiedene Konzepte. Wie bereits erwähnt, stellen Vektoren eine Menge mit einer Richtung und Länge dar, während Punkte einen Standort anzeigen. Norden als Richtung ist zum Beispiel ein Vektor, während der Nordpol ein Standort (Punkt) ist. Angenommen, wir haben einen Vektor und einen Punkt mit den gleichen Komponenten, etwa:
$$\mathbf{\vec v} = <3,1,0>$$
$$P = (3,1,0)$$
Dann können wir Vektor und Punkt folgendermaßen zeichnen:
Vektorlänge
Wie schon erwähnt, haben Vektoren Länge. Wir verwenden $$\vert a \vert$$ um die Länge eines gegebenen Vektors $$ a $$ zu bezeichnen. Zum Beispiel:
$$\mathbf{\vec a} = <4, 3, 0>$$
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5$$
Die Länge eines Vektors $$\mathbf{\vec a} <a_1,a_2,a_3>$$ wird im Allgemeinen wie folgt berechnet:
$$\vert \mathbf{\vec a} \vert = \sqrt{(a_1)^2 + (a_2)^2 + (a_3)^2} $$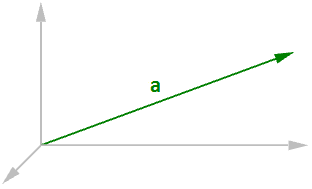
Einheitsvektor
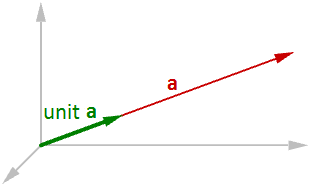
Ein Einheitsvektor ist ein Vektor, dessen Länge einer Einheit entspricht. Einheitsvektoren werden gewöhnlich dazu verwendet, die Richtungen von Vektoren zu vergleichen.
Um einen Einheitsvektor zu berechnen, müssen wir die Länge eines gegebenen Vektors herausfinden und dann die Vektorkomponenten durch die Länge teilen. Zum Beispiel:
$$\mathbf{\vec a} = <4, 3, 0>$$
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5 \text{ Einheitslänge}$$
Wenn
$$\mathbf{\vec b} = \text{Einheitsvektor}$$ von
$$a$$, dann:
$$\mathbf{\vec b} = <4/5, 3/5, 0/5>$$
$$\mathbf{\vec b} = <0.8, 0.6, 0>$$
$$\vert \mathbf{\vec b} \vert = \sqrt{0.8^2 + 0.6^2 + 0^2}$$
$$\vert \mathbf{\vec b} \vert = \sqrt{0.64 + 0.36 + 0}$$
$$\vert \mathbf{\vec b} \vert = \sqrt{(1)} = 1 \text{ Einheitslänge}$$
Generell:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$Der Einheitsvektor von $$\mathbf{\vec a} = <a_1/\vert \mathbf{\vec a} \vert , a_2/\vert \mathbf{\vec a} \vert , a_3/\vert \mathbf{\vec a} \vert >$$
1.2 Vektoroperationen
Skalare Vektoroperation
Skalare Vektoroperation beinhaltet das Multiplizieren eines Vektors mit einer Zahl. Zum Beispiel:
$$\mathbf{\vec a} = <4, 3, 0>$$
$$2* \mathbf{\vec a} = <24, 23, 2*0> $$
$$2*\mathbf{\vec a} = <8, 6, 0>$$
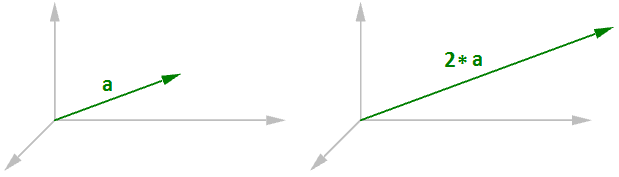
Im Allgemeinen, ein gegebener Vektor $$\mathbf{\vec a} = <a_1, a_2, a_3>$$, und eine reelle Zahl $$t$$
$$t*\mathbf{\vec a} = < t* a_1, t* a_2, t* a_3 >$$Vektoraddition
Für die Vektoraddition sind zwei Vektoren nötig, und das Ergebnis ist ein dritter Vektor. Vektoren addieren wir, indem wir ihre Komponenten addieren.
Wenn wir zum Beispiel zwei Vektoren haben:
$$\mathbf{\vec a} = <1, 2, 0> $$
$$\mathbf{\vec b} = <4, 1, 3> $$
$$\mathbf{\vec a}+\mathbf{\vec b} = <1+4, 2+1, 0+3>$$
$$\mathbf{\vec a}+\mathbf{\vec b} = <5, 3, 3>$$
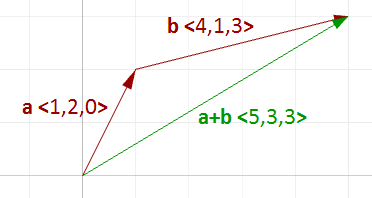
Im Allgemeinen wird die Vektoraddition der beiden Vektoren a und b wie folgt berechnet:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a}+\mathbf{\vec b} = <a_1+b_1, a_2+b_2, a_3+b_3>$$
Vektoraddition eignet sich gut, die mittlere Richtung von zwei oder mehr Vektoren zu ermitteln. In diesem Fall werden gewöhnlich Vektoren der gleichen Länge verwendet. Dieses Beispiel verdeutlicht den Unterschied zwischen der Verwendung von Vektoren der gleichen Länge und Vektoren unterschiedlicher Länge in der resultierenden Vektoraddition:
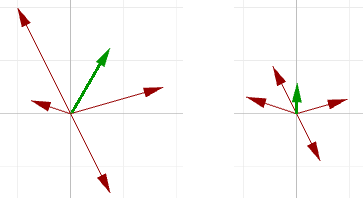
Dass Eingabevektoren die gleiche Länge haben, ist eher unwahrscheinlich. Um die mittlere Richtung zu erhalten, müssen Sie den Einheitsvektor von Eingabevektoren verwenden. Wie schon erwähnt, ist der Einheitsvektor ein Vektor, dessen Länge gleich 1 ist.
Vektorsubtraktion
Die Vektorsubtraktion geschieht anhand zweier Vektoren und ergibt einen dritten Vektor. Zwei Vektoren werden durch Subtraktion der jeweiligen Komponenten subtrahiert. Wenn wir zum Beispiel zwei Vektoren $$\mathbf{\vec a}$$ und $$\mathbf{\vec b}$$ haben und $$\mathbf{\vec b}$$ von $$\mathbf{\vec a}$$ subtrahieren, dann:
$$\mathbf{\vec a} = <1, 2, 0> $$
$$\mathbf{\vec b} = <4, 1, 4> $$
$$\mathbf{\vec a}-\mathbf{\vec b} = <1-4, 2-1, 0-4>$$
$$\mathbf{\vec a}-\mathbf{\vec b} = <-3, 1, -4> = \mathbf{\mathbf{\vec b}a}$$
Wenn wir $$\mathbf{\vec b}$$ von $$\mathbf{\vec a}$$ subtrahieren, erhalten wir ein unterschiedliches Ergebnis:
$$\mathbf{\vec b} - \mathbf{\vec a} = <4-1, 1-2, 4-0>$$
$$\mathbf{\vec b} - \mathbf{\vec a} = <3, -1, 4> = \mathbf{\mathbf{\vec a}b}$$
Beachten Sie, dass der Vektor $$\mathbf{\vec b} - \mathbf{\vec a}$$ die gleiche Länge hat wie der Vektor $$\mathbf{\vec a} - \mathbf{\vec b}$$, jedoch in entgegengesetzter Richtung.
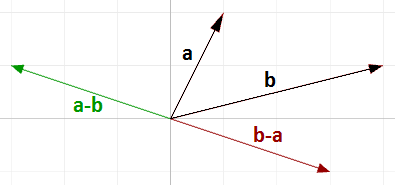
Im Allgemeinen, wenn wir zwei Vektoren $$\mathbf{\vec a}$$ und $$\mathbf{\vec b}$$ haben, dann ist $$\mathbf{\vec a} - \mathbf{\vec b}$$ ein Vektor, der wie folgt berechnet wird:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a}-\mathbf{\vec b} = <a_1 - b_1, a_2 - b_2, a_3 - b_3> = \mathbf{\mathbf{\vec b}a}$$
Vektorsubtraktion wird gewöhnlich zum Suchen von Vektoren zwischen Punkten verwendet. Wenn wir also einen Vektor suchen, der vom Endpunkt des Positionsvektors $$\mathbf{\vec b}$$ zum Endpunkt des Positionsvektors $$\mathbf{\vec a}$$ reicht, dann verwenden wir Vektorsubtraktion $$(\mathbf{\vec a}-\mathbf{\vec b})$$ wie in Abb. (11) zu sehen.
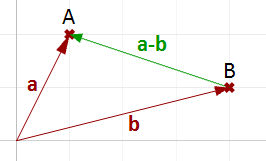
Vektoreigenschaften
Vektoren haben bis zu acht Eigenschaften. Wenn a, b und c Vektoren und s und t Zahlen sind, dann folgt:
$$\mathbf{\vec a} + \mathbf{\vec b} = \mathbf{\vec b} + \mathbf{\vec a}$$
$$\mathbf{\vec a} + 0 = a$$
$$s * (\mathbf{\vec a} + \mathbf{\vec b}) = s * a + s * \mathbf{\vec b}$$
$$s * t * (\mathbf{\vec a}) = s * (t * \mathbf{\vec a})$$
$$\mathbf{\vec a} + (\mathbf{\vec b} + \mathbf{\vec c}) = (\mathbf{\vec a} + \mathbf{\vec b}) + \mathbf{\vec c}$$
$$\mathbf{\vec a} + (-\mathbf{\vec a}) = 0$$
$$(s + t) * \mathbf{\vec a} = s * \mathbf{\vec a} + t * \mathbf{\vec a}$$
$$1 * \mathbf{\vec a} = \mathbf{\vec a}$$
Vektorpunktprodukt
Für das Punktprodukt sind zwei Vektoren nötig, und das Ergebnis ist eine Zahl. Angenommen, wir haben die beiden Vektoren a und b, so dass:
$$\mathbf{\vec a} = <1, 2, 3> $$
$$\mathbf{\vec b} = <5, 6, 7>$$
Dann ist das Punktprodukt die Summe der Multiplikation der Komponenten wie folgt:
$$\mathbf{\vec a} · \mathbf{\vec b} = 1 * 5 + 2 * 6 + 3 * 7$$
$$\mathbf{\vec a} · \mathbf{\vec b} = 38$$
Im Allgemeinen, wenn die beiden Vektoren a und b vorhanden sind:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a} · \mathbf{\vec b} = a_1 * b_1 + a_2 * b_2 + a_3 * b_3$$
Wir erhalten stets eine positive Zahl für das Punktprodukt zwischen zwei Vektoren, wenn sie in derselben allgemeinen Richtung verlaufen. Ein negatives Punktprodukt zwischen zwei Vektoren bedeutet, dass die beiden Vektoren in der entgegengesetzten allgemeinen Richtung verlaufen.
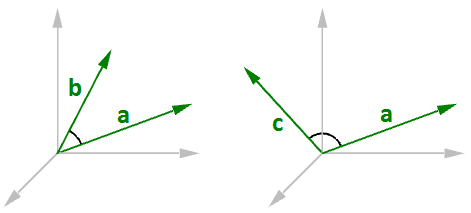
Beim Berechnen des Punktprodukts von zwei Einheitsvektoren, liegt das Ergebnis immer zwischen 1 und +1. Zum Beispiel:
$$\mathbf{\vec a} = <1, 0, 0>$$
$$\mathbf{\vec b} = <0,6, 0,8, 0>$$
$$\mathbf{\vec a} · \mathbf{\vec b} = (1 * 0.6, 0 * 0.8, 0 * 0) = 0.6$$
Außerdem ist das Punktprodukt eines Vektors mit sich selbst gleich wie die Länge dieses Vektors hoch zwei. Zum Beispiel:
$$\mathbf{\vec a} = <0, 3, 4>$$
$$\mathbf{\vec a} · \mathbf{\vec a} = 0 * 0 + 3 * 3 + 4 * 4 $$
$$\mathbf{\vec a} · \mathbf{\vec a} = 25$$
Berechnung der Länge von Vektor $$\mathbf{\vec a}$$ zum Quadrat:
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5$$
$$\vert \mathbf{\vec a} \vert 2 = 25$$
Vektorpunktprodukt, Längen und Winkel
Es besteht eine Beziehung zwischen dem Punktprodukt zweier Vektoren und dem Winkel zwischen beiden.
Generell:
$$\mathbf{\vec a} · \mathbf{\vec b} = \vert \mathbf{\vec a} \vert * \vert \mathbf{\vec b} \vert * cos(ө)$$ , oder
$$\mathbf{\vec a} · \mathbf{\vec b} / (\vert \mathbf{\vec a} \vert * \vert \mathbf{\vec b} \vert) = cos(ө)$$
Wobei:
$$ө$$ der zwischen den Vektoren enthaltene Winkel ist.
Wenn die Vektoren a und b Einheitsvektoren sind, können wir einfach sagen:
$$\mathbf{\vec a} · \mathbf{\vec b} = cos(ө)$$Und da der Kosinus eines Winkels von 90 Grad gleich 0 ist, können wir sagen:
Wenn wir beispielsweise das Punktprodukt der beiden orthogonalen Vektoren, der Welt xAchse und der yAchse berechnen, wird das Ergebnis gleich null sein.
$$\mathbf{\vec x} = <1, 0, 0>$$
$$\mathbf{\vec y} = <0, 1, 0>$$
$$\mathbf{\vec x} · \mathbf{\vec y} = (1 * 0) + (0 * 1) + (0 * 0)$$
$$\mathbf{\vec x} · \mathbf{\vec y} = 0$$
Es besteht auch eine Beziehung zwischen dem Punktprodukt und der Projektionslänge von einem Vektor auf einen anderen. Zum Beispiel:
$$\mathbf{\vec a} = <5, 2, 0>$$
$$\mathbf{\vec b} = <9, 0, 0>$$
$$Einheit(\mathbf{\vec b}) = <1, 0, 0>$$
$$\mathbf{\vec a} · Einheit(\mathbf{\vec b}) = (5 * 1) + (2 * 0) + (0 * 0) $$
$$\mathbf{\vec a} · Einheit(\mathbf{\vec b}) = 2 (\text{was gleich ist wie die Projektionslänge von mathbf{\vec a} auf mathbf{\vec b}})$$

Generell können wir mit einem gegebenen Vektor a und einem von null verschiedenen Vektor b die Projektionslänge pL von Vektor a auf Vektor b unter Verwendung des Punktprodukts berechnen.
$$pL = \vert \mathbf{\vec a} \vert * cos(ө) $$
$$pL = \mathbf{\vec a} · Einheit(\mathbf{\vec b})$$
Eigenschaften des Punktprodukts
Wenn $$\mathbf{\vec a}$$, $$\mathbf{\vec b}$$ und $$\mathbf{\vec c}$$ Vektoren sind und s eine Zahl ist, dann:
$$\mathbf{\vec a} · \mathbf{\vec a} = \vert \mathbf{\vec a} \vert ^2$$
$$\mathbf{\vec a} · (\mathbf{\vec b} + \mathbf{\vec c}) = \mathbf{\vec a} · \mathbf{\vec b} + \mathbf{\vec a} · \mathbf{\vec c}$$
$$0 · \mathbf{\vec a} = 0$$
$$\mathbf{\vec a} · \mathbf{\vec b} = \mathbf{\vec b} · \mathbf{\vec a}$$
$$(s * \mathbf{\vec a}) · \mathbf{\vec b} = s * (\mathbf{\vec a} · \mathbf{\vec b}) = \mathbf{\vec a} · (s * \mathbf{\vec b})$$
Vektor-Kreuzprodukt
Das Kreuzprodukt benötigt zwei Vektoren und ergibt einen dritten Vektor, der orthogonal zu beiden ist.
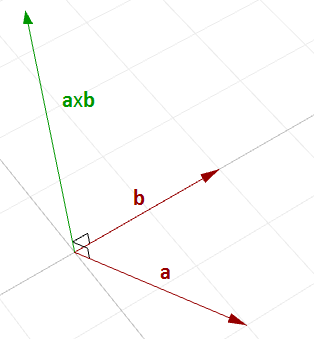
Wenn Sie zum Beispiel zwei auf der Welt-xy-Ebene liegende Vektoren haben, dann ist deren Kreuzprodukt ein Vektor, der rechtwinklig zur xy-Ebene liegt und entweder in positiver oder negativer Welt-z-Achsenrichtung verläuft. Zum Beispiel:
$$\mathbf{\vec a} = <3, 1, 0>$$
$$\mathbf{\vec b} = <1, 2, 0>$$
$$\mathbf{\vec a} × \mathbf{\vec b} = < (1 * 0 – 0 * 2), (0 * 1 - 3 * 0), (3 * 2 - 1 * 1) > $$
$$\mathbf{\vec a} × \mathbf{\vec b} = <0, 0, 5>$$
Sie werden wahrscheinlich nie von Hand ein Kreuzprodukt von zwei Vektoren berechnen müssen. Wenn Sie die Vorgehensweise trotzdem interessiert, lesen Sie weiter; ansonsten können Sie diesen Abschnitt einfach überspringen. Das Kreuzprodukt $$a × b$$ wird durch die Verwendung von Determinanten bestimmt. Was folgt ist eine einfache Veranschaulichung, wie eine Determinante unter Verwendung der Standard-Basisvektoren berechnet wird:
$$ \color {red}{i} = <1, 0, 0>$$
$$ \color {blue}{j} = <0,1, 0>$$
$$ \color {green}{k} = <0, 0, 1>$$
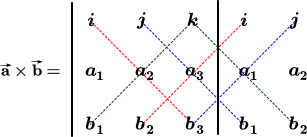
Das Kreuzprodukt der beiden Vektoren $$\mathbf{\vec a} = <a1, a2, a3>$$ und $$\mathbf{\vec b} = <b1, b2, b3>$$ wird wie folgt unter Verwendung des obigen Diagramms berechnet:
$$\mathbf{\vec a} × \mathbf{\vec b} = \color {red}{i (a_2 * b_3)} + \color {blue}{ j (a_3 * b_1)} + \color {green}{k(a_1 * b_2)} - \color {green}{k (a_2 * b_1)} - \color {red}{i (a_3 * b_2)} -\color {blue}{ j (a_1 * b_3)}$$
$$\mathbf{\vec a} × \mathbf{\vec b} = \color {red}{i (a_2 * b_3 - a_3 * b_2)} + \color {blue}{j (a_3 * b_1 - a_1 * b_3)} +\color {green}{k (a_1 * b_2 - a_2 * b_1)}$$
$$\mathbf{\vec a} × \mathbf{\vec b} = <\color {red}{a_2 * b_3 – a_3 * b_2}, \color {blue}{a_3 * b_1 - a_1 * b_3}, \color {green}{a_1 * b_2 - a_2 * b_1} >$$
Kreuzprodukte und Winkel zwischen Vektoren
Zwischen dem Winkel zwischen zwei Vektoren und der Länge ihres Kreuzproduktvektors besteht eine Beziehung. Je kleiner der Winkel (kleinerer Sinus), desto kürzer ist der Vektor des Kreuzprodukts. Die Reihenfolge der Operanden ist im Kreuzprodukt eines Vektors von Bedeutung. Zum Beispiel:
$$\mathbf{\vec a} = <1, 0, 0>$$
$$\mathbf{\vec b} = <0, 1, 0>$$
$$\mathbf{\vec a} × \mathbf{\vec b} = <0, 0, 1>$$
$$\mathbf{\vec b} × \mathbf{\vec a} = <0, 0, -1>$$
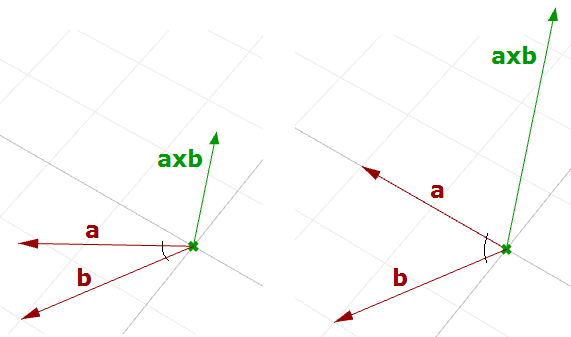
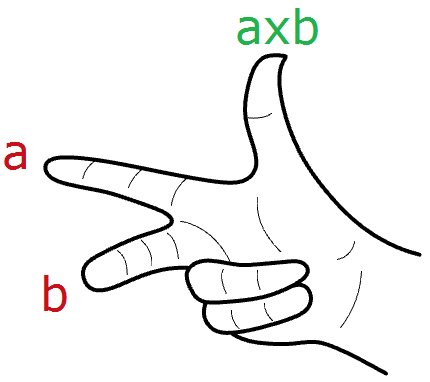
In Rhinos rechtshändig ausgelegtem System wird die Richtung von $$\mathbf{\vec a} × \mathbf{\vec b}$$ durch die Dreifingerregel bestimmt ( $$\mathbf{\vec a}$$ = Zeigefinger, $$\mathbf{\vec b}$$ = Mittelfinger und $$\mathbf{\vec a} × \mathbf{\vec b}$$ = Daumen).
Generell, für ein beliebiges Paar von 3D-Vektoren $$\mathbf{\vec a}$$ und $$\mathbf{\vec b}$$:
$$$vert \mathbf{\vec a} × \mathbf{\vec b} \vert = \vert \mathbf{\vec a} \vert \vert \mathbf{\vec b} \vert sin(ө)$$Wobei:
$$ө$$ der zwischen den Positionsvektoren von $$\mathbf{\vec a}$$ und $$\mathbf{\vec b}$$ enthaltene Winkel ist.
Wenn a und b Einheitsvektoren sind, können wir ebenso gut sagen, dass die Länge ihres Kreuzprodukts gleichwertig mit dem Sinus des Winkels zwischen ihnen ist. Anders ausgedrückt:
$$\vert \mathbf{\vec a} × \mathbf{\vec b} \vert = sin(ө)$$Das Kreuzprodukt zwischen zwei Vektoren hilft uns dabei zu bestimmen, ob zwei Vektoren parallel sind. Der Grund dafür ist, dass das Ergebnis immer ein Nullvektor ist.
Eigenschaften des Kreuzprodukts
Wenn
$$\mathbf{\vec a}$$,
$$\mathbf{\vec b}$$, and
$$\mathbf{\vec c}$$ Vektoren sind und
$$s$$ eine Zahl, dann:
$$\mathbf{\vec a} × \mathbf{\vec b} = -\mathbf{\vec b} × \mathbf{\vec a}$$
$$(s * \mathbf{\vec a}) × \mathbf{\vec b} = s * (\mathbf{\vec a} × \mathbf{\vec b}) = \mathbf{\vec a} × (s * \mathbf{\vec b})$$
$$\mathbf{\vec a} × (\mathbf{\vec b} + \mathbf{\vec c}) = \mathbf{\vec a} × \mathbf{\vec b} + \mathbf{\vec a} × \mathbf{\vec c}$$
$$(\mathbf{\vec a} + \mathbf{\vec b}) × \mathbf{\vec c} = \mathbf{\vec a} × \mathbf{\vec c} + \mathbf{\vec b} × \mathbf{\vec c}$$
$$\mathbf{\vec a} · (\mathbf{\vec b} × \mathbf{\vec c}) = (\mathbf{\vec a} × \mathbf{\vec b}) · \mathbf{\vec c}$$
$$\mathbf{\vec a} × (\mathbf{\vec b} × \mathbf{\vec c}) = (\mathbf{\vec a} · \mathbf{\vec c}) * \mathbf{\vec b} – (\mathbf{\vec a} · \mathbf{\vec b}) * \mathbf{\vec c}$$
1.3 Lineare Vektorgleichungen
Die lineare Vektorgleichung wird in Anwendungen für die 3D-Modellierung und für Computergrafiken verwendet.
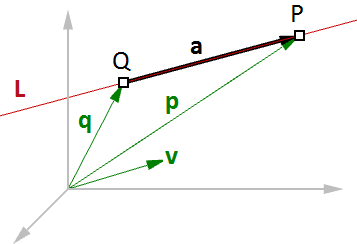
Wenn wir etwa die Richtung einer Linie und einen Punkt auf dieser Linie kennen, dann können wir unter Verwendung von Vektoren auch jeden anderen Punkt auf dieser Linie finden, wie im folgenden Beispiel:
$$\overline{L} = Linie$$
$$\mathbf{\vec v} = <a, b, c>$$ Linienrichtung-Einheitsvektor
$$Q = (x_0, y_0, z_0)$$ Linienstandortpunkt
$$P = (x, y, z)$$ Jeder beliebiger Punkt auf der Linie
Wir wissen, dass:
$$\mathbf{\vec a} = t *\mathbf{\vec v}$$ (2)
$$\mathbf{\vec p} = \mathbf{\vec q} + \mathbf{\vec a}$$ (1)
Von 1 und 2:
$$\mathbf{\vec p} = \mathbf{\vec q} + t * \mathbf{\vec v}$$ (3)
Allerdings können wir (3) auch wie folgt schreiben:
$$<x, y, z> = <x_0, y_0, z_0> + <t * a, t * b, t * c>$$
$$<x, y, z> = <x_0 + t * a, y_0 + t * b, z_0 + t * c>$$
Daher:
$$x = x_0 + t * a$$
$$y = y_0 + t * b$$
$$z = z_0 + t * c$$
Was auf das Gleiche herauskommt wie:
$$P = Q + t * \mathbf{\vec v}$$Ein ebenfalls häufiges Beispiel ist das Auffinden des Mittelpunkts zwischen zwei Punkten. Im Folgenden ist zu sehen, wie der Mittelpunkt unter Verwendung der Vektorgleichung einer Linie zu finden ist:
$$\mathbf{\vec q}$$ ist der Standortvektor für Punkt
$$Q$$
$$\mathbf{\vec p}$$ ist der Standortvektor für Punkt
$$P$$
$$\mathbf{\vec a}$$ ist der
$$Q \rightarrow P$$ verlaufende Vektor
Anhand der Vektorsubtraktion wissen wir, dass:
$$\mathbf{\vec a} = \mathbf{\vec p} - \mathbf{\vec q}$$Anhand der linearen Gleichung wissen wir, dass:
$$M = Q + t * \mathbf{\vec a}$$Und da wir den Mittelpunkt finden müssen, folgt:
$$t = 0.5$$Daher können wir sagen:
$$M = Q + 0.5 * \mathbf{\vec a}$$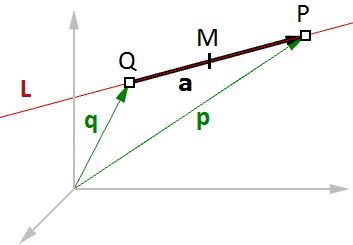
Im Allgemeinen können Sie jeden beliebigen Punkt zwischen $$Q$$ und $$P$$ finden, und zwar indem Sie den Wert $$t$$ zwischen 0 und 1 ändern, bei Anwendung der allgemeinen Gleichung:
$$M = Q + t * (P - Q)$$1.4 Vektorgleichung einer Ebene
Eine Möglichkeit zum Bestimmen einer Ebene besteht, wenn Sie einen Punkt haben und einen Vektor, der sich rechtwinklig zur Ebene befindet. Dieser Vektor wird üblicherweise als normal zur Ebene bezeichnet. Die normalen Punkte in der Richtung über der Ebene.
Eine Ebenennormale ist beispielsweise auch zu berechnen, wenn uns drei nicht-lineare Punkte auf der Ebene bekannt sind.
In Abb. (16) haben wir:
$$A$$ = der erste Punkt auf der Ebene
$$B$$ = der zweite Punkt auf der Ebene
$$C$$ = der dritte Punkt auf der Ebene
Sowie:
$$\mathbf{\vec a} $$ = ein Positionsvektor des Punktes
$$A$$
$$\mathbf{\vec b}$$ = ein Positionsvektor des Punktes
$$B$$
$$\mathbf{\vec c}$$ = ein Positionsvektor des Punktes
$$C$$
Der Normalenvektor $$\mathbf{\vec n}$$ ist folgendermaßen zu finden:
$$\mathbf{\vec n} = (\mathbf{\vec b} - \mathbf{\vec a}) × (\mathbf{\vec c} - \mathbf{\vec a})$$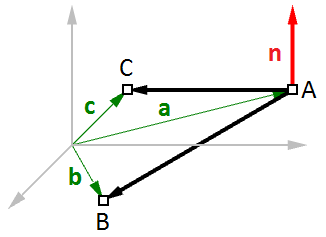
Wir können die skalare Gleichung der Ebene auch unter Verwendung des Vektorpunktprodukts ableiten:
$$\mathbf{\vec n} · (\mathbf{\vec b} - \mathbf{\vec a}) = 0$$Wenn:
$$\mathbf{\vec n} = <a, b, c>$$
$$\mathbf{\vec b} = <x, y, z>$$
$$ \mathbf{\vec a} = <x_0, y_0, z_0>$$
Das Obenstehende können wir dann erweitern:
$$<a, b, c> · <x-x_0, y-y_0, z-z_0 > = 0$$Die Auflösung des Punktprodukts erbringt die allgemeine skalare Gleichung einer Ebene:
$$a * (x - x_0) + b * (y - y_0) + c * (z - z_0) = 0$$1.5 Tutorials
Alle in diesem Kapitel besprochenen Konzepte können direkt zur Lösung während des Modellierens häufig auftauchender Probleme angewendet werden. Die Folgenden sind Schritt-für-Schritt-Tutorials, welche die in diesem Kapitel erlernten Konzepte unter Verwendung von Rhinoceros und Grasshopper (GH) anwenden.
1.5.1 Seitenrichtung
Angenommen, wir haben einen Punkt und eine Fläche; wie können wir dann bestimmen, ob der Punkt der Vorder- oder Rückseite dieser Fläche zugewandt ist?
Eingabe:
- eine Fläche
- ein Punkt
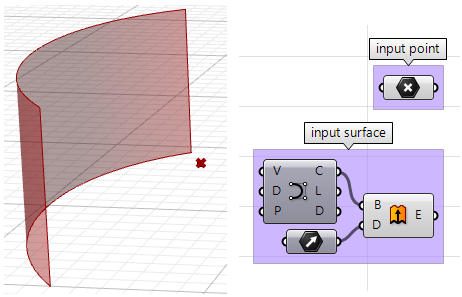
Parameter:
Die Seitenrichtung ist durch die Normalenrichtung der Fläche gegeben. Wir benötigen die folgenden Informationen:
- Die Normalenrichtung der Fläche auf einem Flächenstandort möglichst nahe am Eingabepunkt.
- Eine Vektorrichtung vom nächstmöglichen Punkt zum Eingabepunkt.
Vergleichen Sie beiden oben genannten Richtungen: wenn die Richtung gleich ist, ist der Punkt der Vorderseite zugewandt, und andernfalls der Rückseite.
Lösung:
1. Suchen Sie auf der Fläche den Punktstandort, der am nächsten zum Eingabepunkt liegt, und zwar mittels der Komponente Pull. Daraus ergibt sich für uns der uv-Standort des nächstgelegenen Punkts, den wir dann zur Auswertung der Fläche und zum Finden ihrer Normalenrichtung verwenden können.
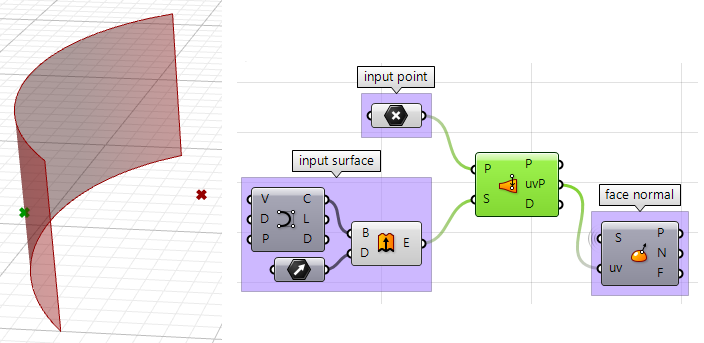
2. Jetzt können wir den nächstgelegenen Punkt verwenden, um einen zum Eingabepunkt verlaufenden Vektor zu zeichnen. Wir können auch folgendes zeichnen:
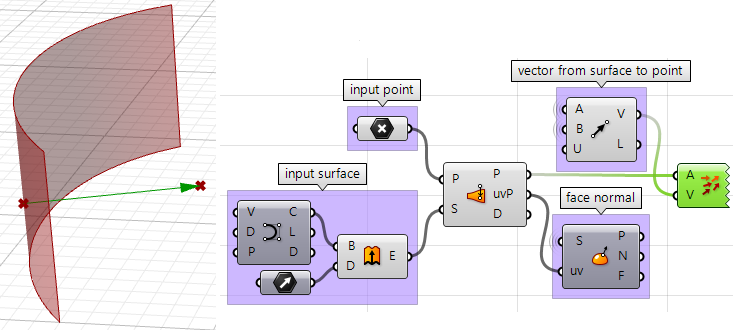
3. Wir können die beiden Vektoren unter Verwendung des Punktprodukts vergleichen. Fällt das Ergebnis positiv aus, befindet sich der Punkt vor der Fläche. Fällt es negativ aus, befindet sich der Punkt hinter der Fläche.
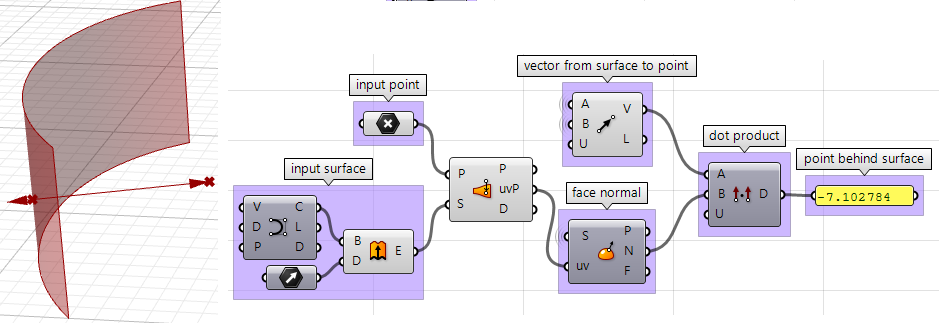
Der obige Schritt kann auch unter Verwendung anderer Scripting-Sprachen gelöst werden. Unter Verwendung der Grasshopper-VB-Komponente:
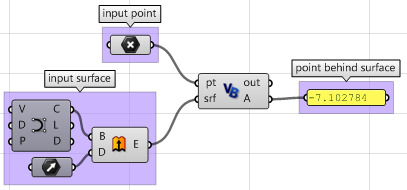
Private Sub RunScript(ByVal pt As Point3d, ByVal srf As Surface, ByRef A As Object)
'Declare variables
Dim u, v As Double
Dim closest_pt As Point3d
'get closest point u, v
srf.ClosestPoint(pt, u, v)
'get closest point
closest_pt = srf.PointAt(u, v)
'calculate direction from closest point to test point
Dim dir As New Vector3d(pt - closest_pt)
'calculate surface normal
Dim normal = srf.NormalAt(u, v)
'compare the two directions using the dot product
A = dir * normal
End Sub
Unter Verwendung der Grasshopper-Python-Komponente mit RhinoScriptSyntax:
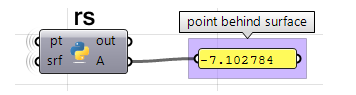
import rhinoscriptsyntax as rs #import RhinoScript library
#find the closest point
u, v = rs.SurfaceClosestPoint(srf, pt)
#get closest point
closest_pt = rs.EvaluateSurface(srf, u, v)
#calculate direction from closest point to test point
dir = rs.PointCoordinates(pt) - closest_pt
#calculate surface normal
normal = rs.SurfaceNormal(srf, [u, v])
#compare the two directions using the dot product
A = dir * normal
Unter Verwendung der Grasshopper-Python-Komponente nur mit RhinoCommon:
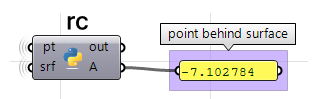
#find the closest point
found, u, v = srf.ClosestPoint(pt)
if found:
#get closest point
closest_pt = srf.PointAt(u, v)
#calculate direction from closest point to test point
dir = pt - closest_pt
#calculate surface normal
normal = srf.NormalAt(u, v)
#compare the two directions using the dot product
A = dir * normal
Unter Verwendung der Grasshopper-C#-Komponente:

private void RunScript(Point3d pt, Surface srf, ref object A)
{
//Declare variables
double u, v;
Point3d closest_pt;
//get closest point u, v
srf.ClosestPoint(pt, out u, out v);
//get closest point
closest_pt = srf.PointAt(u, v);
//calculate direction from closest point to test point
Vector3d dir = pt - closest_pt;
//calculate surface normal
Vector3d normal = srf.NormalAt(u, v);
//compare the two directions using the dot product
A = dir * normal;
}
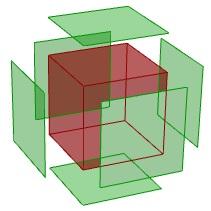
1.5.2 Zerlegter Quader
Im folgenden Tutorial wird das Zerlegen eines Flächenverbandes gezeigt. So sieht der zerlegte Quader am Ende aus:
Eingabe:
Identifizierung der Eingabe, die ein Quader ist. Wir verwenden den Quader-Parameter in GH:

Parameter:
- Bedenken Sie alle Parameter, die zur Bewältigung dieses Tutorials bekannt sein müssen.
- Das Zentrum der Zerlegung.
- Die zu zerlegenden Quaderseiten.
- Die Richtung, in die sich jede Seite bewegt.
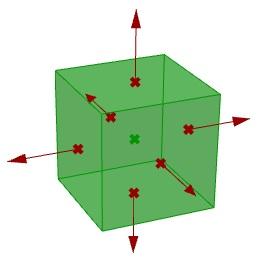
Sobald die Parameter identifiziert sind, geht es darum, anhand logischer Schritte eine Lösung zu finden.
Lösung:
1. Finden Sie das Zentrum des Quaders mithilfe der Komponente Box Properties in GH:
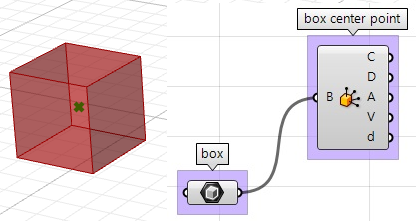
2. Extrahieren Sie die Quaderseiten mit der Komponente Deconstruct Brep:
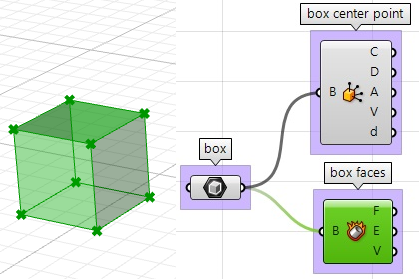
3. Die Richtung, in der wir die Seiten verschieben, ist am heikelsten. Zuerst müssen wir die Mitte jeder Seite finden, um dann die Richtung vom Zentrum des Quaders aus zur Mitte jeder Seite hin zu bestimmen, und zwar folgendermaßen:
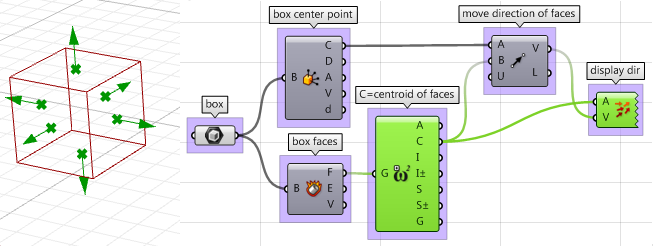
4. Sobald wir alle Parameter gescriptet haben, können wir die Komponente Move benutzen, um die Seiten in der benötigten Richtung zu verschieben. Vergewissern Sie sich lediglich, dass die Vektoren auf die richtige Weite eingestellt sind, um fortfahren zu können.
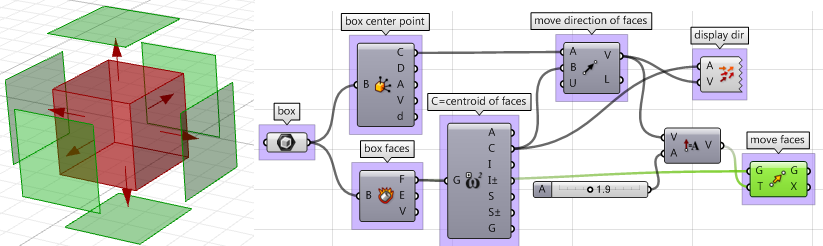
Die obigen Schritte können auch unter Verwendung von VB Script, C# oder Python bewältigt werden. Was folgt, ist die Lösung unter Verwendung dieser Scripting-Sprachen.
Unter Verwendung der Grasshopper-VB-Komponente:
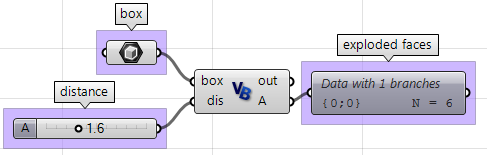
Private Sub RunScript(ByVal box As Brep, ByVal dis As Double, ByRef A As Object)
'get the brep center
Dim area As Rhino.Geometry.AreaMassProperties
area = Rhino.Geometry.AreaMassProperties.Compute(box)
Dim box_center As Point3d
box_center = area.Centroid
'get a list of faces
Dim faces As Rhino.Geometry.Collections.BrepFaceList = box.Faces
'decalre variables
Dim center As Point3d
Dim dir As Vector3d
Dim exploded_faces As New List( Of Rhino.Geometry.Brep )
Dim i As Int32
'loop through all faces
For i = 0 To faces.Count() - 1
'extract each of the face
Dim extracted_face As Rhino.Geometry.Brep = box.Faces.ExtractFace(i)
'get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face)
center = area.Centroid
'calculate move direction (from box centroid to face center)
dir = center - box_center
dir.Unitize()
dir *= dis
'move the extracted face
extracted_face.Transform(Transform.Translation(dir))
'add to exploded_faces list
exploded_faces.Add(extracted_face)
Next
'assign exploded list of faces to output
A = exploded_faces
End Sub
Unter Verwendung der Grasshopper-Python-Komponente mit RhinoCommon:
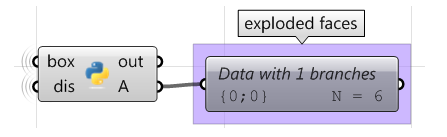
import Rhino
#get the brep center
area = Rhino.Geometry.AreaMassProperties.Compute(box)
box_center = area.Centroid
#get a list of faces
faces = box.Faces
#decalre variables
exploded_faces = []
#loop through all faces
for i, face in enumerate(faces):
#get a duplicate of the face
extracted_face = faces.ExtractFace(i)
#get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face)
center = area.Centroid
#calculate move direction (from box centroid to face center)
dir = center - box_center
dir.Unitize()
dir *= dis
#move the extracted face
move = Rhino.Geometry.Transform.Translation(dir)
extracted_face.Transform(move)
#add to exploded_faces list
exploded_faces.append(extracted_face)
#assign exploded list of faces to output
A = exploded_faces
Unter Verwendung der Grasshopper-C#-Komponente:
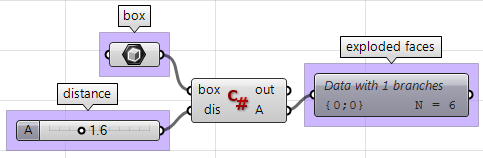
private void RunScript(Brep box, double dis, ref object A)
{
//get the brep center
Rhino.Geometry.AreaMassProperties area = Rhino.Geometry.AreaMassProperties.Compute(box);
Point3d box_center = area.Centroid;
//get a list of faces
Rhino.Geometry.Collections.BrepFaceList faces = box.Faces;
//decalre variables
Point3d center; Vector3d dir;
List<Rhino.Geometry.Brep> exploded_faces = new List<Rhino.Geometry.Brep>();
//loop through all faces for( int i = 0; i < faces.Count(); i++ )
{
//extract each of the face
Rhino.Geometry.Brep extracted_face = box.Faces.ExtractFace(i);
//get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face);
center = area.Centroid;
//calculate move direction (from box centroid to face center)
dir = center - box_center;
dir.Unitize();
dir *= dis;
//move the extracted face
extracted_face.Transform(Transform.Translation(dir));
//add to exploded_faces list
exploded_faces.Add(extracted_face);
}
//assign exploded list of faces to output
A = exploded_faces;
}
1.5.3 Tangentiale Kugeln
In diesem Tutorial lernen wir, zwei tangentiale Kugeln zwischen zwei Eingabepunkten zu erzeugen. Das Ergebnis sieht so aus:
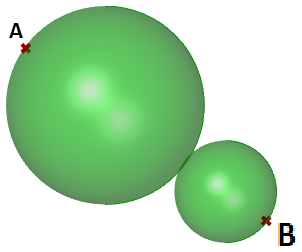
Eingabe:
Zwei Punkte (
$$A$$ und
$$B$$) im 3D-Koordinatensystem.
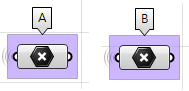
Parameter: Was folgt, ist ein Diagramm der zur Lösung des Problems benötigten Parameter:
ein tangentialer Punkt $$D$$ zwischen den beiden Kugeln, an einem $$t$$-Parameter (0-1) zwiwchen den Punkten $$A$$ und $$B$$.
- Das Zentrum der ersten Kugel oder der Mittelpunkt $$C1$$ zwischen $$A$$ und $$D$$.
- Das Zentrum der zweiten Kugel oder der Mittelpunkt $$C2$$ zwischen $$D$$ und $$B$$.
- Der Radius der ersten Kugel $$(r1)$$ oder der Abstand zwischen $$A$$ und $$C1$$.
- Der Radius der zweiten Kugel $$(r2)$$ oder der Abstand zwischen $$D$$ und $$C2$$.
Lösung:
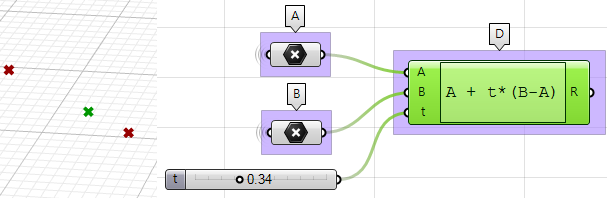
1. Verwenden Sie die Komponente Expression, um den Punkt $$D$$ zwischen $$A$$ und $$B$$ an einem Parameter $$t$$ zu bestimmen. Die von uns verwendete Expression basiert auf der Vektorgleichung einer Linie:
$$D = A + t*(B-A)$$
$$B-A$$ ist der Vektor, der bei Anwendung der Vektorsubtraktion von $$B$$ nach $$A$$ verläuft.
$$t*(B-A)$$ : wobei
$$t$$zwischen 0 und 1 liegt, damit wir einen Standort auf dem Vektor erhalten.
$$A+t*(B-A)$$ : liefert einen Punkt auf dem Vektor zwischen A und B.
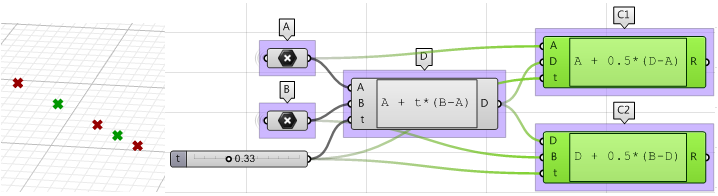
2. Verwenden Sie die Komponente Expression um auch die Mittelpunkte
$$C1$$ und$$C2$$zu bestimmen.
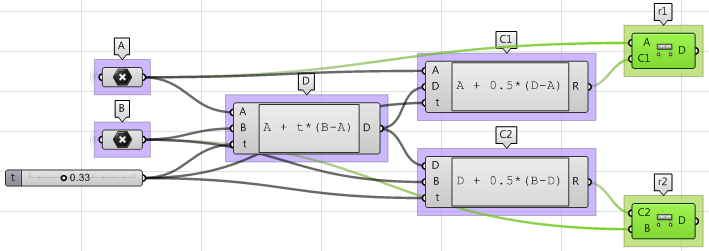
3. Der erste Kugelradius
$$(r1)$$ und der zweite Kugelradius$$(r2)$$kann unter Verwendung der Komponente Distance berechnet werden.
4. Im letzten Schritt geht es um die Erzeugung der Kugel anhand einer Basisfläche und eines Radius. Wir müssen sicherstellen, dass die Ursprünge auf
$$C1$$ und$$C2$$ festgelegt sind sowie den Radius von$$r1$$ und$$r2$$.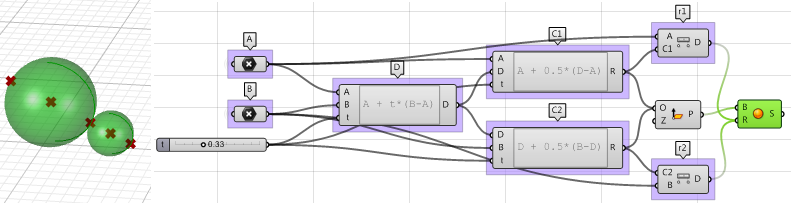
Unter Verwendung der Grasshopper-VB-Komponente:
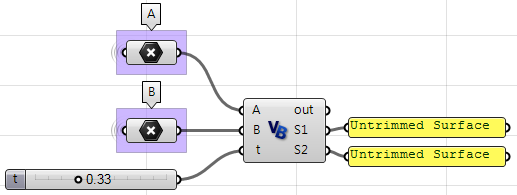
Private Sub RunScript(ByVal A As Point3d, ByVal B As Point3d, ByVal t As Double, ByRef S1 As Object, ByRef S2 As Object)
'declare variables
Dim D, C1, C2 As Rhino.Geometry.Point3d
Dim r1, r2 As Double
'find a point between A and B
D = A + t * (B - A)
'find mid point between A and D
C1 = A + 0.5 * (D - A)
'find mid point between D and B
C2 = D + 0.5 * (B - D)
'find spheres radius
r1 = A.DistanceTo(C1)
r2 = B.DistanceTo(C2)
'create spheres and assign to output
S1 = New Rhino.Geometry.Sphere(C1, r1)
S2 = New Rhino.Geometry.Sphere(C2, r2)
End Sub
Unter Verwendung der Python-Komponente:
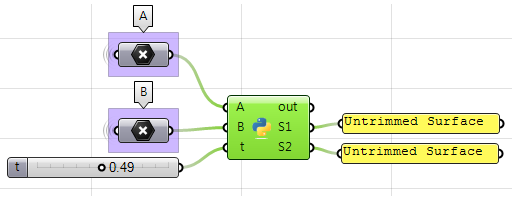
import Rhino
#find a point between A and B
D = A + t * (B - A)
#find mid point between A and D
C1 = A + 0.5 * (D - A)
#find mid point between D and B
C2 = D + 0.5 * (B - D)
#find spheres radius
r1 = A.DistanceTo(C1)
r2 = B.DistanceTo(C2)
#create spheres and assign to output
S1 = Rhino.Geometry.Sphere(C1, r1)
S2 = Rhino.Geometry.Sphere(C2, r2)
Unter Verwendung der Grasshopper-C#-Komponente:
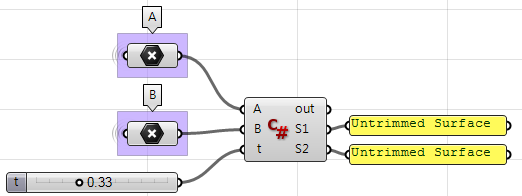
private void RunScript(Point3d A, Point3d B, double t, ref object S1, ref object S2)
{
//declare variables
Rhino.Geometry.Point3d D, C1, C2;
double r1, r2;
//find a point between A and B
D = A + t * (B - A);
//find mid point between A and D
C1 = A + 0.5 * (D - A);
//find mid point between D and B
C2 = D + 0.5 * (B - D);
//find spheres radius
r1 = A.DistanceTo(C1);
r2 = B.DistanceTo(C2);
//create spheres and assign to output
S1 = new Rhino.Geometry.Sphere(C1, r1);
S2 = new Rhino.Geometry.Sphere(C2, r2);
}
Beispieldateien herunterladen
Laden Sie das Archiv download samplesand tutorials herunter, das alle Grasshopper-Beispiele und Codedateien in diesem Handbuch enthält.
Weitere Schritte:
Nun, da Sie die Vektor-Mathematik kennen, sehen Sie sich den Leitfaden Matrices und Transformationen an, um mehr über das Verschieben, Drehen und Skalieren von Objekten zu lernen..

