Transformaciones hace referencia a operaciones como mover (denominado también traslación), rotar y escalar objetos. En programación 3D se almacenan utilizando matrices, que son series rectangulares de números. Se pueden realizar múltiples transformaciones rápidamente utilizando matrices. Una matriz [[4x4]] puede representar todas las transformaciones. Tener una dimensión de matriz unificada para todas las transformaciones ahorra tiempo de cálculo.
$$\begin{array}{rcc} \mbox{matrix}&\begin{array}{cccc} c1& c2&c3&c4\end{array}\\\begin{array}{c}row(1)\\row(2)\\row(3)\\row(4)\end{array}& \left[\begin{array}{cr} +&+&+&+\\ +&+&+&+\\ +&+&+&+\\ +&+&+&+\end{array}\right] \end{array}$$2.1 Operaciones con matrices
La operación más relevante en el diseño gráfico por ordenador es la multiplicación de matrices. Ahora lo explicamos con más detalle.
Multiplicación de matrices
La multiplicación de matrices se utiliza para aplicar transformaciones a la geometría. Por ejemplo, si tenemos un punto y queremos rotarlo alrededor de un eje, usamos una matriz de rotación y la multiplicamos por el punto para obtener la nueva ubicación rotada.
$$\begin{array}{ccc} \text{rotate matrix} & \text{input point} & \text{rotate point}\\\begin{bmatrix}a & b & c & d \\e & f & g & h \\i & j & k & l \\0 & 0 & 0 & 1 \\\end{bmatrix}& \cdot\begin{bmatrix}x \\y\\z\\1 \\\end{bmatrix}&= \begin{bmatrix}x' \\y'\\z'\\1 \\\end{bmatrix}\end{array}$$La mayoría de las veces, necesitamos realizar múltiples transformaciones en la misma geometría. Por ejemplo, si necesitamos mover y rotar mil puntos, podemos usar cualquiera de los siguientes métodos.
Método 1
- Multiplique la matriz de movimiento por 1000 puntos para mover los puntos.
- Multiplique la matriz de rotación por los 1000 puntos resultantes para rotar los puntos movidos.
Número de operaciones =2000.
Método 2
- Multiplique las matrices de rotación y movimiento para crear una matriz de transformación combinada.
- Multiplique la matriz combinada por 1000 puntos para mover y rotar en un solo paso.
Número de operaciones =1001.
Observe que el método 1 requiere casi el doble de operaciones para lograr el mismo resultado. Si bien el método 2 es muy eficaz, solo es posible si las matrices de movimiento y rotación son $$[4 \times 4]$$. Por este motivo, en el diseño gráfico por ordenador se usa una matriz $$[4 \times 4]$$ para representar todas las transformaciones, y una matriz $$[4 \times 1]$$ para representar puntos.
Las aplicaciones de modelado tridimensional proporcionan herramientas para aplicar transformaciones y multiplicar matrices, pero si tiene curiosidad sobre cómo multiplicar matrices matemáticamente, le explicaremos un ejemplo sencillo. Para multiplicar dos matrices, éstas tienen que coincidir. En otras palabras, el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz. La matriz resultante tiene un tamaño igual al número de filas de la primera matriz y al número de columnas de la segunda matriz. Por ejemplo, si tenemos dos matrices, $$M$$ y $$P$$, con tamaños igual a $$[4\times 4]$$ and $$[4 \times 1]$$ respectivamente, la matriz de multiplicación resultante $$M · P$$ tiene un tamaño igual a $$[4 \times 1]$$, como se muestra en la siguiente ilustración:
$$\begin{array}{ccc} M & P & P' \\\begin{bmatrix}\color{red}{a} & \color{red}{b} & \color{red}{c} & \color{red}{d} \\e & f & g & h \\i & j & k & l \\0 & 0 & 0 & 1 \\\end{bmatrix}& \cdot\begin{bmatrix}\color{red}{x} \\\color{red}{y} \\\color{red}{z} \\\color{red}{1} \\\end{bmatrix}&= \begin{bmatrix}\color{red}{x'=a*x+b*y+c*z+d*1}\\y'=e*x+f*y+g*z+h*1\\z'=i*x+j*y+k*z+l*1 \\1=0*x+0*y+0*z+1*1\\\end{bmatrix}\end{array}$$Matriz de identidad
La matriz de identidad es una matriz especial donde todos los componentes diagonales son iguales a 1 y el resto igual a 0.
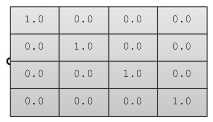
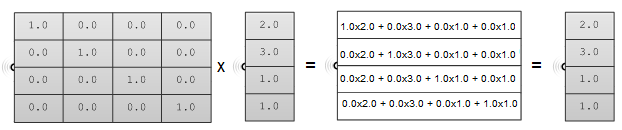
La propiedad principal de la matriz identidad es que si se multiplica por cualquier otra matriz, los valores multiplicados por cero no cambian.
2.2 Operaciones de transformación
La mayoría de las transformaciones conservan la relación paralela entre las partes de la geometría. Por ejemplo, los puntos colineales permanecen colineales después de la transformación. También los puntos de un plano permanecen coplanares después de la transformación. Este tipo de transformación se denomina transformacion afin.
Traslación (mover)
Mover un punto desde una posición inicial a lo largo de un vector determinado se calcula de la siguiente manera:
$$P’ = P + \mathbf{\vec v}$$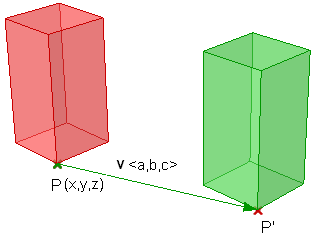
Supongamos que:
$$P(x,y,z)$$ es un punto dado
$$\mathbf{\vec v}=<a,b,c>$$ es un vector de traslación
Entonces:
$$P’(x) = x + a$$
$$P’(y) = y + b$$
$$P’(z) = z + c$$
Los puntos se representan en un formato de matriz utilizando una matriz [4x1] con un 1 insertado en la última fila. Por ejemplo, el punto P (x,y,z) se representa de la siguiente manera:
$$\begin{bmatrix}x\\y\\z\\1\\\end{bmatrix}$$El uso de una matriz $$[4 \times 4]$$ para las transformaciones (lo que se denomina un sistema de coordenadas homogéneo) en lugar una matriz $$[3 \times 3]$$, permite representar todas las transformaciones, incluida la traslación. El formato general de una matriz de traslación es:
$$\begin{bmatrix}1 & 0 & 0 & \color{red}{a1} \\0 & 1 & 0 & \color{red}{a2} \\0 & 0 & 1 & \color{red}{a3} \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Por ejemplo, para mover el punto $$P(2,3,1)$$ por el vector $$\vec v <2,2,2>$$, la nueva ubicación del punto es:
$$P’ = P + \mathbf{\vec v} = (2+2, 3+2, 1+2) = (4, 5, 3)$$Si empleamos las matrices y multiplicamos la matriz de traslación por el punto de entrada, obtenemos la nueva ubicación del punto como se muestra a continuación:
$$\begin{bmatrix}1 & 0 & 0 & 2 \\0 & 1 & 0 & 2 \\0 & 0 & 1 & 2 \\0 & 0 & 0 & 1 \\\end{bmatrix}\cdot\begin{bmatrix}2 \\3\\1\\1 \\\end{bmatrix}= \begin{bmatrix}(1*2 + 0*3 + 0*1 + 2*1) \\(0*2 + 1*3 + 0*1 + 2*1)\\(0*2 + 0*3 + 1*1 + 2*1)\\(0*2 + 0*3 + 0*1 + 1*1)\\\end{bmatrix}=\begin{bmatrix}4 \\5\\3\\1 \\\end{bmatrix}$$De manera similar, cualquier geometría se traslada multiplicando sus puntos de construcción por la matriz de traslación. Por ejemplo, si tenemos una caja definida por ocho puntos de esquina y queremos moverla 4 unidades en la dirección x, 5 unidades en la dirección y, y 3 unidades en la dirección z, debemos multiplicar cada uno de los ocho puntos de esquina de la caja por la siguiente matriz de traslación para obtener la nueva caja.
$$\begin{bmatrix}1 & 0 & 0 & 4\\ 0 & 1 & 0 & 5 \\0 & 0 & 1 & 3 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$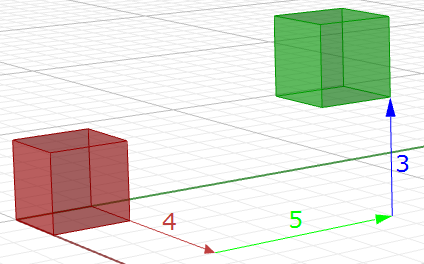
Rotación
Esta sección muestra cómo calcular la rotación alrededor del eje z y el punto de origen utilizando la trigonometría, y luego deducir el formato general de la matriz para la rotación.
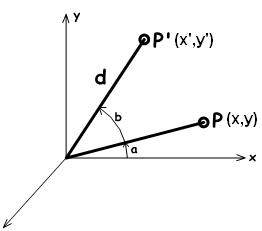
Tome un punto en el plano $$x,y$$ $$P(x,y)$$ y gírelo un ángulo ( $$b$$). Del resultado, podemos deducir lo siguiente:
$$x = d cos(a)$$ (1)
$$y = d sin(a)$$ (2)
$$x’ = d cos(b+a)$$ (3)
$$y’ = d sin(b+a)$$ (4)
Podemos expandir
$$x$$’ e
$$y’$$ usando las identidades trigonométricas del seno y el coseno de la suma de ángulos:
$$x’ = d cos(a)cos(b) - d sin(a)sin(b)$$ (5)
$$y’ = d cos(a)sin(b) + d sin(a)cos(b)$$ (6)
Usando las ecuaciones 1 y 2:
$$x’ = x cos(b) - y sin(b)$$
y’ = x sin(b) + y cos(b)
La matriz de rotación alrededor del eje z quedaría así:
$$\begin{bmatrix}\color{red}{\cos{b}} & \color{red}{-\sin{b}} & 0 & 0 \\\color{red}{\sin{b}} & \color{red}{\cos{b}} & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$La matriz de rotación alrededor del eje x por el ángulo $$b$$ quedaría así:
$$\begin{bmatrix}1 & 0 & 0 & 0 \\0 & \color{red}{\cos{b}} & \color{red}{-\sin{b}} & 0 \\0 & \color{red}{\sin{b}} & \color{red}{\cos{b}} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$La matriz de rotación alrededor del eje y por el ángulo $$b$$ quedaría así:
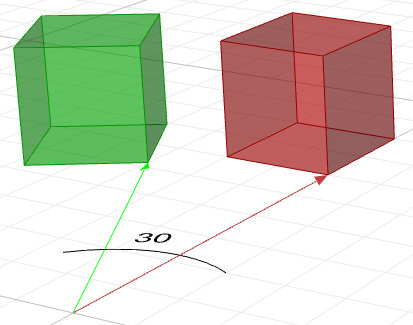
$$\begin{bmatrix}\color{red}{\cos{b}} &0 & \color{red}{\sin{b}} & 0 \\0 & 1 & 0 & 0 \\\color{red}{-\sin{b}} & 0 &\color{red}{\cos{b}} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Por ejemplo, si tenemos una caja y queremos rotarla 30 grados, necesitamos lo siguiente:
1. Construya la matriz de rotación de 30 grados. Utilizando la forma genérica y los valores de coseno y seno del ángulo de 30 grados, la matriz de rotación quedaría así:
$$\begin{bmatrix}0.87 & -0.5 & 0 & 0 \\0.5 & 0.87 & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$2. Multiplique la matriz de rotación por la geometría de entrada o, en el caso de una caja, multípliquela por cada uno de los puntos de esquina para hallar la nueva ubicación de la caja.
Escalado
Para escalar la geometría, necesitamos un factor de escala y un centro de escala. El factor de escala puede ser uniforme por igual en las direcciones x,y,z, o puede ser único para cada dimensión.
Para escalar un punto, se puede usar la siguiente ecuación:
$$P’ = ScaleFactor(S) * P$$
O bien:
$$P’.x = Sx * P.x$$
$$P’.y = Sy * P.y$$
$$P’.z = Sz * P.z$$
Este es el formato de la matriz de escalado, teniendo en cuenta que el centro del escalado es el punto de origen universal (0,0,0).
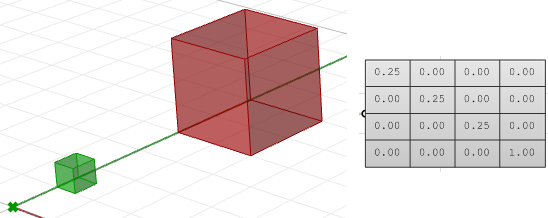
$$\begin{bmatrix}\color{red}{Scale-x} & 0 & 0 & 0 \\0 & \color{red}{Scale-y} & 0 & 0 \\0 & 0 & \color{red}{Scale-z} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Por ejemplo, si quisiéramos escalar una caja 0.25 unidades en relación con el origen universal, la matriz de escalado quedaría así:
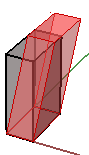
Sesgado
El sesgado en tres dimensiones se mide a lo largo de un par de ejes en relación con el tercero. Por ejemplo, el sesgado en el eje z no va a cambiar la geometría a lo largo de ese eje, sino que altera los valores en x e y. Estos son algunos ejemplos de matrices de sesgado:
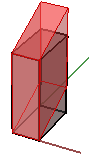
1. Sesgado en x y z, manteniendo fija la coordenada y:
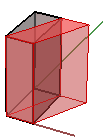$$\begin{bmatrix}1.0 &\color{red}{0.5} & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 &\color{red}{0.5} & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
2. Sesgado en y y z, manteniendo fija la coordenada x:
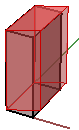$$\begin{bmatrix}1.0 & \color{red}{0.5} & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
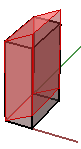$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & \color{red}{0.5} & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
3. Sesgado en x e y, manteniendo fija la coordenada z:
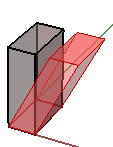$$\begin{bmatrix}1.0 & 0.0 & \color{red}{0.5} & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & \color{red}{0.5} & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
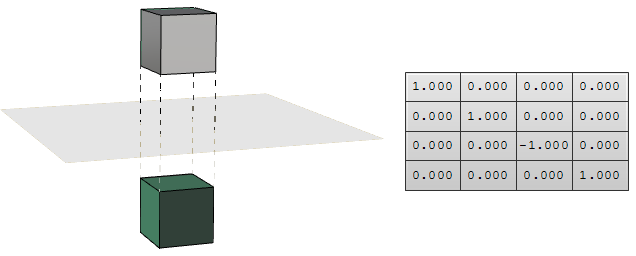
Reflejo o espejo
El reflejo o espejo crea un reflejo de un objeto a través de una línea o un plano. Los objetos 2D se reflejan a través de una línea, mientras que los objetos 3D se reflejan en un plano. Tenga en cuenta que la transformación de reflejo cambia la dirección normal de las caras de la geometría.
Proyección plana
Intuitivamente, el punto de proyección de un punto 3D dado $$P(x,y,z)$$ sobre el plano xy universal es igual a $$P_{xy} (x,y,0)$$ estableciendo el valor z en cero. De forma similar, la proyección de un punto P en el plano xz es $$P_{xz}(x,0,z)$$. Al proyectar sobre el plano, $$P_{xz} = (0,y,z)$$. Estas proyecciones se denominan proyecciones ortogonales.
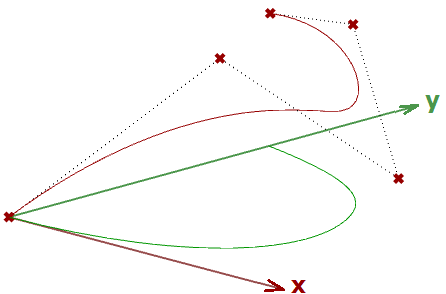
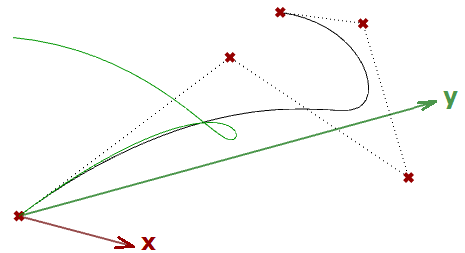
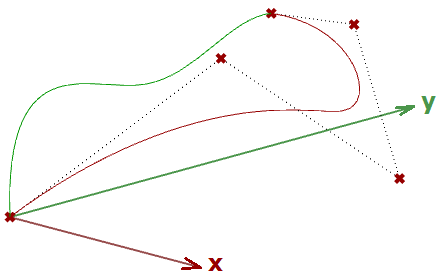
Si tenemos una curva como entrada y aplicamos la transformación de proyección plana, obtenemos una curva proyectada sobre ese plano. A continuación se muestra un ejemplo de una curva proyectada sobre el plano xy con el formato de matriz.
Nota: las curvas NURBS (que se explican en el siguiente capítulo) utilizan puntos de control para definir las curvas. La proyección de una curva pasa por la proyección de sus puntos de control.
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & \color{red}{0.0} & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & \color{red}{0.0} & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix} \color{red}{0.0} & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
Descargar archivos de muestra
Descargue este archivo , que contiene todos los archivos de ejemplo de Grasshopper y de código de esta guía.
Próximos pasos
Ahora que tiene más conocimientos sobre matrices y transformaciones, eche un vistazo a la guía Curvas y superficies paramétricas para aprender más sobre la estructura detallada de las curvas y superficies NURBS.
