Imagine que va todos los días de la semana desde su casa hasta su trabajo. Sale a las 8:00 de la mañana y llega a las 9:00. Cada momento entre las 8:00 y las 9:00, se encuentra en un punto del camino. Si traza su ubicación cada minuto durante su viaje, puede definir la trayectoria entre su casa y el trabajo conectando los 60 puntos trazados. Suponiendo que viaja exactamente a la misma velocidad todos los días, a las 8:00 estaría en su casa (ubicación de inicio), a las 9:00 estaría en el trabajo (ubicación final) y a las 8:40 estaría en la ubicación exacta de la trayectoria que corresponde al punto 40 del trazado. ¡Felicidades, acaba de definir su primera curva paramétrica! Ha utilizado el tiempo como parámetro para definir su trayectoria, y por tanto, se puede decir que la curva de trayectoria es una curva paramétrica. El intervalo de tiempo que pasa desde el inicio hasta el final (8 a 9) se denomina dominio de curva o intervalo.
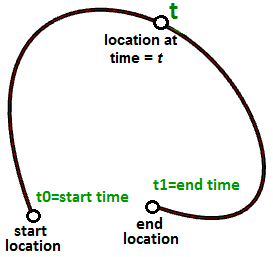
En general, podemos describir la ubicación
$$x$$,
$$y$$ y
$$z$$ de una curva paramétrica en términos de un parámetro
$$t$$ de la siguiente manera:
$$x = x(t)$$
$$y = y(t)$$
$$z = z(t)$$
Donde:
$$t$$ es un intervalo de números reales
Vimos anteriormente que la ecuación paramétrica de una línea en términos del parámetro $$t$$ se define así:
$$x = x’ + t * a$$
$$y = y’ + t * b$$
$$z = z’ + t * c$$
Donde:
$$x$$, $$y$$ y $$z$$ son funciones de t donde t representa un intervalo de números reales. $$x’$$, $$y’$$ y $$z’$$ son las coordenadas de un punto del segmento de línea. $$a$$, $$b$$, and $$c$$ definen la pendiente de la línea, de modo que el vector $$\mathbf{\vec v} <a, b, c>$$ es paralelo a la línea.
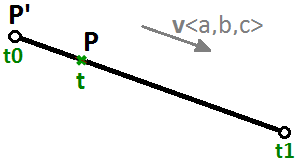
Por lo tanto, podemos escribir la ecuación paramétrica de un segmento de línea usando un parámetro $$t$$ que oscila entre dos valores numéricos reales $$t0$$, $$t1$$ y un vector unitario $$\mathbf{\vec v}$$ que está en la dirección de la línea de la siguiente manera:
$$P = P’ + t * \mathbf{\vec v}$$Otro ejemplo es un círculo. La ecuación paramétrica del círculo en el plano xy con un centro en el origen (0,0) y un parámetro de ángulo $$t$$ oscilando entre $$0$$ y $$2π$$ radianes es:
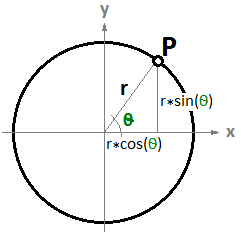
$$x = r \dot cos(t)$$
$$y = r \dot sin(t)$$
Podemos obtener la ecuación general de un círculo desde la paramétrica de la siguiente manera:
$$ x/r = cos(t)$$
$$y/r = sin(t)$$
Y puesto que:
$$cos(t)^2 + sin(t)^2 = 1$$ (Pythagorean identity)
Entonces:
$$(x/r)^2 + (y/r)^2 = 1$$ , or
$$x^2 + y^2 = r^2$$
3.1 Curvas paramétricas
Parámetro de curva
Un parámetro de una curva representa la dirección de un punto en esa curva. Como se ha mencionado anteriormente, una curva paramétrica es como una trayectoria recorrida entre dos puntos en una determinada cantidad de tiempo, desplazándose a una velocidad fija o variable. Si el desplazamiento tarda una cantidad de tiempo $$T$$, entonces el parámetro t representa un tiempo dentro de $$T$$ que se traduce en una ubicación (punto) en la curva.
Si se tiene una trayectoria recta (segmento de recta) entre los dos puntos $$A$$ y $$B$$, y $$\mathbf{\vec v}$$ fuera un vector desde $$A$$ hasta $$B$$ ( $$\mathbf{\vec v}} = B - A$$), entonces puede utilizar la ecuación de la línea paramétrica para encontrar todos los puntos $$M$$ entre $$A$$ y $$B$$ de la siguiente manera:
$$M = A + t*(B-A)$$
Donde:
$$t$$ es un valor entre 0 y 1.
El intervalo de los valores t, de 0 a 1 en este caso, se conoce como dominio de curva o intervalo. Si t es un valor fuera del dominio (menos de 0 o más de 1), entonces el punto resultante $$M$$ estará fuera de la curva lineal $$\overline{AB}$$.
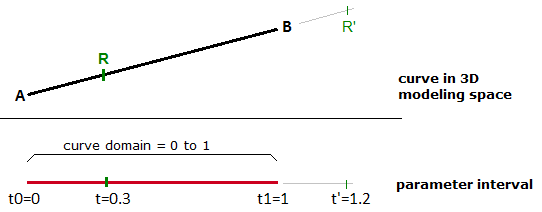
El mismo principio se aplica a cualquier curva paramétrica. Cualquier punto de la curva se puede calcular utilizando el parámetro t dentro del intervalo o dominio de valores que definen los límites de la curva. El parámetro de inicio del dominio se suele denominar $$t0$$ y el final del dominio $$t1$$.
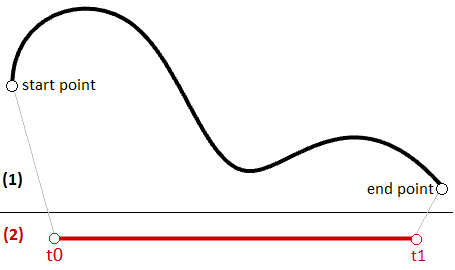
Dominio de curva o intervalo
Un dominio de curva o intervalo es el rango de parámetros que se traduce en un punto dentro de esa curva. El dominio generalmente se describe con dos números reales que definen los límites del dominio expresados en la forma (mínimo a máximo) o (mínimo, máximo). Los límites del dominio pueden ser dos valores cualesquiera que pueden estar relacionados o no con la longitud real de la curva. En un dominio creciente, el parámetro de dominio mínimo calcula el punto inicial de la curva y el dominio máximo calcula el punto final de la curva.
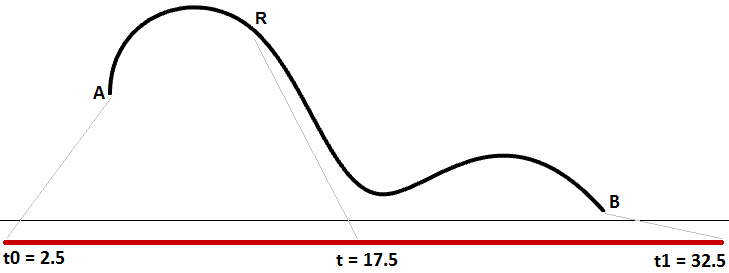
El cambio de un dominio de curva se conoce como el proceso de reparametrizar la curva. Por ejemplo, es muy común cambiar el dominio de (0 a 1). La reparametrización de una curva no afecta a la forma de la curva 3D. Como cuando se recorre un camino corriendo o caminando, cambia el tiempo que se tarda, pero no cambia la forma del camino.
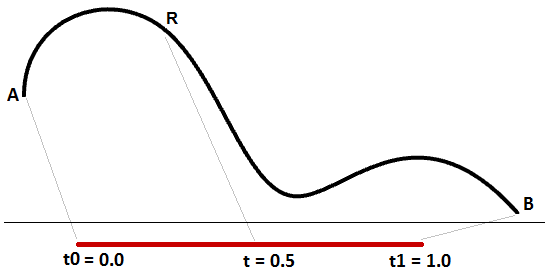
Un dominio creciente significa que el valor mínimo del dominio apunta al inicio de la curva. Los dominios suelen aumentar, pero no siempre.
Cálculo de curvas
Hemos aprendido que un intervalo de curva es el rango de todos los valores de los parámetros suelen ser puntos dentro de la curva 3D. Sin embargo, no hay garantía de que el cálculo en el medio del dominio, por ejemplo, resulte en un punto que se encuentre en el medio de la curva, como en la figura (29).
La parametrización uniforme de una curva es como recorrer un camino a una velocidad constante. Una línea de grado 1 entre dos puntos es un ejemplo en el que los intervalos o parámetros iguales se traducen en intervalos iguales de longitud de arco en la línea. Se trata de un caso especial en el que los intervalos iguales de parámetros se traduzcan en intervalos iguales en la curva 3D.
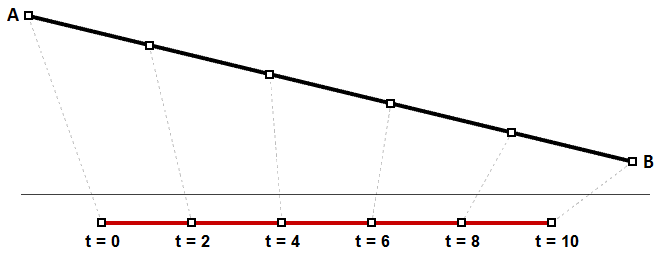
Sin embargo, es más probable que la velocidad disminuya o aumente a lo largo del recorrido. Por ejemplo, si tarda 30 minutos en recorrer una carretera, es poco probable que esté exactamente a la mitad en el minuto 15. La figura (30) muestra un caso típico en el que los intervalos de parámetros iguales se traducen en una longitud variable en la curva 3D.
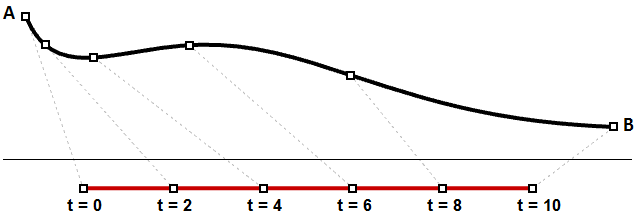
Es posible que tenga que calcular puntos en una curva 3D que se encuentren en un porcentaje definido de la longitud de la curva. Por ejemplo, puede que tenga que dividir la curva en longitudes iguales. Normalmente, los modeladores 3D proporcionan herramientas para calcular curvas en relación con la longitud del arco.
Vector tangente a una curva
Una tangente a una curva en cualquier parámetro (o punto de una curva) es el vector que toca la curva en ese punto, pero no se cruza. La pendiente del vector tangente es igual a la pendiente de la curva en el mismo punto. El siguiente ejemplo calcula la tangente a una curva en dos parámetros diferentes.
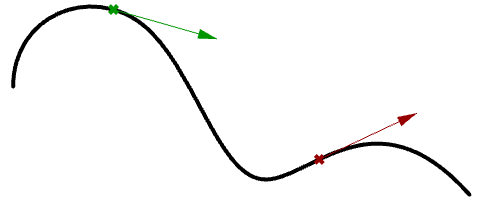
Curvas polinomiales cúbicas
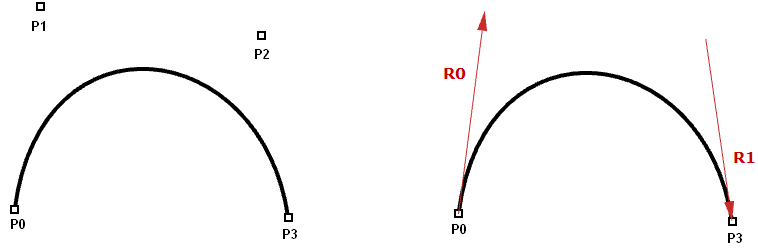
Las curvas Hermite y Bézier son dos ejemplos de curvas polinomiales cúbicas determinadas por cuatro parámetros. Una curva Hermite viene determinada por sus dos puntos finales y dos vectores de dirección tangentes a estos puntos, mientras que una curva Bézier está definida por cuatro puntos. A pesar de ser diferentes matemáticamente, comparten características y limitaciones similares.
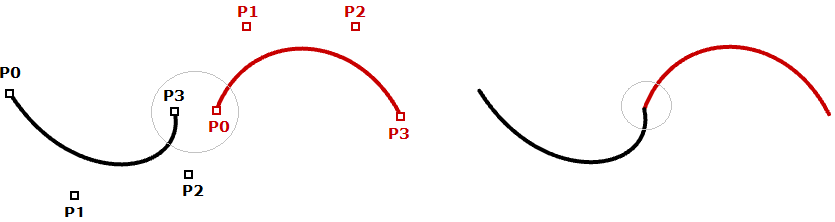
En la mayoría de casos, las curvas están compuestas por varios segmentos. Esto requiere lo que se denomina curva cúbica segmentada. Aquí se muestra una figura de una curva Bézier que utiliza 7 puntos para crear una curva de tres segmentos. Nótese que, aunque la última curva esta unida, no se ve suave o continua.
Aunque las curvas Hermite emplean la misma cantidad de parámetros que las Bézier (4 para definir la curva), tenemos información adicional de la tangente que se puede compartir con el siguiente tramo para crear una curva de apariencia más suave con menos información, como se muestra a continuación.
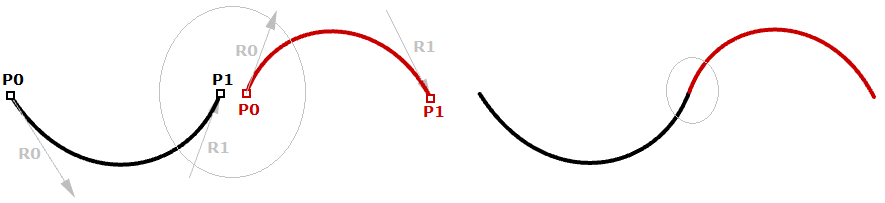
Para obtener curvas más suaves y continuas, hay una representación de curvas muy potente denominada Non Uniform Rational B-Spline (NURBS). Los segmentos comparten más puntos de control para conseguir más suavidad con menos información.
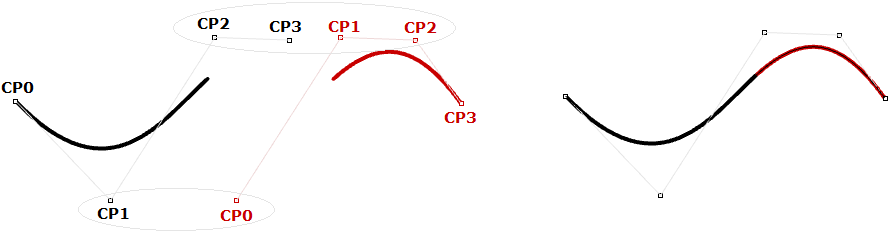
Las curvas y superficies NURBS son la principal representación matemática que utiliza Rhino para representar la geometría. Las características y los componentes de las curvas NURBS se tratarán en detalle a lo largo de este capítulo.
Cálculo de curvas de Bézier cúbicas
Con el nombre su inventor, Paul De Casteljau, el algoritmo de De Casteljau calcula las curvas Bézier utilizando un método iterativo. Los pasos del algoritmo se pueden resumir de la siguiente manera:
Entrada:
Cuatro puntos $$A$$, $$B$$, $$C$$, $$D$$ definen una curva $$t$$, es cualquier parámetro dentro del dominio de la curva
Resultado:
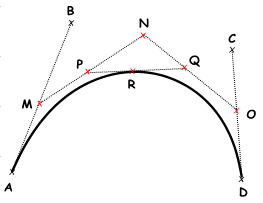
Point $$R$$ en la curva que está en el parámetro $$t$$.
Solución:
- Halle el punto
$$M$$ en el parámetro
$$t$$ de la línea
$$\overline{AB}$$.
2.Halle el punto $$N$$ en el parámetro $$t$$ de la línea $$\overline{BC}$$.
3.Halle el punto $$O$$ en el parámetro $$t$$ de la línea $$overline{CD}$$.
4.Halle el punto $$P$$ en el parámetro $$t$$ de la línea $$overline{MN}$$.
5.Halle el punto $$Q$$ en el parámetro $$t$$ de la línea $$overline{NO}$$.
6.Halle el punto $$R$$ en el parámetro $$t$$ de la línea $$overline{PQ}$$.
3.2 Curvas NURBS
NURBS es un método exacto de representación matemática de curvas muy intuitivo a la hora de editar. Es fácil representar curvas de forma libre utilizando NURBS y la estructura de control hace que su edición sea fácil y predecible.
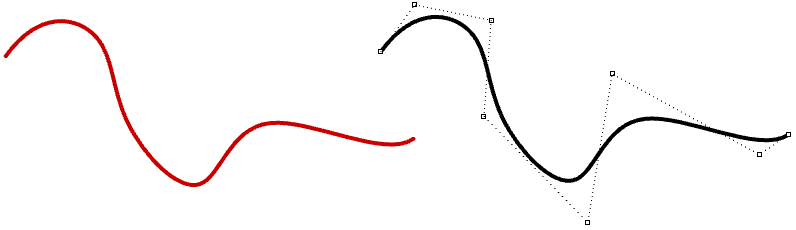
Existen multitud de libros y referencias para quien le interese investigar más en profundidad sobre las NURBS. Sin embargo, es necesario tener conocimientos básicos de las NURBS para poder utilizar un modelador NURBS de un modo eficaz. Una curva NURBS viene definida por cuatro atributos principales: grado, puntos de control, nodos y reglas de cálculo.
Grado
El grado de la curva es un número entero positivo. Rhino permite trabajar con cualquier grado empezando po el 1. Los grados 1, 2, 3 y 5 son los más útiles, mientras que los grados 4 y los superiores a 5 no se usan mucho en el mundo real. A continuación se muestran algunos ejemplos de curvas y su grado:
| Las líneas y las polilíneas son curvas NURBS de grado 1. |  |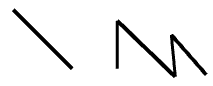
| Los círculos y las elipses son curvas NURBS de grado 2. |  |
| Las curvas de forma libre normalmente se representan como curvas NURBS de grado 3 o 5. |  |
Puntos de control
Los puntos de control de una curva NURBS son una lista de puntos de grado 1 como mínimo. La manera más común de modificar la forma de una curva NURBS es moviendo sus puntos de control.
El número de puntos de control que afectan a cada segmento de una curva NURBS viene definido por el grado de la curva. Por ejemplo, cada segmento de una curva de grado 1 solo se ve afectado por los dos puntos de control finales. En una curva de grado 2, cada segmento se ve afectado por tres puntos de control, y así sucesivamente.
| Los puntos de control de las curvas de grado 1 pasan por todos los puntos de control de la curva. En una curva NURBS de grado 1, dos puntos de control (grado +1) definen cada segmento. Con cinco puntos de control, la curva tiene cuatro segmentos. |  |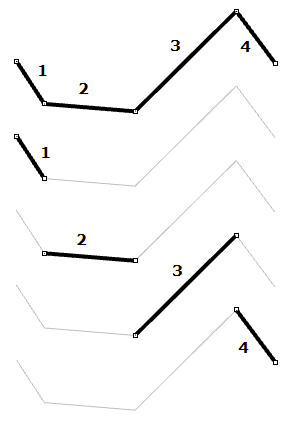
| Los círculos y las elipses son ejemplos de curvas de grado 2. En una curva NURBS de grado 2, tres puntos de control (grado +1) definen cada segmento. Con cinco puntos de control, la curva tiene tres segmentos. |  |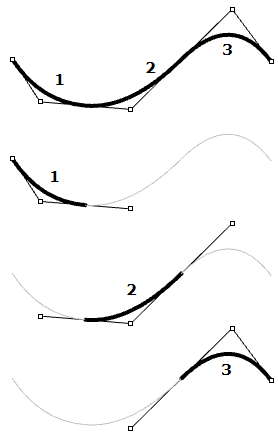
| Los puntos de control de las curvas de grado 3 no suelen tocar la curva, excepto en los puntos finales de las curvas abiertas. En una curva NURBS de grado 3, cuatro puntos de control (grado +1) definen cada segmento. Con cinco puntos de control, la curva tiene dos segmentos. |  |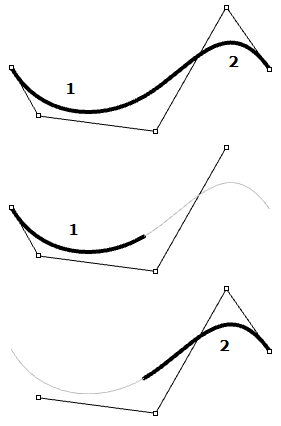
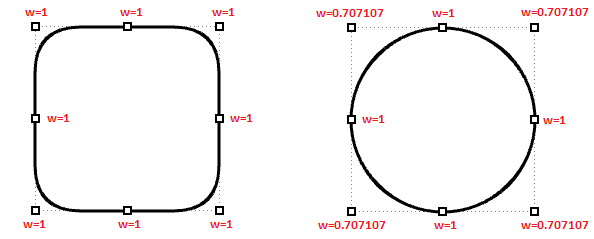
Peso de los puntos de control
Los puntos de control llevan asociado un número denominado peso. Con algunas excepciones, los pesos son números positivos. Cuando todos los puntos de control tienen el mismo peso, normalmente 1, la curva se denomina no racional. Los pesos son como la cantidad de gravedad que tiene cada punto de control. Cuanto mayor sea el peso relativo de un punto de control, más se acercará la curva a ese punto de control.
Cabe señalar que es mejor no cambiar los pesos de las curvas. Cambiar los pesos no suele dar el resultado deseado y puede presentar problemas de cálculo en operaciones como las intersecciones. El único buen motivo para usar curvas racionales es representar curvas que no se pueden dibujar de otra manera, como los círculos y las elipses.
Nodos
Cada curva NURBS tiene una lista de números asociados a ella denominada lista de nodos (o vectores nodales). Los nodos son algo más difíciles de comprender y manejar. Si utiliza un modelador 3D, no tendrá que definir manualmente los nodos para cada curva que cree.
Los nodos son valores de parámetros
Los nodos son una lista no decreciente de valores de parámetros que se encuentran dentro del dominio de la curva. En Rhino, hay más nodos de grado 1 que puntos de control. Es decir, el número de nodos es igual al número de puntos de control más el grado de la curva menos 1:
|nodos| = |curvas| + grado -1
Normalmente, para curvas no periódicas, los nodos de primer grado son iguales al dominio mínimo y los nodos de último grado son iguales al dominio máximo.
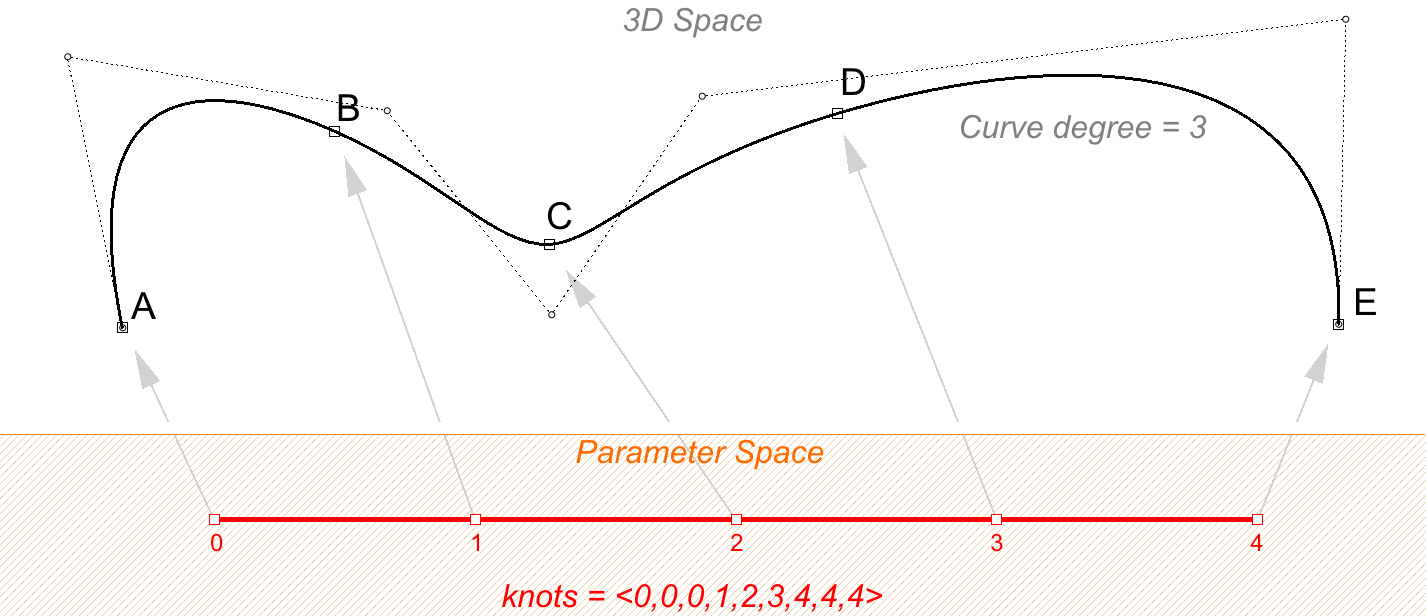
Por ejemplo, los nodos de una curva NURBS de grado 3 abierta con 7 puntos de control y un dominio entre 0 y 4 serían así: <0, 0, 0, 1, 2, 3, 4,4, 4>.
Escalar una lista de nodos no afecta a la curva 3D. Si cambia el dominio de la curva en el ejemplo anterior de “0 a 4” a “0 a 1”, la lista de nodos se escala, pero la curva 3D no cambia.
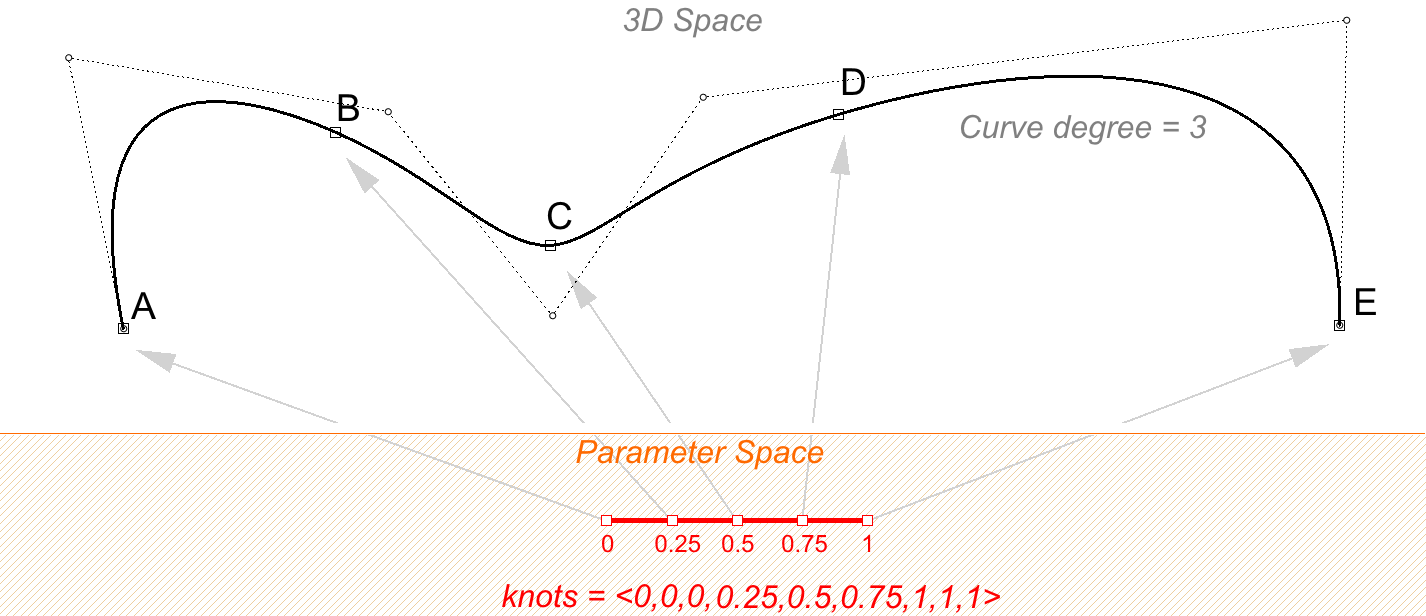
Un nodo cuyo valor aparece solo una vez se denomina nodo simple. Los nodos interiores suelen ser simples, como en los dos ejemplos anteriores.
Multiplicidad de nodos
La multiplicidad de un nodo es el número de veces que se encuentra en la lista de nodos. La multiplicidad de un nodo no puede ser mayor que el grado de la curva. La multiplicidad nodal se utiliza para controlar la continuidad en el correspondiente punto de la curva.
Nodos de multiplicidad total
Un nodo de multiplicidad total tiene una multiplicidad igual al grado de la curva. En un nodo de multiplicidad total existe un punto de control que le corresponde, y la curva pasa por este punto.
Por ejemplo, las curvas ancladas tienen nodos de multiplicidad total en los finales de la curva. Esta es la razón por la que los puntos de control finales coinciden con los puntos finales de la curva. Los nodos interiores de multiplicidad total generan un punto de torsión en el punto correspondiente de la curva.
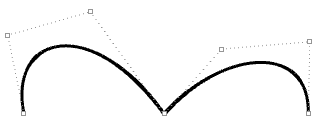
Por ejemplo, las dos curvas siguientes son de grado 3 y tienen el mismo número y ubicación de puntos de control. Sin embargo, tienen diferentes nodos y su forma también es diferente. La multiplicidad total obliga a la curva a pasar por el punto de control asociado.
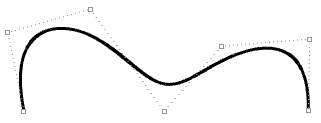
Aquí hay dos curvas que tienen el mismo grado, y el mismo número y ubicación de puntos de control, y sin embargo tienen diferentes nodos, lo que resulta en diferentes formas de curva:
| Degree = 3 Número de puntos de control = 7 knots = <0,0,0,1,2,3,4,4,4> = 9 knots Dominio (0 a 4) |
 |
| Degree = 3 Número de puntos de control = 7 knots = <0,0,0,1,1,1,4,4,4> = 9 knots Dominio (0 a 4) Nota: un nodo de multiplicidad total en el medio crea un punto de torsión y la curva se ve obligada a pasar por el punto de control asociado. |
 |
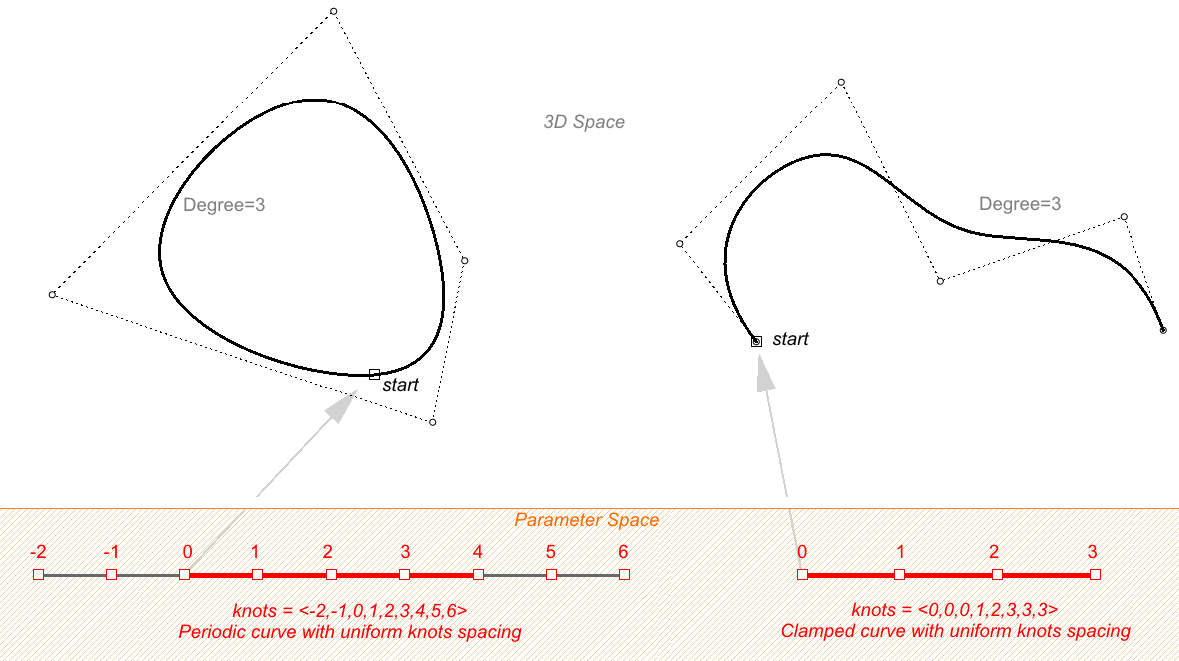
Nodos uniformes
Una lista uniforme de nodos satisface la siguiente condición.
Los nodos comienzan con un nodo de multiplicidad total, seguido de nodos simples y terminan con otro nodo de multiplicidad total. Los valores son crecientes a intervalos regulares. Esto es típico de las curvas cerradas o abiertas. Las curvas periódicas funcionan de manera diferente, como veremos más adelante.
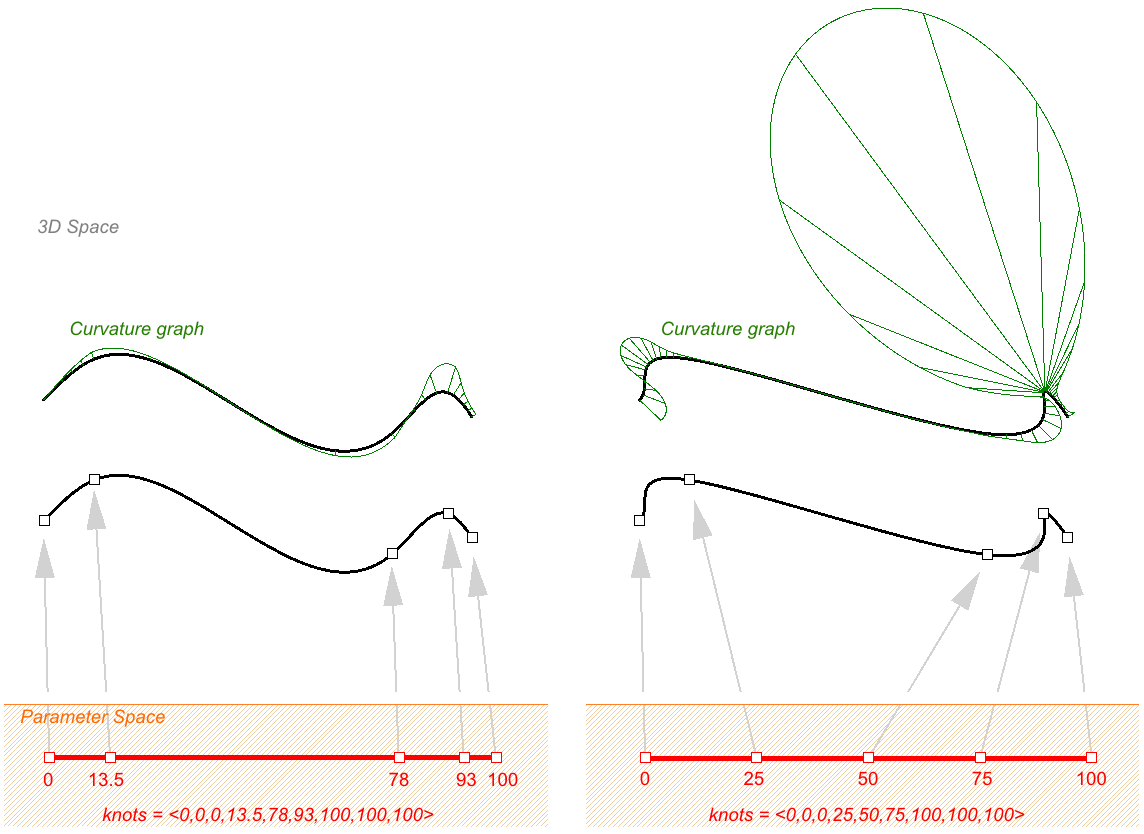
Nodos no uniformes
Las curvas NURBS pueden tener un espaciado no uniforme entre los nodos. Esto puede ayudar a controlar la curvatura a lo largo de la curva para crear curvas más suaves. Vea el siguiente ejemplo de interpolación a través de puntos usando una lista de nodos no uniformes a la izquierda y uniformes a la derecha. En general, si el espaciado de nodos de una curva NURBS es proporcional al espaciado entre los puntos de control, entonces la curva es más suave.
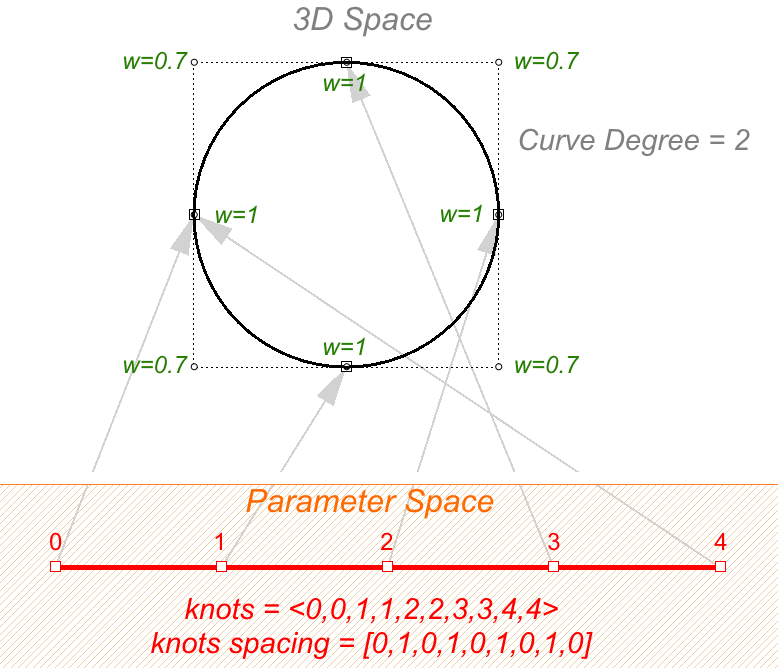
Un ejemplo de curva no uniforme y racional es un círculo NURBS. La siguiente curva es de grado 2 con 9 puntos de control y 10 nodos. El dominio es 0-4 y el espaciado se alterna entre 0 y 1. knots = <0,0,1,1,2,2,3,3,4,4> — (full multiplicity in the interior knots) espaciado entre nodos = [0,1,0,1,0,1,0,1,0] — (no uniforme)
Regla de cálculo
La regla de cálculo utiliza una fórmula matemática que coge un número dentro del dominio de la curva y asigna un punto. La fórmula tiene en cuenta el grado, los puntos de control y los nodos.
Empleando esta fórmula, las funciones de curva especializadas pueden tomar un parámetro de curva y producir el punto correspondiente en esa curva. Un parámetro es un número que se encuentra dentro del dominio de la curva. Los dominios son normalmente crecientes y consisten en dos números: el parámetro mínimo del dominio $$t(0)$$ suele ser el punto inicial de la curva y el parámetro máximo $$t(1)$$ suele ser el final de la curva.
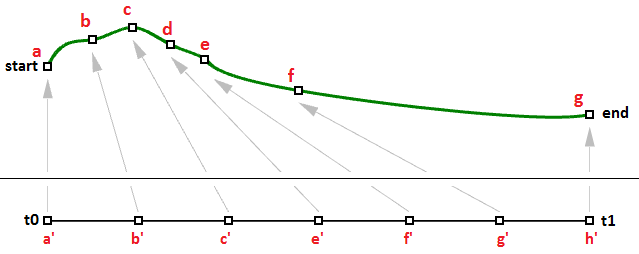
Características de las curvas NURBS
Para generar una curva NURBS, necesitará la siguiente información:
- Dimensión, normalmente 3
- Grado, (algunas veces se utiliza el orden, que es igual a grado+1)
- Puntos de control (lista de puntos)
- Peso de puntos de control (lista de números)
- Nodos (lista de números)
Cuando se crea una curva, es necesario al menos definir el grado y la ubicación de los puntos de control. El resto de la información necesaria para crear curvas NURBS se puede generar automáticamente. Si se selecciona un punto final para que coincida con el punto inicial, normalmente se crea una curva cerrada suave periódica. La siguiente tabla muestra ejemplos de curvas abiertas y cerradas:
| Curva abierta de grado 1. La curva pasa por todos los puntos de control. |
 |
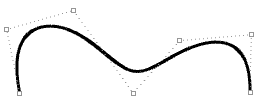
| Curva abierta de grado 3. Ambos finales de la curva coinciden con los puntos de control finales. |
 |
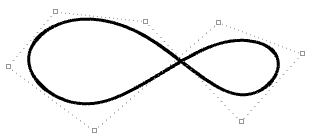
| Curva periódica cerrada de grado 3. La costura de la curva no pasa por ningún punto de control. |
 |
| Mover los puntos de control de una curva periódica no repercute en la suavidad de la curva. |  |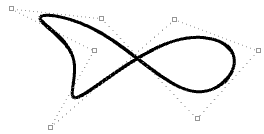
| Las puntos de torsión se crean cuando la curva se ve obligada a pasar por algunos puntos de control. |  |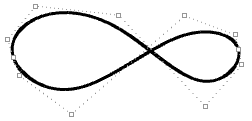
| Mover los puntos de control de una curva no periódica no garantiza una continuidad uniforme de la curva, pero permite un mayor control sobre el resultado. |  |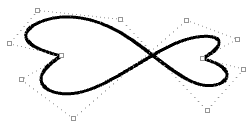
Curvas NURBS ancladas vs. periódicas
Los puntos finales de las curvas cerradas ancladas coinciden con los puntos de control finales. Las curvas periódicas son curvas cerradas suaves. La mejor manera de comprender las diferencias entre las dos es comparando los puntos de control y los nodos.
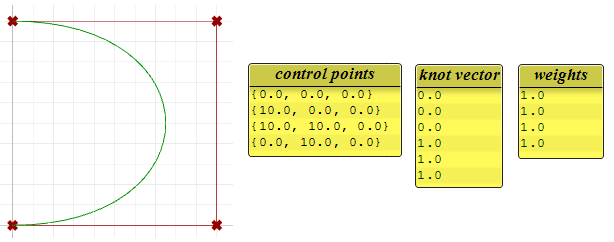
El siguiente ejemplo es una curva NURBS no racional, anclada y abierta. Esta curva tiene cuatro puntos de control, nodos uniformes de multiplicidad total en los nodos inicial y final y los pesos de todos los puntos de control iguales a 1.
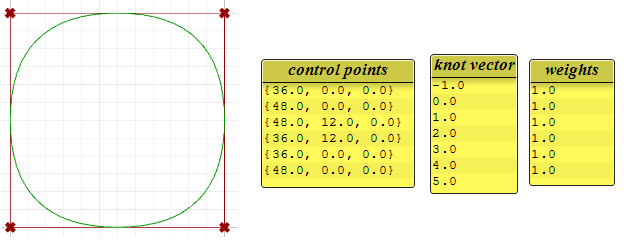
La siguiente curva circular es un ejemplo de una curva NURBS periódica cerrada de grado 3. También es no racional porque todos los pesos son iguales. Tenga en cuenta que las curvas periódicas necesitan más puntos de control con pocas superposiciones. Los nodos también son simples.
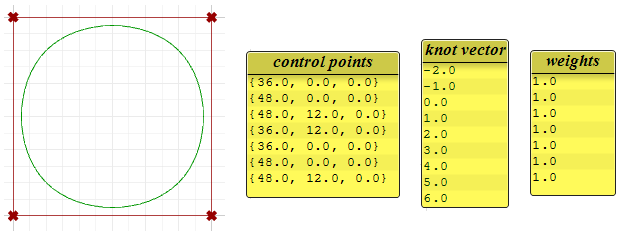
Observe que la curva periódica convirtió los cuatro puntos de entrada en siete puntos de control (grado+4), mientras que la curva anclada solo utilizó los cuatro puntos de control. Los nodos de la curva periódica utilizan solo nodos simples, mientras que los nodos de inicio y final de la curva anclada tienen multiplicidad total, lo que obliga a la curva a pasar por los puntos de control de inicio y final.
Si establecemos el grado de los ejemplos anteriores a 2 en lugar de 3, los nodos se vuelven más pequeños y el número de puntos de control de las curvas periódicas cambia.
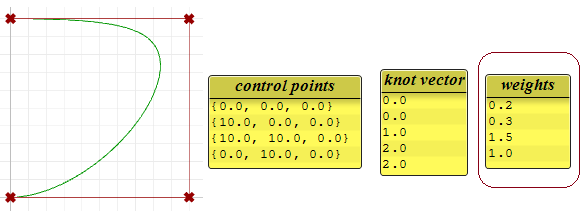
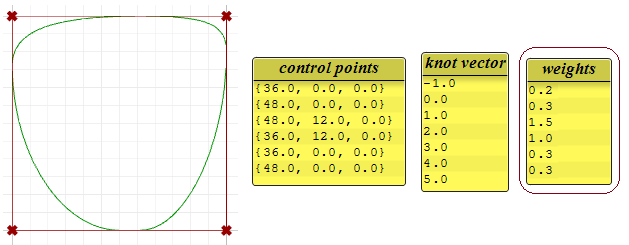
Pesos
Los pesos de los puntos de control de una curva NURBS uniforme se establecen en 1, pero este número puede variar en curvas NURBS racionales. El siguiente ejemplo muestra el efecto de variar los pesos de los puntos de control.
Cálculo de curvas NURBS
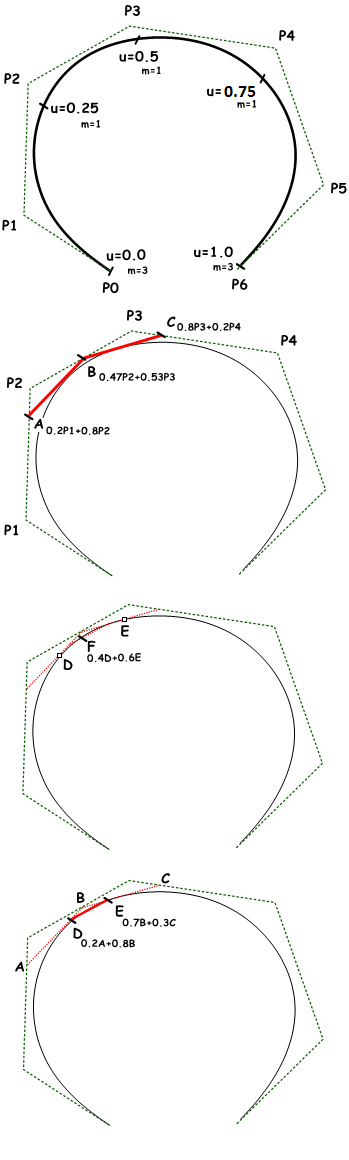
El algoritmo de De Boor, que lleva el nombre de su inventor, Carl de Boor, es una generalización del algoritmo de De Casteljau para curvas de Bézier. Es estable numéricamente, y su uso está muy extendido para calcular puntos en curvas NURBS dentro de las aplicaciones 3D. A continuación se muestra un ejemplo para calcular un punto en una curva NURBS de grado 3 utilizando el algoritmo de De Boor.
Entrada:
Siete puntos de control
$$P0$$ a
$$P6$$
Nodos:
$$u_0 = 0.0$$
$$u_1 = 0.0$$
$$u_2 = 0.0$$
$$u_3= 0.25$$
$$u_4 = 0.5$$
$$u_5 = 0.75$$
$$u_6 = 1.0$$
$$u_7 = 1.0$$
$$u_8 = 1.0$$
Resultado:
Punto de la curva que está en $$u=0.4$$
Solución:
1. Calcule los coeficientes para la primera iteración:
$$A_c = ((u – u_1)/(u_{1+3} – u_1) = 0.8$$
$$B_c = (u – u_2)/(u_{2+3} – u_2) = 0.53$$
$$C_c = (u – u_3)/(u_{3+3} – u_3) = 0.2$$
2. Calcule los puntos usando datos de los coeficientes:
$$A = 0.2P_1 + 0.8P_2$$
$$B = 0.47 P_2 + 0.53 P_3$$
$$C = 0.8 P_3 + 0.2 P_4$$
3. Calcule los coeficientes para la segunda iteración:
$$D_c = (u – u_2) / (u_{2+3-1} – u_2) = 0.8$$
$$E_c = (u – u_3) / (u_{3+3-1} – u_3) = 0.3$$
4. Calcule los puntos usando datos de los coeficientes:
$$D = 0.2A+ 0.8B$$
$$E = 0.7B + 0.3C$$
5. Calcule el último coeficiente:
$$Fc = (u – u_3)/ (u_{3+3-2} – u_3) = 0.6$$
Encuentre el punto en la curva en el parámetro $$u=0.4$$:
$$F= 0.4D + 0.6E$$
3.3 Continuidad geométrica de curva
La continuidad es un concepto importante en el modelado 3‑D. La continuidad es importante para lograr la suavidad visual y para obtener una luz y un flujo de aire suaves. La siguiente tabla muestra varias continuidades y sus definiciones:
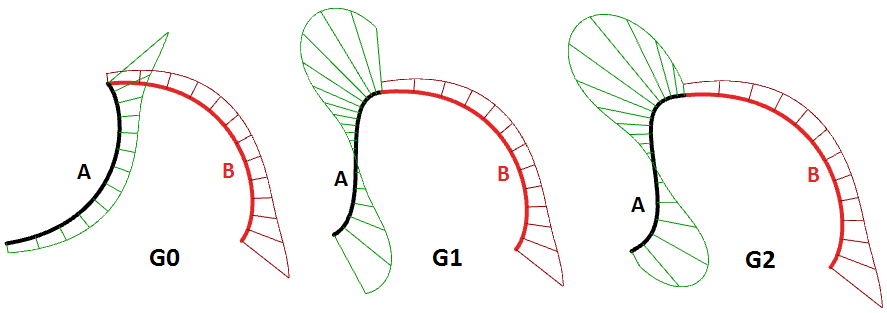
| G0| (Continuidad de posición) | Dos segmentos de curva unidos |
| G1| (Continuidad de tangencia) | La dirección de la tangente en el punto de unión es la misma para ambos segmentos de la curva. |
| G2| (Continuidad de curvatura) | Tanto las curvaturas como las tangentes coinciden para ambos segmentos de curva en el punto final común |
| GN|……. | Las curvas coinciden con un orden superior|
3.4 Curvatura de curva
La curvatura es un concepto ampliamente utilizado en el modelado de superficies y curvas 3‑D. La curvatura se define como el cambio en la inclinación de la tangente de una curva por unidad de longitud de arco. Para un círculo o esfera, es la inversa del radio y es constante en todo el dominio.
En cualquier punto en una curva del plano, la línea que mejor se aproxima a la curva que atraviesa este punto es la línea tangente. También podemos encontrar el círculo más aproximado que atraviese este punto y sea tangente a la curva. La inversa del radio de este círculo es la curvatura de la curva en este punto.
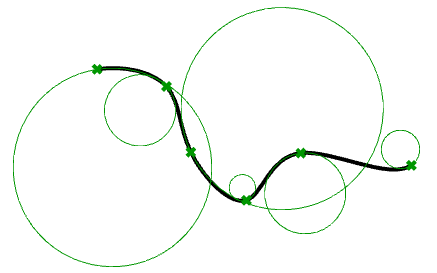
El círculo más aproximado puede estar situado a la izquierda de la curva o a la derecha. Si tenemos esto en cuenta, podemos establecer una convención, como dar un símbolo positivo a la curvatura si el círculo se encuentra a la izquierda y negativo si el círculo se encuentra a la derecha de la curva. Esto se denomina curvatura señalada. Los valores de curvatura de las curvas unidas indican la continuidad entre estas curvas.
3.5 Superficies paramétricas
Parámetros de superficie
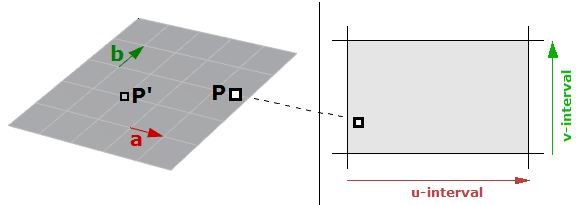
Una superficie paramétrica es una función de dos parámetros independientes (generalmente $$u$$, $$v$$) sobre algún dominio bidimensional. Tomemos como ejemplo un plano. Si tenemos un punto $$P$$ en el plano y dos vectores no paralelos en el plano, $$\vec a$$ y $$\vec b$$, entonces podemos definir una ecuación paramétrica del plano en términos de los dos parámetros $$u$$ y $$v$$ de la siguiente manera:
$$P = P’ + u * \mathbf{\vec a} + v * \mathbf{\vec b}$$Donde:
$$P’$$: es un punto conocido en el plano
$$\mathbf{\vec a}$$: es el primer vector en el plano
$$\mathbf{\vec b}$$: es el primer vector en el plano
$$u$$: es el primer parámetro
$$v$$: es el primer parámetro
Otro ejemplo es la esfera. La ecuación cartesiana de una esfera centrada en el origen con radio $$R$$ es
$$x^2 + y^2 + z^2 = R^2$$Eso significa que para cada punto hay tres variables ( $$x$$, $$y$$, $$z$$), lo cual no es útil para una representación paramétrica que requiere solo dos variables. Sin embargo, en el sistema de coordenadas esféricas, cada punto utiliza los tres valores:
$$r$$: distancia radial entre el punto y el origen
$$θ$$: ángulo desde el eje x en el plano xy
$$ø$$: ángulo desde el eje z y el punto
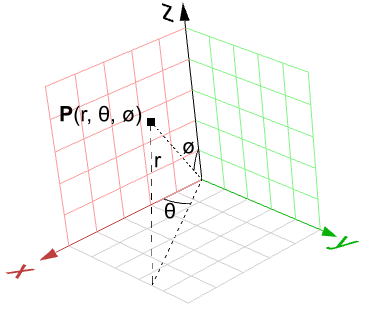
Se puede obtener una conversión de puntos de coordenadas esféricas a cartesianas de la siguiente manera:
$$x = r * sin(ø) * cos(θ)$$
$$y = r * sin(ø) * sin(θ)$$
$$z = r * cos (ø)$$
Donde:
$$r$$ es la distancia desde el origen
$$≥ 0$$
$$θ$$ va de
$$0$$ a
$$2π$$
$$ø$$ va de
$$0$$ a
$$π$$
Puesto que $$r$$ es constante en una superficie de esfera, nos quedan solo dos variables y, por tanto, podemos usar lo indicado anteriormente para crear una representación paramétrica de una superficie de esfera:
$$u = θ$$
$$v = ø$$
De manera que:
$$x = r * sin(v) * cos(u)$$
$$y = r * sin(v) * sin(u)$$
$$z = r * cos(v)$$
Donde ( $$u$$, $$v$$) está dentro del dominio ( $$2 π$$, $$π$$).
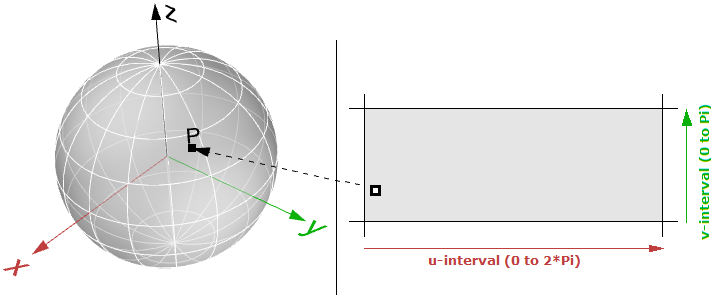
La superficie paramétrica sigue la forma general:
$$x = x(u,v)$$
$$y = y(u,v)$$
$$z = z(u,v)$$
Donde:
$$u$$ y $$v$$ son los dos parámetros dentro del dominio o región de superficie.
Dominio de superficie
Un dominio de superficie se define como el rango de parámetros ( $$u,v$$) que se traducen en un punto 3D en esa superficie. El dominio en cada dimensión ( $$u$$ o $$v$$) suele describirse como dos números reales ( $$u_{min}$$ a $$u_{max}$$) y ( $$v_{min}$$ a $$v_{max}$$)
El cambio de un dominio de superficie se conoce como reparametrizar la superficie. Un dominio creciente significa que el valor mínimo del dominio apunta al punto mínimo de la superficie. Los dominios suelen aumentar, pero no siempre.
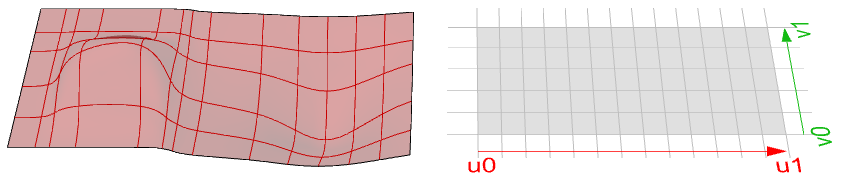
Cálculo de superficies
Calcular una superficie en un parámetro que está dentro del dominio de la superficie da como resultado un punto que está en la superficie. Tenga en cuenta que el medio del dominio ( $$u_{mid}$$, $$v_{mid}$$) puede no calcular necesariamente el punto medio de la superficie 3D. Además, el cálculo de los valores $$u-$$ y $$v-$$ que están fuera del dominio de la superficie no dará un resultado útil.
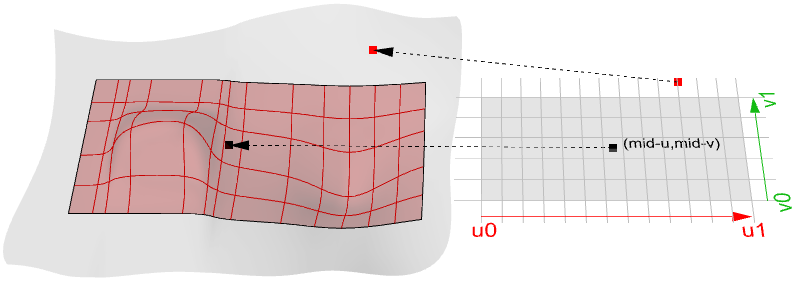
Plano tangente de una superficie
El plano tangente a una superficie en un punto dado es el plano que toca la superficie en ese punto. La dirección z del plano tangente representa la dirección normal de la superficie en ese punto.
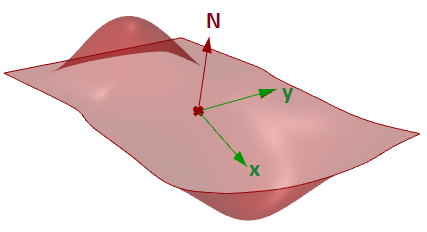
3.6 Continuidad geométrica de superficie
Muchos modelos no se pueden construir a partir de un parche de superficie. La continuidad entre los parches de superficies unidas es importante para la suavidad visual, el reflejo de la luz y el flujo de aire. La siguiente tabla muestra varias continuidades y sus definiciones:
| G0| (Continuidad de posición) | Dos superficies unidas. |
| G1| (Continuidad de tangencia) | Las tangentes correspondientes de las dos superficies a lo largo de su borde de unión son paralelas en ambas direcciones u y v. |
| G2| (Continuidad de curvatura) | Tanto las curvaturas como las tangentes coinciden para ambos superficies en el borde común. |
| GN|……. | Las superficies coinciden en un orden mayor. |
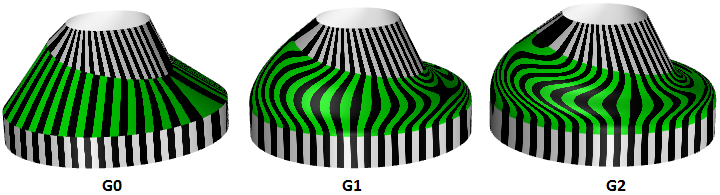
3.7 Curvatura de superficie
Para superficies, la curvatura normal es una generalización de la curvatura aplicada a las superficies. Dado un punto en la superficie y una dirección situada en el plano tangente de la superficie en ese punto, la curvatura de sección normal se calcula intersecando la superficie con el plano segmentado por el punto, la normal a la superficie en ese punto y la dirección. La curvatura de sección normal es la curvatura señalada de esta curva en el punto de interés.
Si miramos en todas las direcciones en el plano tangente a la superficie en nuestro punto y calculamos la curvatura normal en todas esas direcciones, habrá un valor máximo y un valor mínimo.
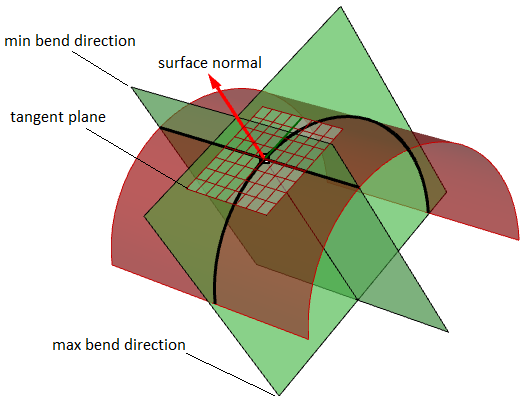
Curvaturas principales
Las curvaturas principales de una superficie en un punto son el mínimo y el máximo de las curvaturas normales en ese punto. Miden la cantidad máxima y mínima de curvatura de la superficie en ese punto. Las curvaturas principales se usan para calcular las curvaturas gaussianas y medias de la superficie.
Por ejemplo, en una superficie cilíndrica, no hay ninguna curvatura en la dirección lineal (la curvatura es igual a cero) mientras que la curvatura máxima se produce cuando se interseca con un plano paralelo a las caras de los extremos (la curvatura es igual a 1/radio). Esos dos extremos forman las curvaturas principales de esa superficie.
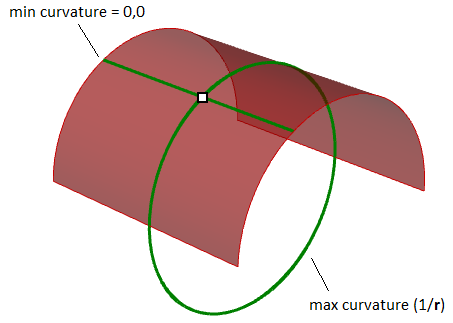
Curvatura gaussiana
La curvatura gaussiana de una superficie en un punto es el producto de las curvaturas principales en ese punto. El plano tangente de cualquier punto con curvatura gaussiana positiva toca la superficie localmente en un solo punto, mientras que el plano de cualquier punto con curvatura gaussiana negativa corta la superficie.
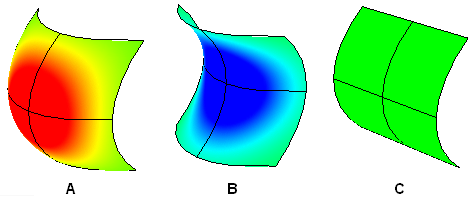
A: curvatura positiva cuando la superficie tiene forma de cuenco.
B: curvatura negativa cuando la superficie tiene forma de silla de montar.
C: curvatura cero cuando la superficie es plana en al menos una dirección (plano, cilindro).
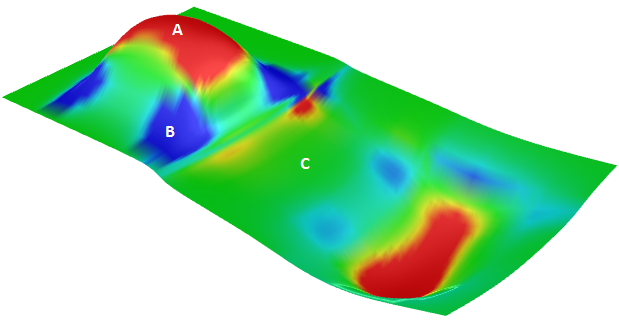
Curvatura media
La curvatura media de una superficie en un punto la mitad de las sumas de las curvaturas principales en ese punto. Cualquier punto con un curvatura media de cero tiene una curvatura gaussiana negativa o de cero.
Las superficies con una curvatura media de cero en todas partes son superficies mínimas. Los procesos físicos que pueden ser modelados por superficies mínimas incluyen la formación de capas de jabón que se extienden en objetos fijos, como bucles de estructura alámbrica. Una capa de jabón no se deforma por la presión del aire (que es igual en ambos lados) y es libre de minimizar su área. Por el contrario, una burbuja de jabón encierra una cantidad fija de aire y tiene presiones desiguales en el interior y el exterior. La curvatura media sirve para hallar áreas de cambio brusco en la curvatura de la superficie.
Las superficies con una curvatura media constante en todas partes a menudo se conocen como superficies de curvatura media constante (CMC). Las superficies CMC incluyen la formación de burbujas, tanto libres como asociadas a los objetos. Una burbuja de jabón, a diferencia de una simple capa de jabón, encierra un volumen y existe en equilibrio donde la presión ligeramente mayor dentro de la burbuja queda compensada por las fuerzas de superficie mínima de la misma burbuja.
3.8 Superficies NURBS
Las superficies NURBS son como una rejilla de curvas NURBS en dos direcciones. La forma de una superficie NURBS está definida por el número de puntos de control y el grado de la superficie en cada una de las dos direcciones (u y v). Las superficies NURBS sirven para almacenar y representar superficies de forma libre con un alto grado de precisión. Las ecuaciones matemáticas y los detalles de las superficies NURBS están fuera del alcance de este documento. Solo nos centraremos en las características que son más útiles para los diseñadores.
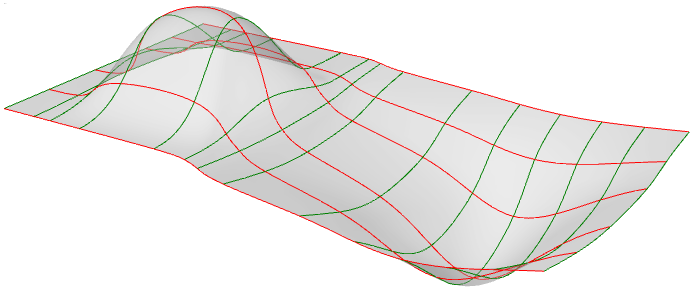
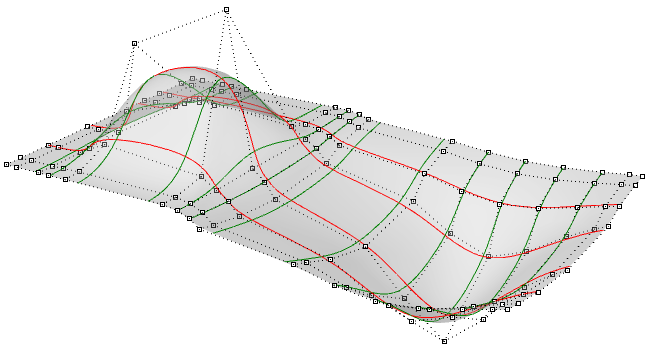
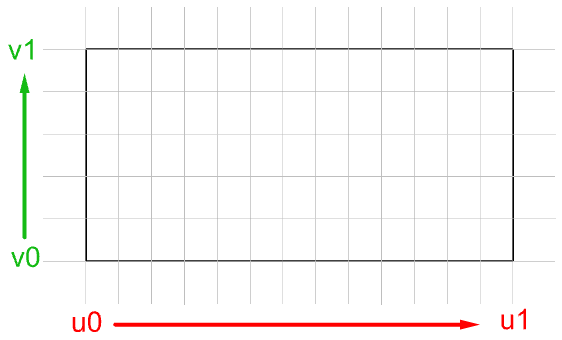
Calcular parámetros a intervalos iguales en el rectángulo de parámetros 2D no se traduce en intervalos iguales en el espacio 3D en la mayoría de los casos.
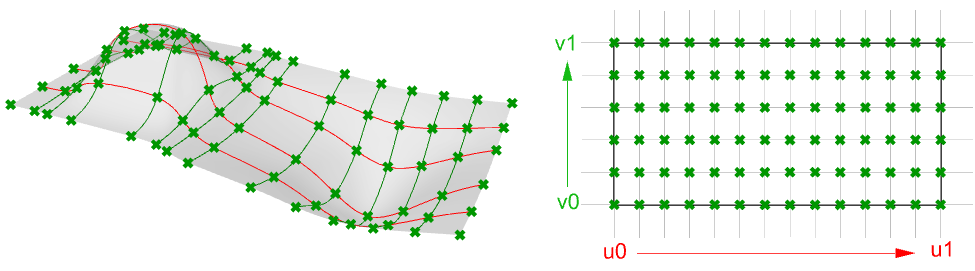
Características de las superficies NURBS
Las características de las superficies NURBS son muy similares a las de las curvas NURBS excepto en que tienen un parámetro adicional. Las superficies NURBS contienen la siguiente información:
- Dimensión, normalmente 3
- Grado en direcciones u y v: (a veces se utiliza el orden que es grado + 1)
- Puntos de control (puntos)
- Pesos de los puntos de control (números)
- Nodos (números)
Al igual que con las curvas NURBS, probablemente no necesitará conocer los detalles de cómo crear una superficie NURBS, ya que los modeladores 3D normalmente disponen de un buen conjunto de herramientas para ayudarle. Siempre se pueden reconstruir las superficies (y las curvas) a un nuevo grado y número de puntos de control. Una superficie puede ser abierta, cerrada o periódica. A continuación, se muestran algunos ejemplos de superficies:
| Superficie de grado 1 en ambas direcciones u y v. Todos los puntos de control se encuentran en la superficie. |  |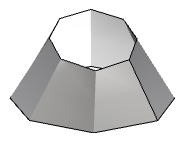
| Superficie abierta de grado 3 en la dirección u y de grado 1 en la en la dirección v. Las esquinas de la superficie coinciden con los puntos de control de las esquinas. |  |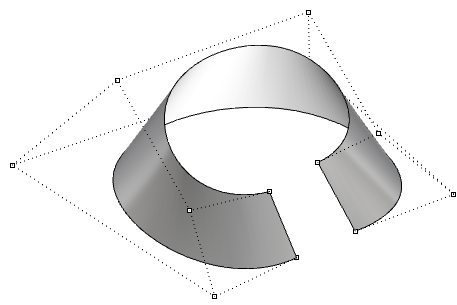
| Superficie cerrada (no periódica) de grado 3 en la dirección u y de grado 1 en la en la dirección v. Algunos puntos de control coinciden con la costura de la superficie. |  |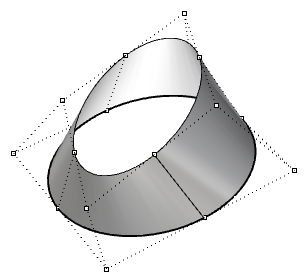
| Al mover los puntos de control de una superficie cerrada (no periódica), se crea un punto de torsión y la superficie deja de ser suave. |  |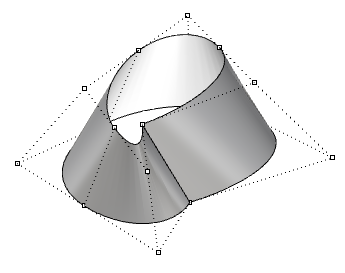
| Superficie periódica de grado 3 en la dirección u y de grado 1 en la dirección v. Los puntos de control de la superficie no coinciden con la costura de la superficie. |  |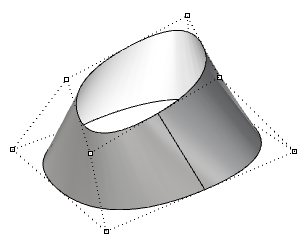
| Mover los puntos de control de una superficie periódica no repercute en su suavidad ni crea puntos de torsión. |  |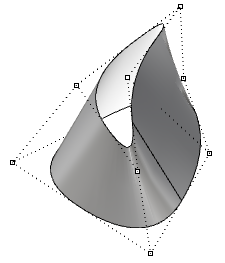
Singularidad en las superficies NURBS
Por ejemplo, si tiene un borde lineal de un plano simple y arrastra los dos puntos de control finales de un borde para que se superpongan (contraigan) en el medio, obtendrá un borde singular. Verá que las curvas isoparamétricas de la superficie convergen en el punto singular.
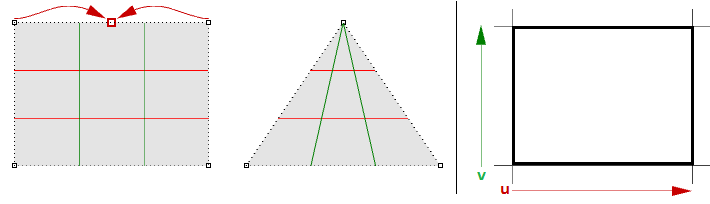
La forma triangular anterior se puede crear sin singularidad. Puede recortar una superficie con una polilínea triangular. Si examina la estructura NURBS subyacente, verá que sigue siendo una forma rectangular.
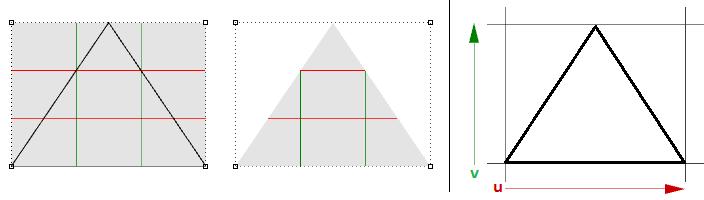
Otros ejemplos comunes de superficies difíciles de generar sin singularidad son el cono y la esfera. La parte superior de un cono y los bordes superior e inferior de una esfera se contraen en un solo punto. Tanto si hay singularidad como si no la hay, el rectángulo de parámetros mantiene una zona más o menos rectangular.
Superficies NURBS recortadas
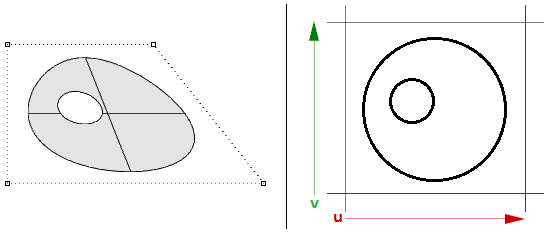
Las superficies NURBS pueden ser recortadas (trimmed) o no recortadas (untrimmed). Las superficies recortadas utilizan una superficie NURBS subyacente y curvas cerradas para recortar parte de esa superficie. Cada superficie tiene una curva cerrada que define el borde exterior (bucle exterior) y puede tener curvas interiores cerradas que no se intersecan para definir agujeros (bucles interiores). Una superficie con un bucle exterior igual que el de su superficie NURBS subyacente y que no tiene agujeros se denomina superficie no recortada.
3.9 Polisuperficies
Una polisuperficie está formada por dos o más superficies unidas (posiblemente recortadas). Cada superficie tiene su propia estructura, parametrización y direcciones de isocurva que no tienen por qué coincidir. Las polisuperficies se representan mediante lo que se denomina boundary representation (representación de bordes), abreviado * brep*. La estructura brep describe superficies, bordes y vértices con datos de los recortes y relaciones entre las diferentes partes. Las superficies recortadas también se representan mediante la estructura de datos brep.
La brep es una estructura de datos que describe cada cara en términos de su superficie subyacente, bordes 3D que la rodean, vértices, recortes 2D del espacio de parámetros y relaciones con las caras adyacentes. Los objetos brep también se denominan sólidos cuando son cerrados (herméticos).
Un ejemplo de polisuperficie es una caja simple compuesta por seis superficies no recortadas unidas entre sí.
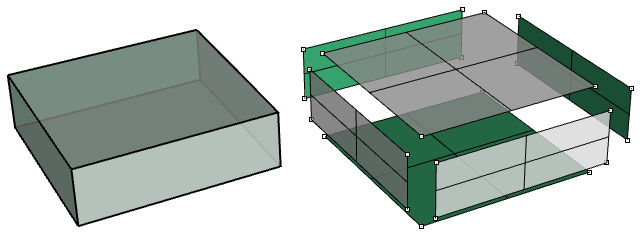
Se puede crear la misma caja utilizando superficies recortadas, como la del siguiente ejemplo.
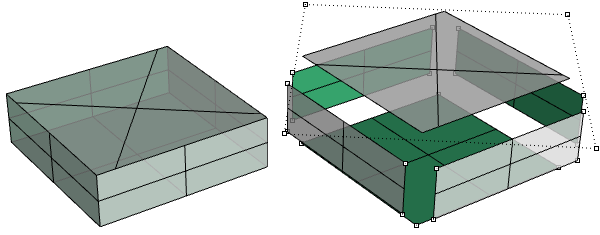
En el siguiente ejemplo, las caras superior e inferior del cilindro son caras recortadas de superficies planas.
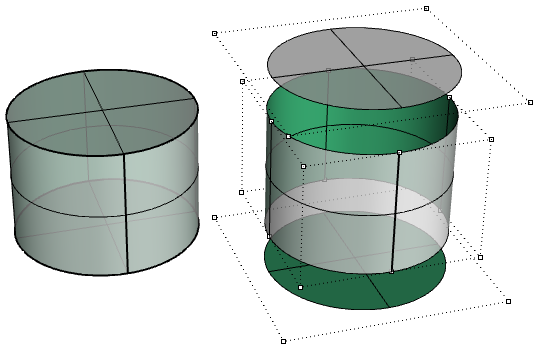La Figura 72 muestra los puntos de control de las superficies subyacentes.
Hemos visto que la edición de curvas NURBS y superficies no recortadas es intuitiva y se puede realizar de forma interactiva moviendo los puntos de control. Sin embargo, la edición de superficies y polisuperficies recortadas no es tan fácil. Lo que resulta complicado es mantener los bordes unidos de las diferentes caras dentro de la tolerancia deseada. Las caras adyacentes que comparten bordes comunes se pueden recortar y no suelen tener una estructura NURBS coincidente, por lo que modificar el objeto deformando ese borde común podría generar una abertura.
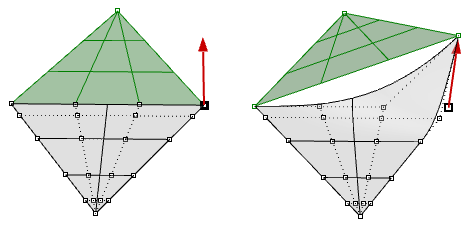
Otra dificultad es que normalmente hay menos control sobre el resultado, sobre todo cuando se modifica la geometría recortada.
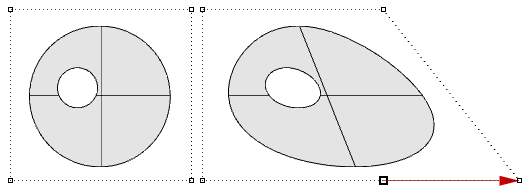
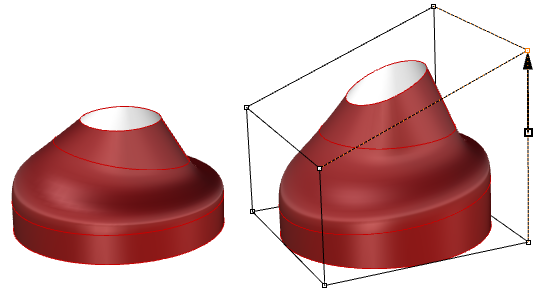
Las superficies recortadas se describen en el espacio de parámetros utilizando la superficie subyacente no recortada combinada con las curvas de corte 2D que pasan a ser bordes 3D dentro de la superficie 3D.
3.10 Tutoriales
Los siguientes tutoriales utilizan los conceptos aprendidos en este capítulo. Utilizan Rhinoceros 5 y Grasshopper 0.9.
3.10.1 Continuidad entre curvas
Analiza la continuidad entre dos curvas de entrada. La continuidad supone que las curvas se encuentran al final de la primera curva y al inicio de la segunda curva.
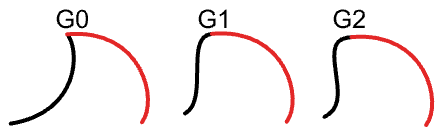
Entrada:
Dos curvas de entrada.
Parámetros:
Calcule los siguientes parámetros para conocer la continuidad entre dos curvas:
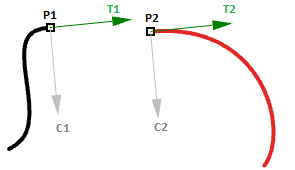
- El punto final de la primera curva ( $$P1$$)
- El punto inicial de la segunda curva ( $$P2$$)
- La tangente al final de la primera curva y al inicio de la segunda curva ( $$T1$$ y $$T2$$).
- La curvatura al final de la primera curva y al inicio de la segunda curva ( $$C1$$ y $$C2$$).
Solución:
1. Reparametrice las curvas de entrada. Lo hacemos para saber que el inicio de la curva se calcula en
$$t=0$$ y el final en
$$t=1$$.
2. Extraiga los puntos final e inicial de las dos curvas y compruebe si coinciden. Si es así, las dos curvas son tienen al menos continuidad
$$G0$$.
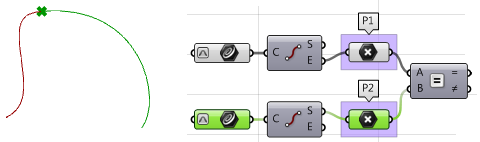
3. Calcule las tangentes.
4. Compare las tangentes utilizando el producto escalar. Asegúrese de unificar los vectores. Si las curvas son paralelas, entonces tenemos al menos continuidad
$$G1$$.
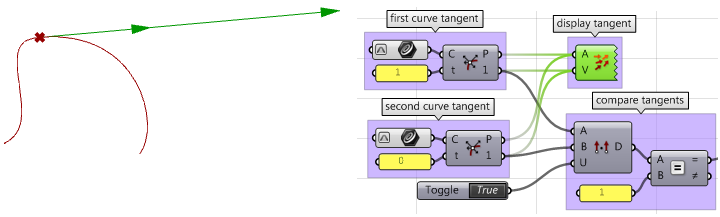
5. Calcule los vectores de curvatura.
6. Compare los vectores de curvatura y, si coinciden, las dos curvas tienen continuidad
$$G2$$.
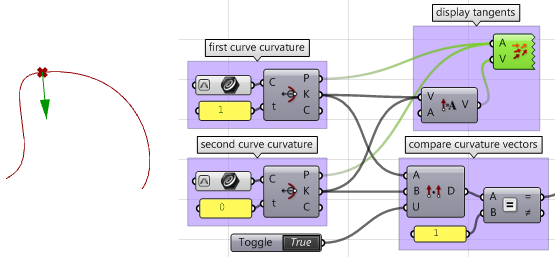
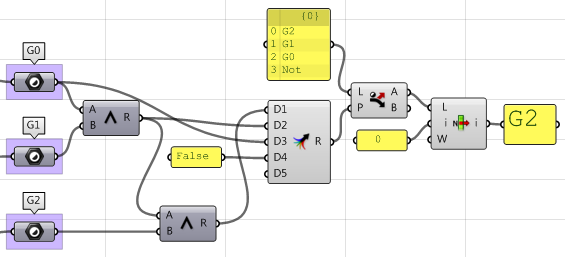
7. Cree una lógica que filtre los tres resultados (G1, G2 y G3) y seleccione la continuidad máxima.
Uso del componente VBScript de Grasshopper:
Private Sub RunScript(ByVal c1 As Curve, ByVal c2 As Curve, ByRef A As Object)
'declare variables
Dim continuity As New String("")
Dim t1, t2 As Double
Dim v_c1, v_c2, c_c1, c_c2 As Vector3d
'extract start and end points
Dim end_c1 = c1.PointAtEnd
Dim start_c2 = c2.PointAtStart
'check G0 continuity
If end_c1.DistanceTo(start_c2) = 0 Then
continuity = "G0"
End If
'check G1 continuity
If continuity = "G0" Then
'calculate tangents
v_c1 = c1.TangentAtEnd
v_c2 = c2.TangentAtStart
'unitize tangent vectors
v_c1.Unitize
v_c2.Unitize
'compare tangents
If v_c1 * v_c2 = 1.0 Then
continuity = "G1"
End If
End If
'check G2 continuity
If continuity = "G1" Then
'extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max
t2 = c2.Domain.Min
'calculate curvature
c_c1 = c1.CurvatureAt(t1)
c_c2 = c2.CurvatureAt(t2)
'unitize curvature vectors
c_c1.Unitize
c_c2.Unitize
'compare vectors
If c_c1 * c_c2 = 1.0 Then
continuity = "G2"
End If
End If
'Assign output
A = continuity
End Sub
Uso del componente Python de Grasshopper:
#decclare variables
continuity = ""
#extract start and end points
end_c1 = c1.PointAtEnd
start_c2 = c2.PointAtStart
#check G0 continuity
if end_c1.DistanceTo(start_c2) == 0:
continuity = "G0"
#check G1 continuity
if continuity == "G0":
#calculate tangents
v_c1 = c1.TangentAtEnd
v_c2 = c2.TangentAtStart
#unitize tangent vectors
v_c1.Unitize()
v_c2.Unitize()
#compare tangents
dot = v_c1 * v_c2
if dot == 1.0:
continuity = "G1"
else:
print("Failed G1")
print(dot)
#check G2 continuity
if continuity == "G1":
#extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max
t2 = c2.Domain.Min
#calculate curvature
c_c1 = c1.CurvatureAt(t1)
c_c2 = c2.CurvatureAt(t2)
#unitize curvature vectors
c_c1.Unitize()
c_c2.Unitize()
#compare vectors
dot = c_c1 * c_c2
if dot == 1.0:
continuity = "G2"
else:
print("Failed G2")
print(dot)
#assign output
A = continuity
Uso del componente C# de Grasshopper:
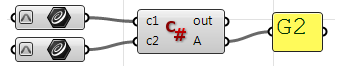
Private Sub RunScript(ByVal c1 As Curve, ByVal c2 As Curve, ByRef A As Object)
//declare variables
string continuity = ("");
double t1, t2;
Vector3d v_c1, v_c2, c_c1, c_c2;
//extract start and end points
Point3d end_c1 = c1.PointAtEnd;
Point3d start_c2 = c2.PointAtStart;
//check G0 continuity
if( end_c1.DistanceTo(start_c2) == 0){
continuity = "G0";
}
//check G1 continuity
if( continuity == "G0")
{
//calculate tangents
v_c1 = c1.TangentAtEnd;
v_c2 = c2.TangentAtStart;
//unitize tangent vectors
v_c1.Unitize();
v_c2.Unitize();
//compare tangents
if( v_c1 * v_c2 == 1.0 ){
continuity = "G1";
}
}
//check G2 continuity
if( continuity == "G1" )
{
//extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max;
t2 = c2.Domain.Min;
//calculate curvature
c_c1 = c1.CurvatureAt(t1);
c_c2 = c2.CurvatureAt(t2);
//unitize curvature vectors
c_c1.Unitize();
c_c2.Unitize();
//compare vectors
if( c_c1 * c_c2 == 1.0 ){
continuity = "G2";
}
}
//assign output
A = continuity;
End Sub
3.10.2 Superficies con singularidad
Extraiga puntos singulares en una esfera y un cono.
Entrada:
Una esfera y un cono.
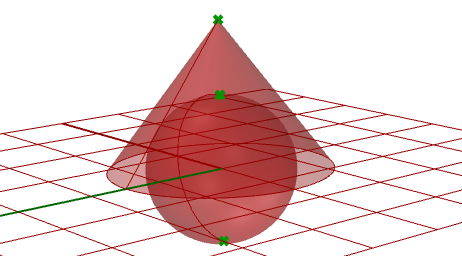
Parámetros:
La singularidad se puede detectar analizando los recortes del espacio de parámetros 2D que tienen bordes correspondientes no válidos o de longitud cero. Esos recortes deberían ser singulares.
Solución:
- Compruebe todos los recortes de la entrada.
- Compruebe si algún recorte tiene un borde no válido y márquelo como recorte singular.
- Extraiga las ubicaciones de los puntos en el espacio 3D.
Uso del componente VB de Grasshopper:
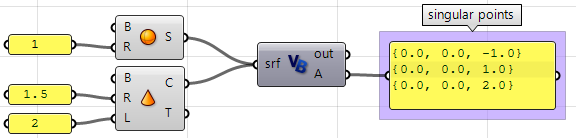
Private Sub RunScript(ByVal srf As Brep, ByRef A As Object)
'Declare a new list of points
Dim singular_points As New List( Of Point3d)
'Examine all trims in the input
For Each trim As BrepTrim In srf.Trims
'Null edge of a trim indicates a singularity
If trim.Edge Is Nothing Then
'Find the 2D parameter space point of the start or end of the trim
Dim pt2d = New Point2d(trim.PointAtStart)
'Evaluate trim end point on the object surface
Dim pt3d = trim.Face.PointAt(pt2d.x, pt2d.y)
'Add 3D point to the list of singular points
singular_points.Add(pt3d)
End If
Next
'Asign output
A = singular_points
End Sub
Uso del componente Python de Grasshopper:
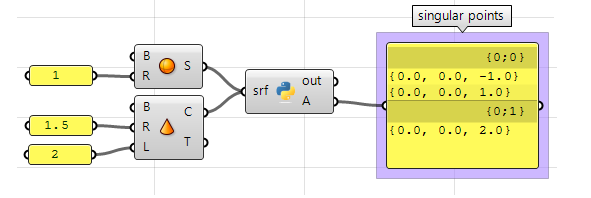
#Declare a new list of points
singular_points = []
#Examine all trims in the input brep
for trim in srf.Trims:
#Null edge of a trim indicates a singularity
if trim.Edge == None:
#Find the 2D parameter space point at trim start or end
pt2d = trim.PointAtStart
#Evaluate trim end point on the object surface
pt3d = trim.Face.PointAt(pt2d.X, pt2d.Y)
#Add 3D point to the list of singular points
singular_points.append(pt3d)
#Asign output
A = singular_points
Uso del componente C# de Grasshopper:
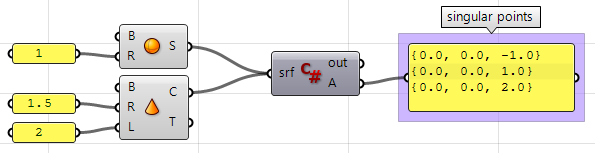
private void RunScript(Brep srf, ref object A)
{
//Decalre a new list of points
List < Point3d > singular_points = new List<Point3d>();
//Examine all trims in the input
foreach( BrepTrim trim in srf.Trims)
{
//Null edge of a trim indicates a singularity
if( trim.Edge == null)
{
//Find the 2D parameter space point of the start or end of the trim
Point2d pt2d = new Point2d(trim.PointAtStart);
//Evaluate trim end point on the object surface
Point3d pt3d = trim.Face.PointAt(pt2d.X, pt2d.Y);
//Add 3D point to the list of singular points
singular_points.Add(pt3d);
}
}
//Asign output
A = singular_points
}
Descargar archivos de muestra
Descargue el archivo math-samplesandtutorials.zip , que contiene todos los archivos de ejemplo de Grasshopper y de código de esta guía.
Próximos pasos
Si desea investigar más, consulte la guía Referencias para obtener más información sobre la estructura detallada de las curvas y superficies NURBS.
