Un vector representa un parámetro, como la velocidad o la fuerza, que tiene dirección y longitud. Los vectores en sistemas de coordenadas 3D se representan con un conjunto ordenado de tres números reales de la forma:
$$\mathbf{\vec v} = <a_1, a_2, a_3>$$1.1 Representación vectorial
En este documento, las letras minúsculas en negrita representarán los vectores. Los componentes de un vector también se representarán entre paréntesis angulares. Las letras mayúsculas representarán los puntos. Las coordenadas de los puntos siempre se representarán entre paréntesis.
Utilizando un sistema de coordenadas y cualquier conjunto de puntos de anclaje en ese sistema, podemos representar o visualizar estos vectores dibujándolos como el segmento de una línea. Dibujamos también la punta de una flecha para representar la dirección de los vectores.
Por ejemplo, si tenemos un vector que tiene una dirección paralela al eje x de un sistema de coordenadas dado y una magnitud de 5 unidades, podemos escribir el vector de la siguiente manera:
$$\mathbf{\vec v} = <5, 0, 0>$$Para representar ese vector, necesitamos un punto de anclaje en el sistema de coordenadas. Por ejemplo, todas las flechas de la siguiente figura son representaciones iguales del mismo vector a pesar de que están ancladas en diferentes ubicaciones.
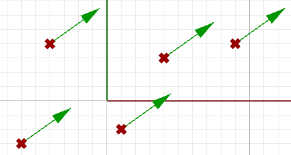
Entonces, ¿cómo definimos los puntos finales de un segmento de línea que representa un vector dado? Definamos un punto de anclaje (A) de modo que:
$$A = (1, 2, 3)$$Y un vector:
$$\mathbf{\vec v} = <5, 6, 7>$$El punto extremo $$(B)$$ del vector se calcula sumando los componentes correspondientes del punto de anclaje y el vector $$\vec v$$:
$$B = A + \mathbf{\vec v}$$
$$B = (1+5, 2+6, 3+7) $$
$$B = (6, 8, 10)$$
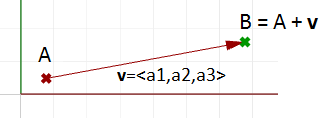
Vector de posición
Existe una representación especial de vectores que utiliza el $$\text{punto de origen} (0,0,0)$$ como punto de anclaje del vector. El vector de posición $$\mathbf{\vec v} = <a_1,a_2,a_3>$$ se representa con un segmento de línea entre dos puntos, el origen y B, de modo que:
$$\text{Punto de origen} = (0,0,0)$$
$$B = (a_1,a_2,a_3)$$
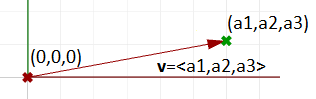
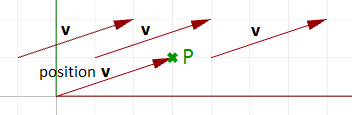
Vectores y puntos
Es importante no confundir vectores con puntos. Son conceptos muy diferentes. Los vectores, como mencionamos, representan una cantidad que tiene dirección y longitud, mientras que los puntos indican una ubicación. Por ejemplo, la dirección norte es un vector, mientras que el polo norte es una ubicación (punto). Si tenemos un vector y un punto que tienen los mismos componentes, como por ejemplo:
$$\mathbf{\vec v} = <3,1,0>$$
$$P = (3,1,0)$$
Podemos dibujar el vector y el punto de la siguiente manera:
Longitud vectorial
Como se ha mencionado anteriormente, los vectores tienen longitud. Usaremos $$\vert a \vert$$ para representar la longitud de un vector dado $$ a $$. Por ejemplo:
$$\mathbf{\vec a} = <4, 3, 0>$$
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5$$
En general, la longitud de un vector $$\mathbf{\vec a} <a_1,a_2,a_3>$$ se calcula de la siguiente manera:
$$\vert \mathbf{\vec a} \vert = \sqrt{(a_1)^2 + (a_2)^2 + (a_3)^2} $$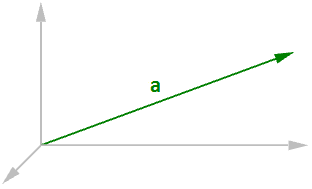
Vector unitario
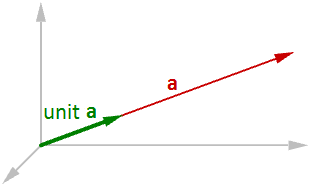
Un vector unitario es un vector con una longitud igual a una unidad. Los vectores unitarios se utilizan comúnmente para comparar las direcciones de los vectores.
Para calcular un vector unitario, necesitamos encontrar la longitud del vector dado y luego dividir los componentes del vector por la longitud. Por ejemplo:
$$\mathbf{\vec a} = <4, 3, 0>$$
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5 \text{ unidades de longitud}$$
Si
$$\mathbf{\vec b} = \text{vector unitario}$$ de
$$a$$, entonces:
$$\mathbf{\vec b} = <4/5, 3/5, 0/5>$$
$$\mathbf{\vec b} = <0.8, 0.6, 0>$$
$$\vert \mathbf{\vec b} \vert = \sqrt{0.8^2 + 0.6^2 + 0^2}$$
$$\vert \mathbf{\vec b} \vert = \sqrt{0.64 + 0.36 + 0}$$
$$\vert \mathbf{\vec b} \vert = \sqrt{(1)} = 1 \text{ unidad de longitud}$$
En general:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$El vector unitario de $$\mathbf{\vec a} = <a_1/\vert \mathbf{\vec a} \vert , a_2/\vert \mathbf{\vec a} \vert , a_3/\vert \mathbf{\vec a} \vert >$$
1.2 Operaciones vectoriales
Operación escalar de vectores
La operación escalar de vectores implica multiplicar un vector por un número. Por ejemplo:
$$\mathbf{\vec a} = <4, 3, 0>$$
$$2* \mathbf{\vec a} = <24, 23, 2*0> $$
$$2*\mathbf{\vec a} = <8, 6, 0>$$
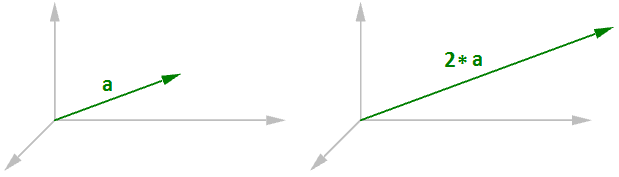
En general, dado el vector $$\mathbf{\vec a} = <a_1, a_2, a_3>$$ y un número real $$t$$
$$t*\mathbf{\vec a} = < t* a_1, t* a_2, t* a_3 >$$Suma de vectores
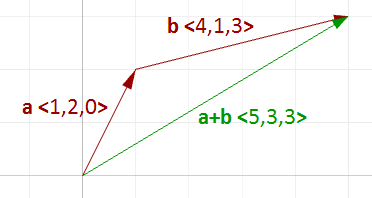
La suma de vectores toma dos vectores y se obtiene un tercer vector. Sumamos vectores añadiendo sus componentes.
Por ejemplo, si tenemos dos vectores:
$$\mathbf{\vec a} = <1, 2, 0> $$
$$\mathbf{\vec b} = <4, 1, 3> $$
$$\mathbf{\vec a}+\mathbf{\vec b} = <1+4, 2+1, 0+3>$$
$$\mathbf{\vec a}+\mathbf{\vec b} = <5, 3, 3>$$
En general, la suma de vectores de los dos vectores a y b se calcula de la siguiente manera:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a}+\mathbf{\vec b} = <a_1+b_1, a_2+b_2, a_3+b_3>$$
La suma de vectores es útil para hallar la dirección media de dos o más vectores. En estos casos, solemos usar vectores de la misma longitud. Este es un ejemplo que muestra la diferencia entre emplear vectores de iguales o de diferentes longitudes en la resultante de la suma de dichos vectores:
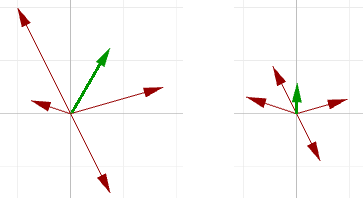
Es probable que los vectores de entrada no tengan la misma longitud. Para encontrar la dirección media, tiene que utilizar el vector unitario de los vectores de entrada. Como se ha mencionado anteriormente, el vector unitario es un vector de que tiene una longitud igual a 1.
Resta de vectores
La resta de vectores toma dos vectores y se obtiene un tercer vector. Restamos dos vectores restando los componentes correspondientes. Por ejemplo, si tenemos dos vectores $$\mathbf{\vec a}$$ and $$\mathbf{\vec b}$$ y restamos $$\mathbf{\vec b}$$ de $$\mathbf{\vec a}$$, entonces:
$$\mathbf{\vec a} = <1, 2, 0> $$
$$\mathbf{\vec b} = <4, 1, 4> $$
$$\mathbf{\vec a}-\mathbf{\vec b} = <1-4, 2-1, 0-4>$$
$$\mathbf{\vec a}-\mathbf{\vec b} = <-3, 1, -4> = \mathbf{\mathbf{\vec b}a}$$
Si restamos $$\mathbf{\vec b}$$ de $$\mathbf{\vec a}$$, obtenemos un resultado diferente:
$$\mathbf{\vec b} - \mathbf{\vec a} = <4-1, 1-2, 4-0>$$
$$\mathbf{\vec b} - \mathbf{\vec a} = <3, -1, 4> = \mathbf{\mathbf{\vec a}b}$$
Observe que el vector $$\mathbf{\vec b} - \mathbf{\vec a}$$ tiene la misma longitud que el vector $$$\mathbf{\vec a} - \mathbf{\vec b}$$, pero va en sentido contrario.
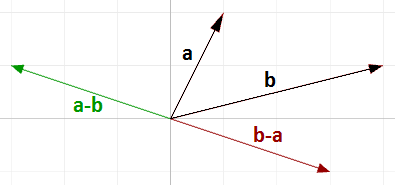
En general, si tenemos dos vectores, $$\mathbf{\vec a}$$ y $$\mathbf{\vec b}$$, entonces $$$\mathbf{\vec a} - \mathbf{\vec b}$$ es un vector que se calcula de la siguiente manera:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a}-\mathbf{\vec b} = <a_1 - b_1, a_2 - b_2, a_3 - b_3> = \mathbf{\mathbf{\vec b}a}$$
La resta de vectores se suele usar para hallar vectores entre puntos. Por lo tanto, si necesitamos hallar un vector que vaya desde el punto extremo del vector de posición $$\mathbf{\vec b}$$ al punto extremo del vector de posición $$\mathbf{\vec a}$$, usamos la resta de vectores $$(\mathbf{\vec a}-\mathbf{\vec b})$$ como se muestra en la Figura (11).
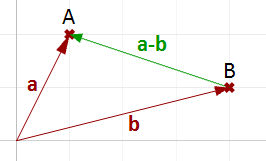
Propiedades de los vectores
Los vectores tienen ocho propiedades fundamentales. Si a, b y c son vectores, y s y t son números, entonces:
$$\mathbf{\vec a} + \mathbf{\vec b} = \mathbf{\vec b} + \mathbf{\vec a}$$
$$\mathbf{\vec a} + 0 = a$$
$$s * (\mathbf{\vec a} + \mathbf{\vec b}) = s * a + s * \mathbf{\vec b}$$
$$s * t * (\mathbf{\vec a}) = s * (t * \mathbf{\vec a})$$
$$\mathbf{\vec a} + (\mathbf{\vec b} + \mathbf{\vec c}) = (\mathbf{\vec a} + \mathbf{\vec b}) + \mathbf{\vec c}$$
$$\mathbf{\vec a} + (-\mathbf{\vec a}) = 0$$
$$(s + t) * \mathbf{\vec a} = s * \mathbf{\vec a} + t * \mathbf{\vec a}$$
$$1 * \mathbf{\vec a} = \mathbf{\vec a}$$
Producto escalar de vectores
El producto escalar toma dos vectores y se obtiene un número. Por ejemplo, si tenemos los dos vectores a y b de modo que:
$$\mathbf{\vec a} = <1, 2, 3> $$
$$\mathbf{\vec b} = <5, 6, 7>$$
Entonces el producto escalar es la suma de multiplicar los componentes de la siguiente manera:
$$\mathbf{\vec a} · \mathbf{\vec b} = 1 * 5 + 2 * 6 + 3 * 7$$
$$\mathbf{\vec a} · \mathbf{\vec b} = 38$$
En general, dados los dos vectores a y b:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a} · \mathbf{\vec b} = a_1 * b_1 + a_2 * b_2 + a_3 * b_3$$
Siempre obtenemos un número positivo del producto escalar entre dos vectores cuando van en la misma dirección general. Un producto escalar negativo entre dos vectores significa que los dos vectores van en la dirección general opuesta.
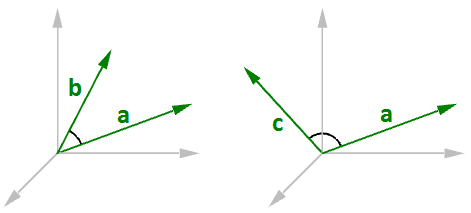
Al calcular el producto escalar de dos vectores unitarios, el resultado siempre está entre 1 y +1. Por ejemplo:
$$\mathbf{\vec a} = <1, 0, 0>$$
$$\mathbf{\vec b} = <0,6, 0,8, 0>$$
$$\mathbf{\vec a} · \mathbf{\vec b} = (1 * 0.6, 0 * 0.8, 0 * 0) = 0.6$$
Además, el producto escalar de un vector consigo mismo es igual a la longitud de ese vector elevado a dos. Por ejemplo:
$$\mathbf{\vec a} = <0, 3, 4>$$
$$\mathbf{\vec a} · \mathbf{\vec a} = 0 * 0 + 3 * 3 + 4 * 4 $$
$$\mathbf{\vec a} · \mathbf{\vec a} = 25$$
Cálculo de la longitud cuadrada del vector $$\mathbf{\vec a}$$:
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5$$
$$\vert \mathbf{\vec a} \vert 2 = 25$$
Producto escalar de vectores, longitudes y ángulos
Existe una relación entre el producto escalar de dos vectores y el ángulo entre ellos.
En general:
$$\mathbf{\vec a} · \mathbf{\vec b} = \vert \mathbf{\vec a} \vert * \vert \mathbf{\vec b} \vert * cos(ө)$$ , o bien
$$\mathbf{\vec a} · \mathbf{\vec b} / (\vert \mathbf{\vec a} \vert * \vert \mathbf{\vec b} \vert) = cos(ө)$$
Donde:
$$ө$$ es el ángulo incluido entre los vectores.
Si los vectores a y b son vectores unitarios, podemos decir que:
$$\mathbf{\vec a} · \mathbf{\vec b} = cos(ө)$$Y dado que el coseno de un ángulo de 90 grados es igual a 0, podemos decir que:
Por ejemplo, si calculamos el producto escalar de los dos vectores ortogonales, el eje x y el eje y universales, el resultado será igual a cero.
$$\mathbf{\vec x} = <1, 0, 0>$$
$$\mathbf{\vec y} = <0, 1, 0>$$
$$\mathbf{\vec x} · \mathbf{\vec y} = (1 * 0) + (0 * 1) + (0 * 0)$$
$$\mathbf{\vec x} · \mathbf{\vec y} = 0$$
También existe una relación entre el producto escalar y la longitud de proyección de un vector sobre otro. Por ejemplo:
$$\mathbf{\vec a} = <5, 2, 0>$$
$$\mathbf{\vec b} = <9, 0, 0>$$
$$unidad(\mathbf{\vec b}) = <1, 0, 0>$$
$$\mathbf{\vec a} · unidad(\mathbf{\vec b}) = (5 * 1) + (2 * 0) + (0 * 0) $$
$$\mathbf{\vec a} - unidad(\mathbf{\vec b}) = 2 (\text{que es igual a la longitud de proyección de mathbf{\vec a} sobre mathbf{\vec b}})$$

En general, dado un vector a y un vector distinto a cero b, podemos calcular la longitud de proyección pL del vector a sobre el vector b utilizando el producto escalar.
$$pL = \vert \mathbf{\vec a} \vert * cos(ө) $$
$$pL = \mathbf{\vec a} · unidad(\mathbf{\vec b})$$
Propiedades del producto escalar
Si $$\mathbf{\vec a}$$, $$\mathbf{\vec b}$$ y $$\mathbf{\vec c}$$ son vectores y s es un número, entonces:
$$\mathbf{\vec a} · \mathbf{\vec a} = \vert \mathbf{\vec a} \vert ^2$$
$$\mathbf{\vec a} · (\mathbf{\vec b} + \mathbf{\vec c}) = \mathbf{\vec a} · \mathbf{\vec b} + \mathbf{\vec a} · \mathbf{\vec c}$$
$$0 · \mathbf{\vec a} = 0$$
$$\mathbf{\vec a} · \mathbf{\vec b} = \mathbf{\vec b} · \mathbf{\vec a}$$
$$(s * \mathbf{\vec a}) · \mathbf{\vec b} = s * (\mathbf{\vec a} · \mathbf{\vec b}) = \mathbf{\vec a} · (s * \mathbf{\vec b})$$
Producto vectorial
El producto vectorial toma dos vectores y se obtiene un tercer vector que es ortogonal a ambos.
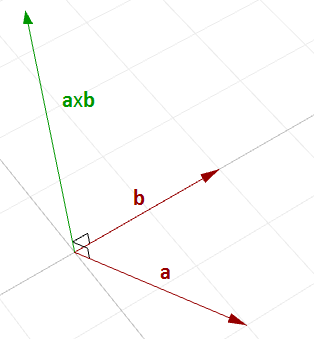
Por ejemplo, si tiene dos vectores que se encuentran en el plano xy universal, entonces su producto vectorial es un vector perpendicular al plano xy que va en la dirección del eje z universal positivo o negativo. Por ejemplo:
$$\mathbf{\vec a} = <3, 1, 0>$$
$$\mathbf{\vec b} = <1, 2, 0>$$
$$\mathbf{\vec a} × \mathbf{\vec b} = < (1 * 0 – 0 * 2), (0 * 1 - 3 * 0), (3 * 2 - 1 * 1) > $$
$$\mathbf{\vec a} × \mathbf{\vec b} = <0, 0, 5>$$
Probablemente nunca tenga que calcular manualmente un producto vectorial de dos vectores, pero si tiene curiosidad sobre cómo se hace, continúe leyendo; si no, puede omitir esta sección. El producto vectorial $$a × b$$ se resuelve utilizando determinantes. Esta ilustración simple muestra cómo calcular un determinante utilizando los vectores base estándar:
$$ \color {red}{i} = <1, 0, 0>$$
$$ \color {blue}{j} = <0,1, 0>$$
$$ \color {green}{k} = <0, 0, 1>$$
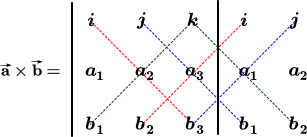
El producto vectorial de los dos vectores $$\mathbf{\vec a} = <a1, a2, a3>$$ y $$\mathbf{\vec b} = <b1, b2, b3>$$ se calcula de la siguiente manera utilizando el diagrama anterior:
$$\mathbf{\vec a} × \mathbf{\vec b} = \color {red}{i (a_2 * b_3)} + \color {blue}{ j (a_3 * b_1)} + \color {green}{k(a_1 * b_2)} - \color {green}{k (a_2 * b_1)} - \color {red}{i (a_3 * b_2)} -\color {blue}{ j (a_1 * b_3)}$$
$$\mathbf{\vec a} × \mathbf{\vec b} = \color {red}{i (a_2 * b_3 - a_3 * b_2)} + \color {blue}{j (a_3 * b_1 - a_1 * b_3)} +\color {green}{k (a_1 * b_2 - a_2 * b_1)}$$
$$\mathbf{\vec a} × \mathbf{\vec b} = <\color {red}{a_2 * b_3 – a_3 * b_2}, \color {blue}{a_3 * b_1 - a_1 * b_3}, \color {green}{a_1 * b_2 - a_2 * b_1} >$$
Producto vectorial y ángulo entre vectores
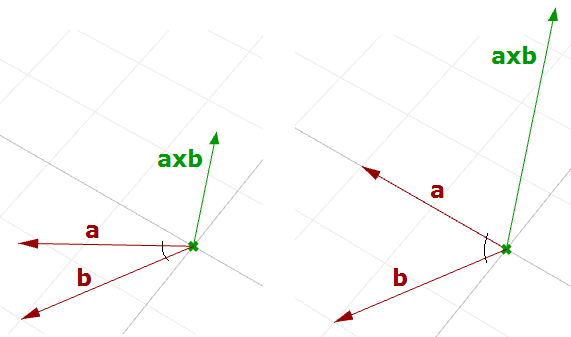
Existe una relación entre el ángulo entre dos vectores y la longitud de su producto vectorial. Cuanto menor sea el ángulo (seno más pequeño), más corto será el producto vectorial. El orden de los operandos es importante en los productos vectoriales. Por ejemplo:
$$\mathbf{\vec a} = <1, 0, 0>$$
$$\mathbf{\vec b} = <0, 1, 0>$$
$$\mathbf{\vec a} × \mathbf{\vec b} = <0, 0, 1>$$
$$\mathbf{\vec b} × \mathbf{\vec a} = <0, 0, -1>$$
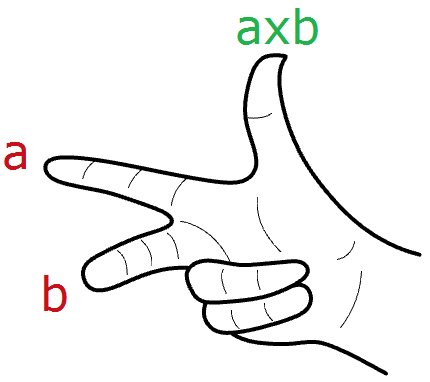
En el sistema diestro de Rhino, la dirección de $$\mathbf{\vec a} × \mathbf{\vec b}$$ viene dada por la regla de la mano derecha (donde $$\mathbf{\vec a}$$ = dedo índice, $$\mathbf{\vec b}$$ = dedo corazón y $$\mathbf{\vec a} × \mathbf{\vec b}$$ = pulgar).
En general, para cualquier par de vectores 3D $$\mathbf{\vec a}$$ y $$\mathbf{\vec b}$$:
$$\vert \mathbf{\vec a} × \mathbf{\vec b} \vert = \vert \mathbf{\vec a} \vert \vert \mathbf{\vec b} \vert sin(ө)$$Donde:
$$ө$$ es el ángulo incluido entre los vectores de posición de $$\mathbf{\vec a}$$ y $$\mathbf{\vec b}$$$
Si a y b son vectores unitarios, entonces podemos decir que la longitud de su producto vectorial es igual al seno del ángulo entre ellos. En otras palabras:
$$\vert \mathbf{\vec a} × \mathbf{\vec b} \vert = sin(ө)$$El producto vectorial entre dos vectores nos ayuda a determinar si dos vectores son paralelos. Esto se debe a que el resultado es siempre un vector cero.
Propiedades del producto vectorial
Si
$$\mathbf{\vec a}$$,
$$\mathbf{\vec b}$$ y
$$\mathbf{\vec c}$$ son vectores, y
$$s$$ es un número, entonces:
$$\mathbf{\vec a} × \mathbf{\vec b} = -\mathbf{\vec b} × \mathbf{\vec a}$$
$$(s * \mathbf{\vec a}) × \mathbf{\vec b} = s * (\mathbf{\vec a} × \mathbf{\vec b}) = \mathbf{\vec a} × (s * \mathbf{\vec b})$$
$$\mathbf{\vec a} × (\mathbf{\vec b} + \mathbf{\vec c}) = \mathbf{\vec a} × \mathbf{\vec b} + \mathbf{\vec a} × \mathbf{\vec c}$$
$$(\mathbf{\vec a} + \mathbf{\vec b}) × \mathbf{\vec c} = \mathbf{\vec a} × \mathbf{\vec c} + \mathbf{\vec b} × \mathbf{\vec c}$$
$$\mathbf{\vec a} · (\mathbf{\vec b} × \mathbf{\vec c}) = (\mathbf{\vec a} × \mathbf{\vec b}) · \mathbf{\vec c}$$
$$\mathbf{\vec a} × (\mathbf{\vec b} × \mathbf{\vec c}) = (\mathbf{\vec a} · \mathbf{\vec c}) * \mathbf{\vec b} – (\mathbf{\vec a} · \mathbf{\vec b}) * \mathbf{\vec c}$$
1.3 Ecuación vectorial de una línea
La ecuación vectorial de una línea se utiliza en aplicaciones de modelado 3D y diseño gráfico por ordenador.
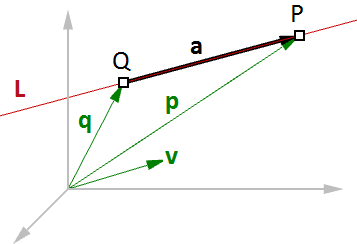
Por ejemplo, si sabemos la dirección de una línea y un punto en esa línea, podemos hallar cualquier otro punto en la línea utilizando vectores, como se muestra a continuación:
$$\overline{L} = line$$
$$\mathbf{\vec v} = <a, b, c>$$ vector unitario de dirección de la línea
$$Q = (x_0, y_0, z_0)$$ punto de posición de la línea
$$P = (x, y, z)$$ cualquier punto en la línea
Sabemos que:
$$\mathbf{\vec a} = t *\mathbf{\vec v}$$ (2)
$$\mathbf{\vec p} = \mathbf{\vec q} + \mathbf{\vec a}$$ (1)
A partir de 1 y 2:
$$\mathbf{\vec p} = \mathbf{\vec q} + t * \mathbf{\vec v}$$ (3)
Sin embargo, también podemos expresar (3) de la siguiente manera:
$$<x, y, z> = <x_0, y_0, z_0> + <t * a, t * b, t * c>$$
$$<x, y, z> = <x_0 + t * a, y_0 + t * b, z_0 + t * c>$$
Por tanto:
$$x = x_0 + t * a$$
$$y = y_0 + t * b$$
$$z = z_0 + t * c$$
Que es lo mismo que:
$$P = Q + t * \mathbf{\vec v}$$Otro ejemplo común es hallar el punto medio entre dos puntos. A continuación, se muestra cómo encontrar el punto medio utilizando la ecuación vectorial de una línea:
$$\mathbf{\vec q}$$ es el vector de posición del punto
$Q$$
$$\mathbf{\vec p}$$ es el vector de posición del punto
$$P$$
$$\mathbf{\vec a}$$ es el vector que va desde
$$Q \rightarrow P$$
De la resta de vectores se obtiene que:
$$\mathbf{\vec a} = \mathbf{\vec p} - \mathbf{\vec q}$$De la ecuación lineal se obtiene que:
$$M = Q + t * \mathbf{\vec a}$$Y como necesitamos hallar el punto medio, entonces:
$$t = 0.5$$Por tanto, podemos decir que:
$$M = Q + 0.5 * \mathbf{\vec a}$$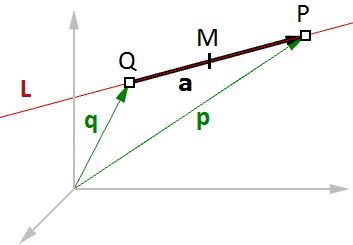
En general, puede hallar cualquier punto entre $$Q$$ y $$P$$ cambiando el valor $$t$$ entre 0 y 1 utilizando la ecuación general:
$$M = Q + t * (P - Q)$$1.4 Ecuación vectorial de un plano
Una forma de definir un plano es cuando hay un punto y un vector que es perpendicular al plano. Ese vector generalmente se conoce como normal al plano. La normal apunta en la dirección por encima del plano.
Un ejemplo de cómo calcular la normal de un plano es cuando hay tres puntos no lineales en el plano.
En la Figura (16), dados:
$$A$$ = el primer punto del plano
$$B$$ = el segundo punto del plano
$$C$$ = el tercer punto del plano
Y:
$$\mathbf{\vec a} $$ = un vector de posición del punto
$$A$$
$$\mathbf{\vec b}$$ = un vector de posición del punto
$$B$$
$$\mathbf{\vec c}$$ = un vector de posición del punto
$$C$$
Podemos encontrar el vector de la normal $$\mathbf{\vec n}$$ de la siguiente manera:
$$\mathbf{\vec n} = (\mathbf{\vec b} - \mathbf{\vec a}) × (\mathbf{\vec c} - \mathbf{\vec a})$$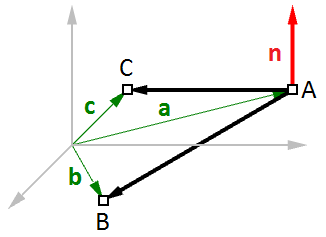
También podemos derivar la ecuación escalar del plano utilizando el producto escalar del vector:
$$\mathbf{\vec n} · (\mathbf{\vec b} - \mathbf{\vec a}) = 0$$Si:
$$\mathbf{\vec n} = <a, b, c>$$
$$\mathbf{\vec b} = <x, y, z>$$
$$ \mathbf{\vec a} = <x_0, y_0, z_0>$$
Entonces podemos ampliar lo anterior:
$$<a, b, c> · <x-x_0, y-y_0, z-z_0 > = 0$$Resolver el producto escalar da la ecuación escalar general de un plano:
$$a * (x - x_0) + b * (y - y_0) + c * (z - z_0) = 0$$1.5 Tutoriales
Todos los conceptos tratados en este capítulo tienen una aplicación directa para resolver problemas geométricos comunes que se encuentran durante el modelado. Los siguientes tutoriales paso a paso emplean los conceptos aprendidos en este capítulo utilizando Rhinoceros y Grasshopper (GH).
1.5.1 Dirección de cara
Dados un punto y una superficie, ¿cómo podemos determinar si el punto está orientado hacia la parte frontal o posterior de esa superficie?
Entrada:
- Una superficie
- Un punto
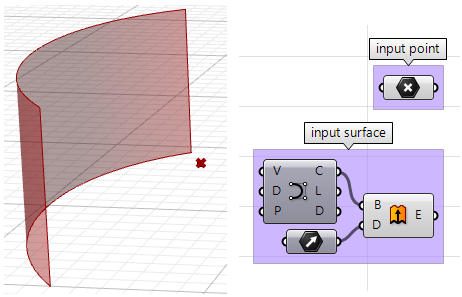
Parámetros:
La dirección de la cara está definida por la dirección normal de la superficie. Necesitaremos la siguiente información:
- La dirección normal de la superficie en una ubicación de superficie más cercana al punto de entrada.
- Una dirección de vector desde el punto más cercano al punto de entrada.
Compare las dos direcciones anteriores. Si van en la misma dirección, el punto está orientado hacia la parte frontal; de lo contrario, está orientado hacia la parte posterior.
Solución:
1. Encuentre la ubicación del punto más cercano en la superficie en relación con el punto de entrada utilizando el componente Pull. Esto nos dará la ubicación uv del punto más cercano, que luego podemos usar para evaluar la superficie y hallar su dirección normal.
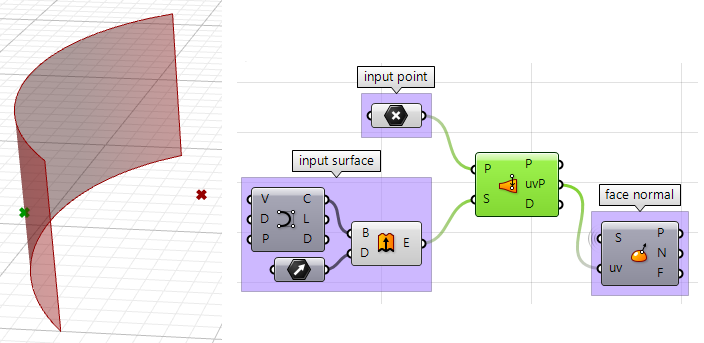
2. Ahora podemos usar el punto más cercano para dibujar un vector orientado hacia el punto de entrada. También podemos dibujar:
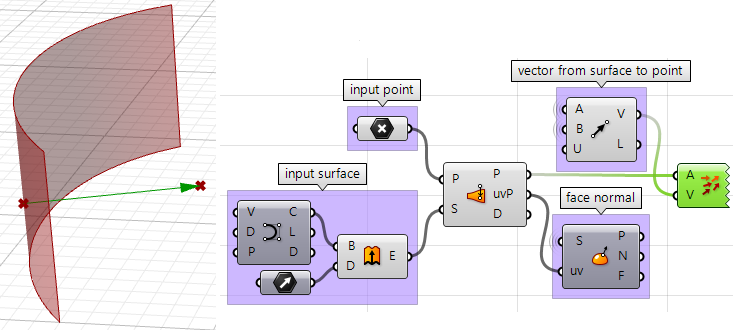
3. Podemos comparar los dos vectores utilizando el producto escalar. Si el resultado es positivo, el punto está delante de la superficie. Si el resultado es negativo, el punto está detrás de la superficie.
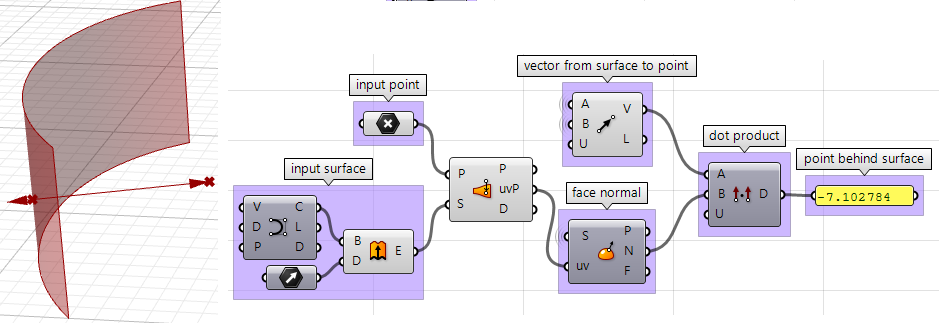
Los pasos anteriores también se pueden resolver utilizando otros lenguajes de scripting. Uso del componente VB de Grasshopper:
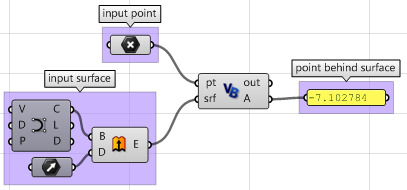
Private Sub RunScript(ByVal pt As Point3d, ByVal srf As Surface, ByRef A As Object)
'Declare variables
Dim u, v As Double
Dim closest_pt As Point3d
'get closest point u, v
srf.ClosestPoint(pt, u, v)
'get closest point
closest_pt = srf.PointAt(u, v)
'calculate direction from closest point to test point
Dim dir As New Vector3d(pt - closest_pt)
'calculate surface normal
Dim normal = srf.NormalAt(u, v)
'compare the two directions using the dot product
A = dir * normal
End Sub
Uso del componente Python de Grasshopper con RhinoScriptSyntax:
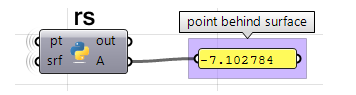
import rhinoscriptsyntax as rs #import RhinoScript library
#find the closest point
u, v = rs.SurfaceClosestPoint(srf, pt)
#get closest point
closest_pt = rs.EvaluateSurface(srf, u, v)
#calculate direction from closest point to test point
dir = rs.PointCoordinates(pt) - closest_pt
#calculate surface normal
normal = rs.SurfaceNormal(srf, [u, v])
#compare the two directions using the dot product
A = dir * normal
Uso del componente Python de Grasshopper solo con RhinoCommon:
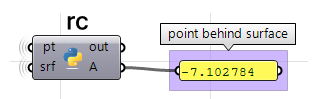
#find the closest point
found, u, v = srf.ClosestPoint(pt)
if found:
#get closest point
closest_pt = srf.PointAt(u, v)
#calculate direction from closest point to test point
dir = pt - closest_pt
#calculate surface normal
normal = srf.NormalAt(u, v)
#compare the two directions using the dot product
A = dir * normal
Uso del componente C# de Grasshopper:

private void RunScript(Point3d pt, Surface srf, ref object A)
{
//Declare variables
double u, v;
Point3d closest_pt;
//get closest point u, v
srf.ClosestPoint(pt, out u, out v);
//get closest point
closest_pt = srf.PointAt(u, v);
//calculate direction from closest point to test point
Vector3d dir = pt - closest_pt;
//calculate surface normal
Vector3d normal = srf.NormalAt(u, v);
//compare the two directions using the dot product
A = dir * normal;
}
1.5.2 Caja descompuesta
El siguiente tutorial muestra cómo descomponer una polisuperficie. Así es como queda la caja descompuesta al final:
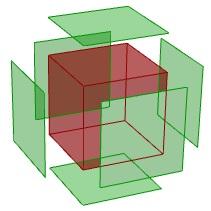
Entrada:
Identifique la entrada, que es una caja.

Parámetros:
- Piense en todos los parámetros que tenemos que conocer para este tutorial.
- El centro de la descomposición.
- Las caras de la caja que estamos descomponiendo.
- La dirección hacia la que se mueve cada cara.
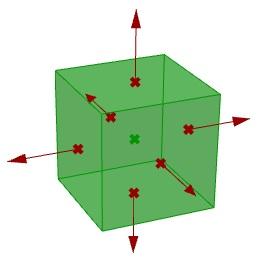
Una vez identificados los parámetros, es cuestión de juntarlos en una solución uniendo los pasos lógicos para lograr una respuesta.
Solución:
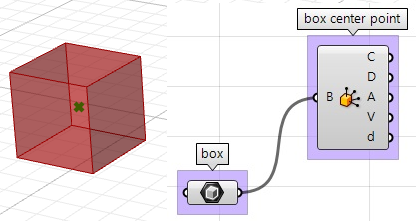
1. Encuentre el centro de la caja utilizando el componente Box Properties en GH:
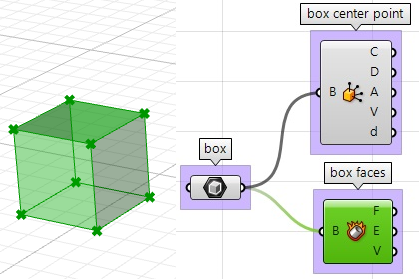
2. Extraiga las caras de la caja con el componente Deconstruct Brep:
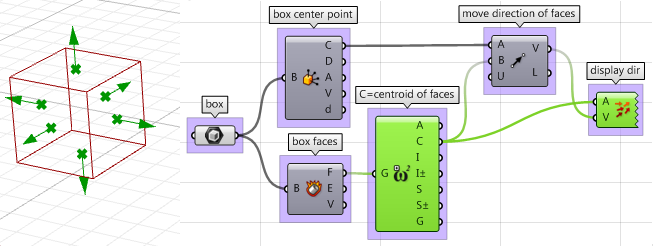
3. La dirección hacia la que movemos las caras es la parte complicada. Primero debemos encontrar el centro de cada cara y luego definir la dirección desde el centro de la caja hacia el centro de cada cara de la siguiente manera:
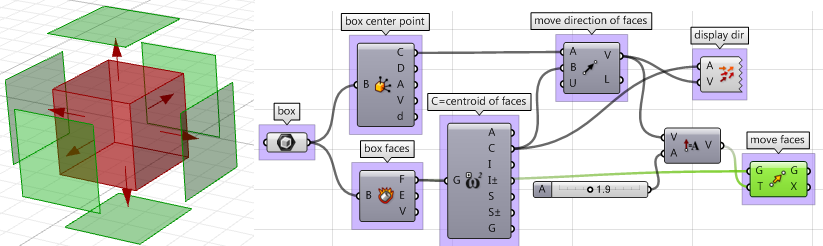
4. Una vez tengamos todos los parámetros listos, podemos usar el componente Move para mover las caras en la dirección adecuada. Asegúrese de configurar la amplitud deseada de los vectores y ya podrá empezar.
Los pasos anteriores también se pueden resolver mediante VB script, C# o Python. A continuación se muestra la solución con estos lenguajes de scripting.
Uso del componente VB de Grasshopper:
Private Sub RunScript(ByVal box As Brep, ByVal dis As Double, ByRef A As Object)
'get the brep center
Dim area As Rhino.Geometry.AreaMassProperties
area = Rhino.Geometry.AreaMassProperties.Compute(box)
Dim box_center As Point3d
box_center = area.Centroid
'get a list of faces
Dim faces As Rhino.Geometry.Collections.BrepFaceList = box.Faces
'decalre variables
Dim center As Point3d
Dim dir As Vector3d
Dim exploded_faces As New List( Of Rhino.Geometry.Brep )
Dim i As Int32
'loop through all faces
For i = 0 To faces.Count() - 1
'extract each of the face
Dim extracted_face As Rhino.Geometry.Brep = box.Faces.ExtractFace(i)
'get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face)
center = area.Centroid
'calculate move direction (from box centroid to face center)
dir = center - box_center
dir.Unitize()
dir *= dis
'move the extracted face
extracted_face.Transform(Transform.Translation(dir))
'add to exploded_faces list
exploded_faces.Add(extracted_face)
Next
'assign exploded list of faces to output
A = exploded_faces
End Sub
Uso del componente Python de Grasshopper con RhinoCommon:
import Rhino
#get the brep center
area = Rhino.Geometry.AreaMassProperties.Compute(box)
box_center = area.Centroid
#get a list of faces
faces = box.Faces
#decalre variables
exploded_faces = []
#loop through all faces
for i, face in enumerate(faces):
#get a duplicate of the face
extracted_face = faces.ExtractFace(i)
#get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face)
center = area.Centroid
#calculate move direction (from box centroid to face center)
dir = center - box_center
dir.Unitize()
dir *= dis
#move the extracted face
move = Rhino.Geometry.Transform.Translation(dir)
extracted_face.Transform(move)
#add to exploded_faces list
exploded_faces.append(extracted_face)
#assign exploded list of faces to output
A = exploded_faces
Uso del componente C# de Grasshopper:
private void RunScript(Brep box, double dis, ref object A)
{
//get the brep center
Rhino.Geometry.AreaMassProperties area = Rhino.Geometry.AreaMassProperties.Compute(box);
Point3d box_center = area.Centroid;
//get a list of faces
Rhino.Geometry.Collections.BrepFaceList faces = box.Faces;
//decalre variables
Point3d center; Vector3d dir;
List<Rhino.Geometry.Brep> exploded_faces = new List<Rhino.Geometry.Brep>();
//loop through all faces for( int i = 0; i < faces.Count(); i++ )
{
//extract each of the face
Rhino.Geometry.Brep extracted_face = box.Faces.ExtractFace(i);
//get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face);
center = area.Centroid;
//calculate move direction (from box centroid to face center)
dir = center - box_center;
dir.Unitize();
dir *= dis;
//move the extracted face
extracted_face.Transform(Transform.Translation(dir));
//add to exploded_faces list
exploded_faces.Add(extracted_face);
}
//assign exploded list of faces to output
A = exploded_faces;
}
1.5.3 Esferas tangentes
Este tutorial muestra cómo crear dos esferas tangentes entre dos puntos de entrada. El resultado será el siguiente:
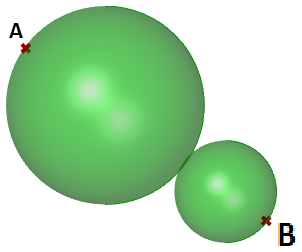
Entrada:
Dos puntos (
$$A$$ y
$$B$$) en el sistema de coordenadas 3D.
Parámetros: A continuación, se muestra un diagrama de los parámetros que necesitaremos para resolver el problema: $$A$$ punto tangente $$D$$ entre las dos esferas, en algún parámetro $$t$$ (0-1) entre los puntos $$A$$ y $$B$$.
- El centro de la primera esfera o el punto medio $$C1$$ entre $$A$$ y $$D$$.
- El centro de la segunda esfera o el punto medio $$C2$$ entre $$D$$ y $$B$$.
- El radio de la primera esfera $$(r1)$$ o la distancia entre $$A$$ y $$C1$$.
- El radio de la segunda esfera $$(r2)$$ o la distancia entre $$D$$ y $$C2$$.
Solución:
1. Utilice el componente Expression para definir el punto $$D$$ entre $$A$$ y $$B$$ como parámetro $$t$$. La expresión que usaremos se basa en la ecuación vectorial de una línea:
$$D = A + t*(B-A)$$$$B-A$$ : es el vector que va de $$B$$ a
$$A (\vec{BA}) mediante la operación de resta de vectores.
$$
t*(B-A) $$: donde $$t$$ está entre 0 y 1 para obtener una ubicación en el vector.
$$
A+t*(B-A)$$ : obtiene un punto en el vector entre A y B.
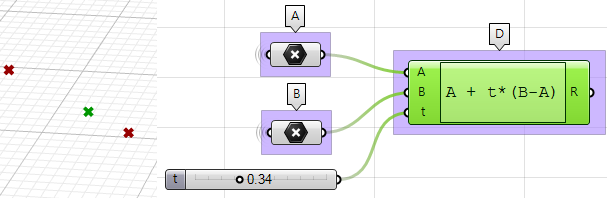
2. Utilice el componente Expression para definir también los puntos medios $$
C1 $$ y $$C2$$.
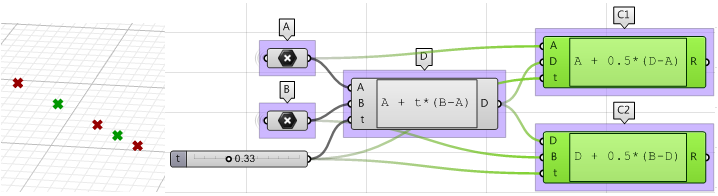
3. El radio de la primera esfera $$
(r1) $$ y el radio de la segunda esfera $$(r2)$$ se pueden calcular utilizando el componente Distance.
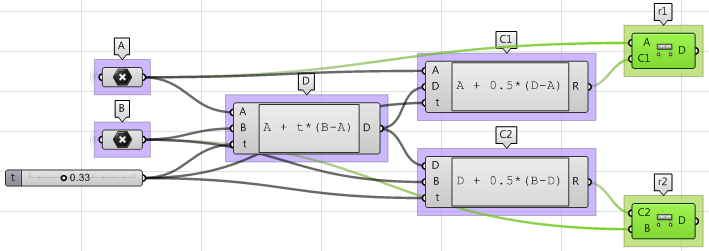
4. El último paso consiste en crear la esfera a partir de un plano base y un radio. Debemos asegurarnos de que los orígenes estén conectados a $$
C1 $$ y $$C2 $$ y al radio de $$r1 $$ y $$r2$$.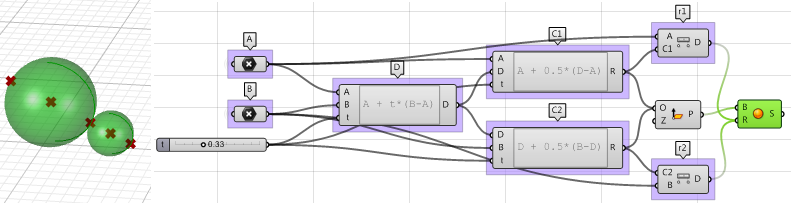
Uso del componente VB de Grasshopper:
Private Sub RunScript(ByVal A As Point3d, ByVal B As Point3d, ByVal t As Double, ByRef S1 As Object, ByRef S2 As Object)
'declare variables
Dim D, C1, C2 As Rhino.Geometry.Point3d
Dim r1, r2 As Double
'find a point between A and B
D = A + t * (B - A)
'find mid point between A and D
C1 = A + 0.5 * (D - A)
'find mid point between D and B
C2 = D + 0.5 * (B - D)
'find spheres radius
r1 = A.DistanceTo(C1)
r2 = B.DistanceTo(C2)
'create spheres and assign to output
S1 = New Rhino.Geometry.Sphere(C1, r1)
S2 = New Rhino.Geometry.Sphere(C2, r2)
End Sub
Uso del componente Python:
import Rhino
#find a point between A and B
D = A + t * (B - A)
#find mid point between A and D
C1 = A + 0.5 * (D - A)
#find mid point between D and B
C2 = D + 0.5 * (B - D)
#find spheres radius
r1 = A.DistanceTo(C1)
r2 = B.DistanceTo(C2)
#create spheres and assign to output
S1 = Rhino.Geometry.Sphere(C1, r1)
S2 = Rhino.Geometry.Sphere(C2, r2)
Uso del componente C# de Grasshopper:
private void RunScript(Point3d A, Point3d B, double t, ref object S1, ref object S2)
{
//declare variables
Rhino.Geometry.Point3d D, C1, C2;
double r1, r2;
//find a point between A and B
D = A + t * (B - A);
//find mid point between A and D
C1 = A + 0.5 * (D - A);
//find mid point between D and B
C2 = D + 0.5 * (B - D);
//find spheres radius
r1 = A.DistanceTo(C1);
r2 = B.DistanceTo(C2);
//create spheres and assign to output
S1 = new Rhino.Geometry.Sphere(C1, r1);
S2 = new Rhino.Geometry.Sphere(C2, r2);
}
Descargar archivos de muestra
Descargue el archivo math-samplesandtutorials.zip , que contiene todos los archivos de ejemplo de Grasshopper y de código de esta guía.
Próximos pasos
Ahora que ya conoce las matemáticas vectoriales, consulte la guía Matrices y transformaciones para aprender más sobre mover, rotar y escalar objetos….

