Les transformations correspondent aux opérations telles que le déplacement (également appelé translation), la rotation et le changement d’échelle d’objets. Elles sont enregistrées en programmation 3D à l’aide de matrices, qui sont tout simplement des tableaux rectangulaires de nombres. Les matrices peuvent être utilisées pour appliquer très rapidement plusieurs transformations. En effet, une matrice [4x4] peut représenter toutes les transformations. L’utilisation d’une taille de matrice unique pour toutes les transformations permet de réduire les temps de calcul.
$$\begin{array}{rcc} \mbox{matrice}&\begin{array}{cccc} c1& c2&c3&c4\end{array}\\\begin{array}{c}ligne(1)\\ligne(2)\\ligne(3)\\ligne(4)\end{array}& \left[\begin{array}{cr} +&+&+&+\\ +&+&+&+\\ +&+&+&+\\ +&+&+&+\end{array}\right] \end{array}$$2.1 Opérations matricielles
L’opération la plus importante en infographie est le produit matriciel. Nous l’expliquerons de manière détaillée ici.
Produit matriciel
Le produit matriciel est utilisé pour appliquer des transformations sur une géométrie. Par exemple, afin de faire tourner un point autour d’un axe, on peut utiliser une matrice de rotation et la multiplier par le point.
$$\begin{array}{ccc} \text{matrice de rotation} & \text{point d’entrée} & \text{point de rotation}\\\begin{bmatrix}a & b & c & d \\e & f & g & h \\i & j & k & l \\0 & 0 & 0 & 1 \\\end{bmatrix}& \cdot\begin{bmatrix}x \\y\\z\\1 \\\end{bmatrix}&= \begin{bmatrix}x' \\y'\\z'\\1 \\\end{bmatrix}\end{array}$$La plupart du temps, plusieurs transformations doivent être appliquées à la même géométrie. Par exemple, pour déplacer et faire pivoter des milliers de points, on peut utiliser une des méthodes suivantes :
Méthode 1
- Multiplier la matrice de déplacement par les 1 000 points pour les déplacer.
- Multiplier la matrice de rotation par les 1 000 points obtenus afin de les faire pivoter.
Nombre d’opérations = 2 000.
Méthode 2
- Multiplier les matrices de rotation et de déplacement pour créer une matrice de transformation combinée.
- Multiplier la matrice combinée par les 1 000 points pour les déplacer et les faire pivoter en une seule opération.
Nombre d’opérations = 1 001.
La première méthode nécessite presque deux fois plus d’opérations pour arriver au même résultat. Même si la deuxième méthode est plus efficace, elle n’est possible que si les deux matrices sont $$[4 \times 4]$$. C’est pour cette raison que toutes les transformations sont représentées par des matrices $$[4 \times 4]$$ en infographie alors que les points sont représentés par une matrice $$[4 \times 1]$$.
Les applications de modélisation en trois dimensions possèdent des outils pour appliquer des transformations et multiplier des matrices, mais si vous voulez savoir comment multiplier des matrices en mathématiques, voici un exemple simple : Afin de pouvoir multiplier deux matrices, leurs dimensions doivent correspondre. Ainsi, le nombre de colonnes de la première matrice doit être égal au nombre de lignes de la deuxième matrice. La matrice résultante possède autant de lignes que la première matrice et autant de colonnes que la deuxième. Par exemple, soient deux matrices $$M$$ et $$P$$, de dimensions $$[4\times 4]$$ et $$[4 \times 1]$$ respectivement, les dimensions de la matrice résultant du produit $$M · P$$ seront de $$[4 \times 1]$$ comme le montre l’illustration suivante :
$$\begin{array}{ccc} M & P & P' \\\begin{bmatrix}\color{red}{a} & \color{red}{b} & \color{red}{c} & \color{red}{d} \\e & f & g & h \\i & j & k & l \\0 & 0 & 0 & 1 \\\end{bmatrix}& \cdot\begin{bmatrix}\color{red}{x} \\\color{red}{y} \\\color{red}{z} \\\color{red}{1} \\\end{bmatrix}&= \begin{bmatrix}\color{red}{x'=a*x+b*y+c*z+d*1}\\y'=e*x+f*y+g*z+h*1\\z'=i*x+j*y+k*z+l*1 \\1=0*x+0*y+0*z+1*1\\\end{bmatrix}\end{array}$$Matrice identité
La matrice identité est une matrice spéciale dont tous les composants de la diagonale sont 1 et les autres 0.
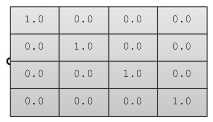
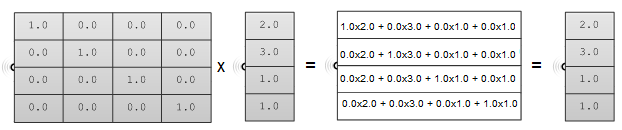
La principale propriété d’une matrice identité est le fait que les valeurs multipliées par zéro ne changent pas lorsqu’elle est multipliée par une autre matrice.
2.2 Opérations de transformation
La plupart des transformations conservent les relations de parallélisme entre les éléments de géométrie. Les points colinéaires restent colinéaires après la transformation par exemple. Les points se trouvant sur un même plan restent également coplanaires après la transformation. Ce type de transformation est appelé une transformation affine.
Transformation de translation (déplacement)
Le déplacement d’un point depuis une position de départ selon un vecteur peut être calculé ainsi :
$$P’ = P + \mathbf{\vec v}$$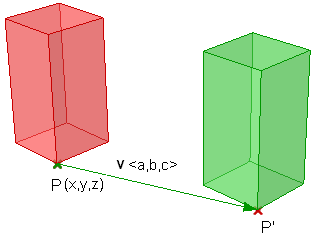
Soit :
$$P(x,y,z)$$ un point donné
$$\mathbf{\vec v}=<a,b,c>$$ un vecteur de translation
Alors :
$$P’(x) = x + a$$
$$P’(y) = y + b$$
$$P’(z) = z + c$$
Les points sont représentés dans une matrice [4x1] avec un 1 dans la dernière ligne. Le point P(x,y,z) par exemple est représenté ainsi :
$$\begin{bmatrix}x\\y\\z\\1\\\end{bmatrix}$$L’utilisation d’une matrice $$[4 \times 4]$$ pour les transformations (appelée système de coordonnées homogènes), au lieu d’une matrice $$[3 \times 3]$$, permet de représenter toutes les transformations, y compris la translation. Format général d’une matrice de translation :
$$\begin{bmatrix}1 & 0 & 0 & \color{red}{a1} \\0 & 1 & 0 & \color{red}{a2} \\0 & 0 & 1 & \color{red}{a3} \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Par exemple, si le point $$P(2,3,1)$$ est déplacé selon le vecteur $$\vec v <2,2,2>$$, sa nouvelle position sera :
$$P’ = P + \mathbf{\vec v} = (2+2, 3+2, 1+2) = (4, 5, 3)$$En utilisant la forme matricielle et en multipliant la matrice de translation par le point de départ, la nouvelle position du point est déterminée ainsi :
$$\begin{bmatrix}1 & 0 & 0 & 2 \\0 & 1 & 0 & 2 \\0 & 0 & 1 & 2 \\0 & 0 & 0 & 1 \\\end{bmatrix}\cdot\begin{bmatrix}2 \\3\\1\\1 \\\end{bmatrix}= \begin{bmatrix}(1*2 + 0*3 + 0*1 + 2*1) \\(0*2 + 1*3 + 0*1 + 2*1)\\(0*2 + 0*3 + 1*1 + 2*1)\\(0*2 + 0*3 + 0*1 + 1*1)\\\end{bmatrix}=\begin{bmatrix}4 \\5\\3\\1 \\\end{bmatrix}$$De même, la translation d’une géométrie quelconque peut se faire en multipliant ses points de construction par la matrice de translation. Par exemple, étant donnée une boîte définie par huit sommets que l’on veut déplacer de 4 unités dans la direction x, 5 unités dans la direction y et 3 unités dans la direction z, on doit multiplier chacun des huit sommets par la matrice de translation suivante pour obtenir la nouvelle boîte :
$$\begin{bmatrix}1 & 0 & 0 & 4\\ 0 & 1 & 0 & 5 \\0 & 0 & 1 & 3 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$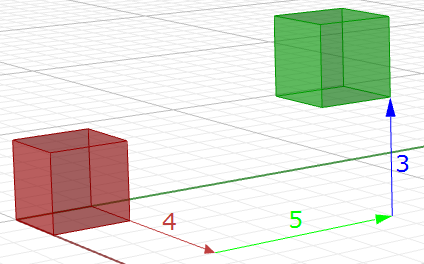
Transformation de rotation
Cette section montre comment calculer la rotation autour de l’axe des z et de l’origine en utilisant la trigonométrie puis comment déduire le format général de la matrice de rotation.
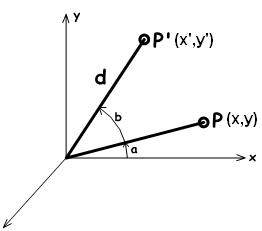
Prenons un point $$P(x,y)$$ sur le plan $$x,y$$ et une rotation par l’angle ( $$b$$). À partir de la figure on peut dire que :
$$x = d cos(a)$$ (1)
$$y = d sin(a)$$ (2)
$$x’ = d cos(b+a)$$ (3)
$$y’ = d sin(b+a)$$ (4)
En développant
$$x$$’ et
$$y’$$ à l’aide des identités trigonométriques pour le sinus et le cosinus de la somme des angles :
$$x’ = d cos(a)cos(b) - d sin(a)sin(b)$$ (5)
$$y’ = d cos(a)sin(b) + d sin(a)cos(b)$$ (6)
En utilisant les équations 1 et 2 :
$$x’ = x cos(b) - y sin(b)$$
y’ = x sin(b) + y cos(b)
La matrice de rotation autour de l’axe des z devient :
$$\begin{bmatrix}\color{red}{\cos{b}} & \color{red}{-\sin{b}} & 0 & 0 \\\color{red}{\sin{b}} & \color{red}{\cos{b}} & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$La matrice de rotation autour de l’axe des x selon l’angle $$b$$ devient :
$$\begin{bmatrix}1 & 0 & 0 & 0 \\0 & \color{red}{\cos{b}} & \color{red}{-\sin{b}} & 0 \\0 & \color{red}{\sin{b}} & \color{red}{\cos{b}} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$La matrice de rotation autour de l’axe des y selon l’angle $$b$$ devient :
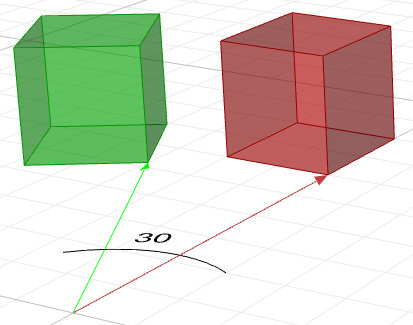
$$\begin{bmatrix}\color{red}{\cos{b}} &0 & \color{red}{\sin{b}} & 0 \\0 & 1 & 0 & 0 \\\color{red}{-\sin{b}} & 0 &\color{red}{\cos{b}} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Par exemple, si on veut faire pivoter une boîte de 30 degrés, on doit :
1. Construire la matrice de rotation de 30 degrés. À l’aide de la forme générale et des valeurs du cosinus et du sinus de l’angle de 30 degrés, la matrice de rotation deviendra :
$$\begin{bmatrix}0.87 & -0.5 & 0 & 0 \\0.5 & 0.87 & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$2. Multiplier la matrice de rotation par la géométrie de départ ou, dans le cas d’une boîte, par chaque sommet pour trouver la nouvelle position de la boîte.
Changement d’échelle
Afin de changer l’échelle d’une géométrie, nous avons besoin d’un facteur d’échelle et d’un point de référence. Le facteur d’échelle peut définir une échelle uniforme dans les directions x, y et z ou être différent pour chaque dimension.
L’échelle d’un point peut utiliser l’équation suivante :
$$P’ = FacteurÉchelle(S) * P$$
Ou :
$$P’.x = Sx * P.x$$
$$P’.y = Sy * P.y$$
$$P’.z = Sz * P.z$$
Cette matrice correspond à une transformation de changement d’échelle dont le centre est l’origine du repère général (0,0,0).
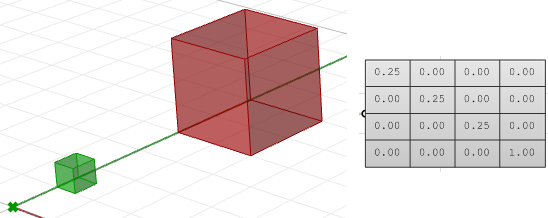
$$\begin{bmatrix}\color{red}{Échelle-x} & 0 & 0 & 0 \\0 & \color{red}{Échelle-y} & 0 & 0 \\0 & 0 & \color{red}{Échelle-z} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Par exemple, si l’on veut appliquer une échelle de 0,25 à une boîte par rapport à l’origine du repère général, la matrice de l’échelle deviendra :
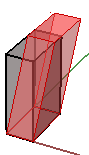
Transformation de cisaillement
Le cisaillement en 3D est mesuré le long de deux axes par rapport à un troisième axe. Par exemple, un cisaillement le long de l’axe des z ne modifiera pas la géométrie le long de cet axe mais le fera sur les axes x et y. Voici quelques exemples de matrices de cisaillement :
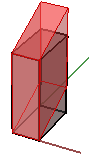
1. Cisaillement sur x et z avec conservation de la coordonnée y :
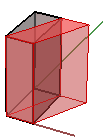$$\begin{bmatrix}1.0 &\color{red}{0.5} & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 &\color{red}{0.5} & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
2. Cisaillement sur y et z avec conservation de la coordonnée x :
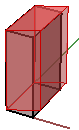$$\begin{bmatrix}1.0 & \color{red}{0.5} & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
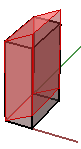$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & \color{red}{0.5} & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
3. Cisaillement sur x et y avec conservation de la coordonnée z :
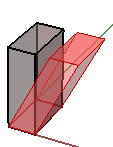$$\begin{bmatrix}1.0 & 0.0 & \color{red}{0.5} & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & \color{red}{0.5} & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
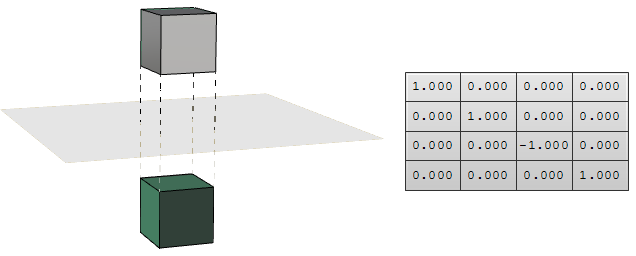
Transformation de symétrie et réflexion
La transformation de symétrie crée le reflet d’un objet par rapport à une ligne ou à un plan. Les objets 2D sont reflétés par rapport à une ligne alors que les objets 3D sont reflétés par rapport à un plan. N’oubliez pas que la transformation de symétrie inverse la direction normale des faces de la géométrie.
Transformation de projection plane
Intuitivement, le point de projection d’un point 3D donné $$P(x,y,z)$$ dans le plan xy du repère général correspond à $$P_{xy} (x,y,0)$$, avec la valeur z définie sur zéro. De même, une projection sur le plan xz d’un point P devient $$P_{xz}(x,0,z)$$. Lors de la projection sur le plan yz, $$P_{xz} = (0,y,z)$$. Ces transformations sont appelées projections orthogonales.
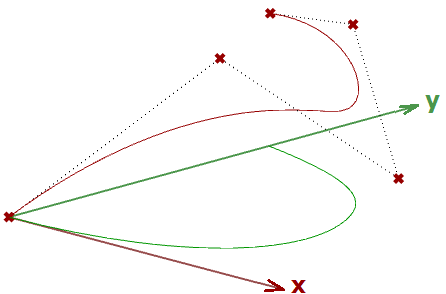
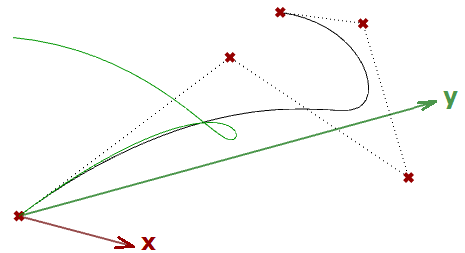
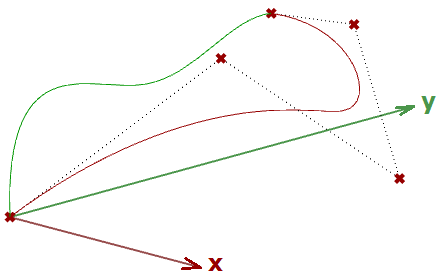
Si l’objet de départ est une courbe à laquelle on applique une transformation de projection plane, on obtient une courbe projetée sur ce plan. L’exemple suivant montre la projection d’une courbe sur le plan xy en utilisant une matrice.
Remarque : Les courbes NURBS (expliquées dans le chapitre suivant) utilisent des points de contrôle pour leur définition. La projection d’une courbe revient à projeter ses points de contrôle.
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & \color{red}{0.0} & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & \color{red}{0.0} & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix} \color{red}{0.0} & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
Téléchargement de fichiers d’exemple
Téléchargez le fichier Fondements mathématiques, qui contient tous les exemples de Grasshopper et les fichiers de code de ce guide.
Étapes suivantes
Maintenant que vous en savez plus sur les matrices et la transformation, consultez le guide Courbes et surfaces paramétriques pour en savoir plus sur la structure détaillée des courbes et surfaces NURBS.
