Imaginons que vous vous déplacez du lundi au vendredi jusqu’à votre lieu de travail. Vous partez à 8 h du matin et arrivez à 9 h. À chaque instant entre 8 h et 9 h, vous vous trouverez à un point sur votre trajet. Si vous dessinez votre position toutes les minutes tout au long de votre trajet, vous pouvez définir le chemin entre votre domicile et votre travail en reliant les 60 points que vous avez tracés. Admettons que vous voyagiez à la même vitesse exactement chaque jour, à 8 h vous seriez chez vous (point de départ), à 9h au travail (point final) et à 8 h 40 à l’endroit exact du chemin où se trouve le 40ème point tracé. Félicitations, vous venez de créer votre première courbe paramétrique ! Vous avez utilisé le temps comme paramètre pour définir votre chemin et vous pouvez donc appeler la courbe de votre trajet une courbe paramétrique. L’intervalle de temps que vous avez passé entre le point de départ et le point final (de 8 à 9 h) est appelé domaine de la courbe ou intervalle.
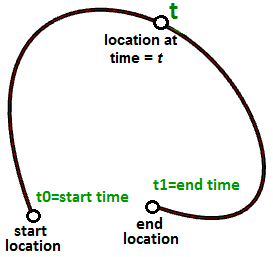
Par définition, on peut décrire la position
$$x$$,
$$y$$ et
$$z$$ d’une courbe paramétrique à partir d’un paramètre
$$t$$ ainsi :
$$x = x(t)$$
$$y = y(t)$$
$$z = z(t)$$
Où :
$$t$$ est une gamme de nombre réels.
Nous avons vu plus tôt que l’équation paramétrique d’une ligne utilisant le paramètre $$t$$ est définie ainsi :
$$x = x’ + t * a$$
$$y = y’ + t * b$$
$$z = z’ + t * c$$
Où :
$$x$$, $$y$$ et $$z$$ sont des fonctions de t où t représente une gamme de nombres réels. $$x’$$, $$y’$$ et $$z’$$ sont les coordonnées d’un point sur le segment de ligne. $$a$$, $$b$$ et $$c$$ définissent la pente de la ligne, de sorte que le vecteur $$\mathbf{\vec v} <a, b, c>$$ soit parallèle à la ligne.
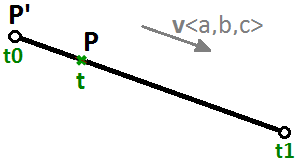
On peut alors écrire l’équation paramétrique d’un segment de ligne en utilisant un paramètre $$t$$ entre $$t0$$ et $$t1$$ (deux nombres réels) et un vecteur unitaire $$\mathbf{\vec v}$$ dans la direction de ligne :
$$P = P’ + t * \mathbf{\vec v}$$Étudions un autre exemple : le cercle. L’équation paramétrique d’un cercle sur le plan xy dont le centre se trouve à l’origine (0,0) et dont le paramètre d’angle $$t$$ se trouve entre et $$0$$ et $$2π$$ radians est :
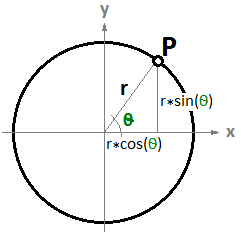
$$x = r \dot cos(t)$$
$$y = r \dot sin(t)$$
On peut dériver l’équation générale d’un cercle pour obtenir l’équation paramétrique de cette façon :
$$ x/r = cos(t)$$
$$y/r = sin(t)$$
Et puisque :
$$cos(t)^2 + sin(t)^2 = 1$$ (identité de Pythagore)
Alors :
$$(x/r)^2 + (y/r)^2 = 1$$, ou
$$x^2 + y^2 = r^2$$
3.1 Courbes paramétriques
Paramètre de la courbe
Un paramètre sur une courbe représente l’adresse d’un point sur cette courbe. Comme indiqué, vous pouvez considérer une courbe paramétrique comme un trajet entre deux points pendant une certaine durée en voyageant à vitesse fixe ou variable. Si le trajet prend un temps $$T$$, alors le paramètre t représente un instant dans $$T$$ qui se traduit par une position (point) sur la courbe.
Étant donnés un chemin droit (segment de ligne) entre les deux points $$A$$ et $$B$$, et un vecteur $$\mathbf{\vec v}$$ allant de $$A$$ à $$B$$ ( $$\mathbf{\vec v} = B - A$$), alors vous pouvez utiliser l’équation de ligne paramétrique pour trouver tous les points $$M$$ situés entre $$A$$ et $$B$$ de cette façon :
$$M = A + t*(B-A)$$
Où :
$$t$$ est une valeur comprise entre 0 et 1.
La gamme de valeurs t, de 0 à 1 dans ce cas, est appelée le domaine de la courbe ou intervalle. Si t est une valeur en dehors du domaine (inférieure à 0 ou supérieure à 1), le point $$M$$ se trouvera en dehors de la courbe linéaire $$\overline{AB}$$.
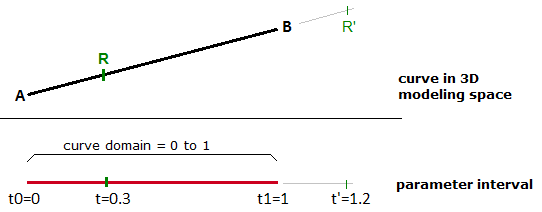
Le même principe s’applique à toute courbe paramétrique. Tout point sur la courbe peut être calculé en utilisant le paramètre t dans les limites de l’intervalle ou du domaine des valeurs qui définissent les limites de la courbe. Le paramètre de départ du domaine est normalement appelé $$t0$$ et la fin du domaine $$t1$$.
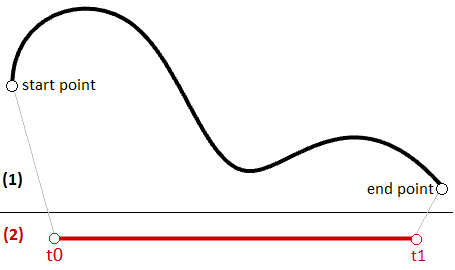
Domaine ou intervalle de la courbe
Le domaine ou intervalle de la courbe est défini comme la gamme de paramètres qui donnent un point sur cette courbe. Le domaine est normalement représenté par deux nombres réels définissant les limites du domaine exprimées sous la forme (min à max) ou (min, max). Les limites du domaine peuvent être deux valeurs quelconques qui peuvent ou non être corrélées à la longueur de la courbe. Dans un domaine croissant, le paramètre min du domaine détermine le point de départ de la courbe et le max détermine le point final de la courbe.
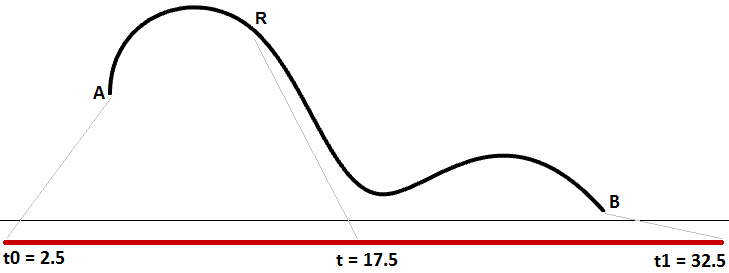
La modification du domaine d’une courbe correspond au processus de reparamétrisation de la courbe. Par exemple, le domaine d’une courbe est souvent modifié pour devenir (0, 1). La reparamétrisation d’une courbe ne modifie pas la forme de la courbe 3D. Cela revient à modifier le temps de trajet sur un chemin, en courant au lieu de marcher, ce qui ne change pas la forme du chemin.
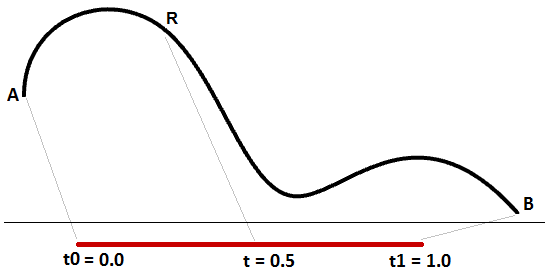
Un domaine croissant signifie que la valeur minimum du domaine pointe vers le début de la courbe. Les domaines sont normalement croissants, mais pas toujours.
Évaluation d’une courbe
Nous avons appris que l’intervalle d’une courbe est la gamme de toutes les valeurs de paramètre qui définissent des points sur la courbe 3D. Toutefois, rien ne garantit que l’évaluation au milieu du domaine, par exemple, donnera un point se trouvant au milieu de la courbe, comme le montre la Figure (29).
La paramétrisation uniforme d’une courbe peut être vue comme un trajet à vitesse constante le long d’un chemin. Une ligne de degré 1 entre deux points est un exemple où des intervalles de paramètres égaux se traduisent par des intervalles de même longueur d’arc sur la ligne. Il s’agit d’un cas particulier où des intervalles égaux de paramètres se traduisent par des intervalles de même longueur sur la courbe 3D.
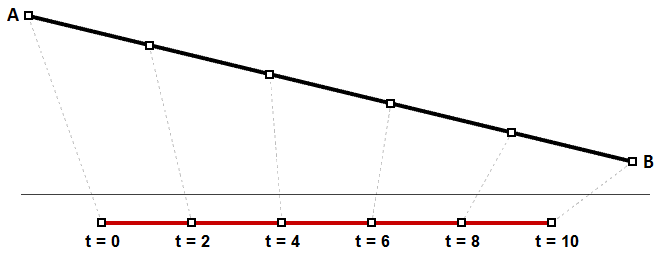
Il est toutefois beaucoup plus probable que la vitesse augmente ou diminue le long du trajet. Par exemple, si un trajet prend 30 minutes, il est peu probable que vous vous trouviez pile à mi chemin après 15 minutes. La Figure (30) montre un cas typique où des intervalles égaux de paramètres se traduisent par des segments de différentes longueurs sur la courbe 3D.
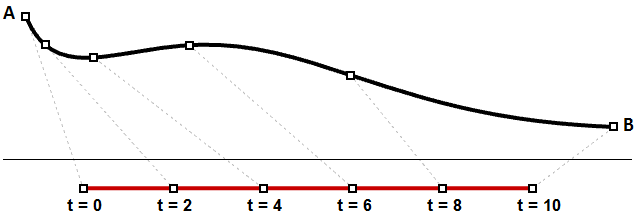
Vous devrez sûrement analyser les points se trouvant à un certain pourcentage de la longueur totale sur la courbe 3D. Par exemple, vous devrez peut-être diviser la courbe en segments de même longueur. Les logiciels de modélisation 3D possèdent normalement les outils permettant d’analyser des courbes en fonction des longueurs d’arc.
Vecteur tangent à une courbe
La tangente d’une courbe en tout paramètre (ou point sur la courbe) est le vecteur touchant la courbe en ce point mais ne la traversant pas. La pente du vecteur tangent correspond à la pente de la courbe en ce même point. L’exemple suivant détermine la tangente à une courbe au niveau de deux paramètres distincts.
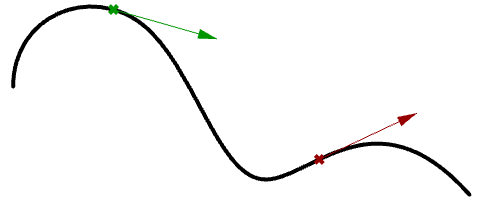
Courbes polynomiales cubiques
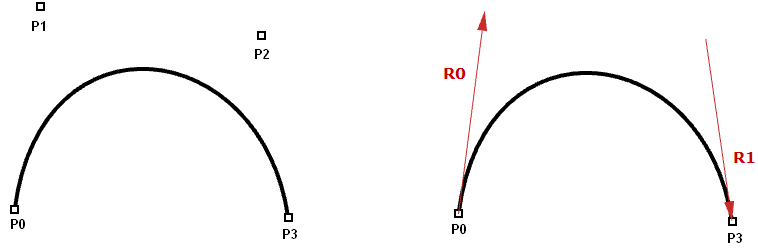
Les courbes d’Hermite et Bézier sont deux exemples de courbes polynomiales cubiques définies par quatre paramètres. Une courbe d’Hermite est définie par deux extrémités et deux vecteurs tangents au niveau de celles-ci, alors qu’une courbe de Bézier est définie par quatre points. Même si leur définition mathématique n’est pas la même, elles partagent des caractéristiques et limites similaires.
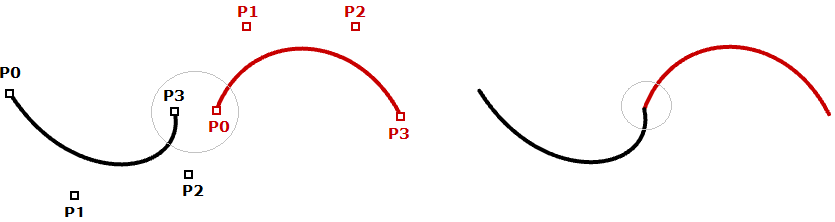
Dans la plupart des cas, les courbes sont composées de plusieurs segments. Cette particularité demande de créer une courbe cubique par morceaux. L’illustration suivante montre une courbe de Bézier par morceaux qui utilise 7 points pour créer une courbe cubique de deux segments. Vous remarquerez que même si la courbe finale est jointe, elle n’est ni lisse ni continue.
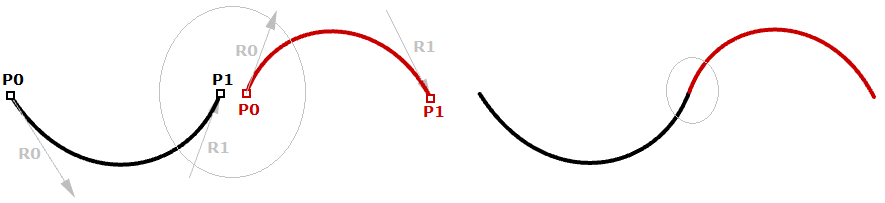
Même si les courbes d’Hermite utilisent le même nombre de paramètres que les courbes de Bézier (quatre paramètres pour définir une courbe), elles donnent des informations supplémentaires sur la courbe tangente qui peut également être partagée avec le morceau suivant afin de créer une courbe plus lisse avec un plus petit nombre de points, comme le montre l’illustration suivante.
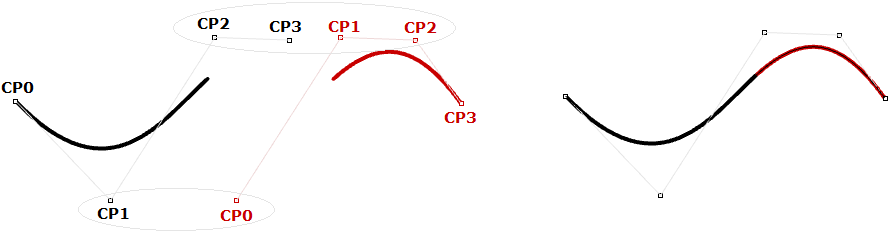
Les représentations de courbes utilisant des B-spline rationnelles non uniformes (NURBS) sont très robustes et conservent des éléments encore plus lisses et plus continus. Les segments partagent davantage de points de contrôle afin d’obtenir des courbes encore plus lisses en utilisant moins d’espace de mémoire.
Les courbes et surfaces NURBS sont les principales représentations mathématiques utilisées par Rhino pour dessiner la géométrie. Les caractéristiques et composants des courbes NURBS seront expliqués plus en détails dans ce chapitre.
Calcul des courbes de Bézier cubiques
L’algorithme de Casteljau, dont le nom provient de son inventeur Paul de Casteljau, calcule des courbes de Bézier à l’aide d’une méthode récursive. Les étapes de l’algorithme peuvent être résumées ainsi :
Données de départ :
Quatre points $$A$$, $$B$$, $$C$$, $$D$$ définissent une courbe ; $$t$$ est un paramètre dans le domaine de la courbe.
Résultat :
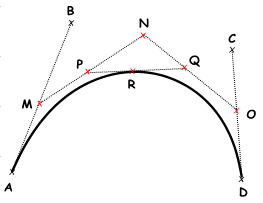
Point $$R$$ sur le courbe correspondant au paramètre $$t$$.
Solution :
- Trouver le point
$$M$$ correspondant au paramètre
$$t$$ sur la ligne
$$\overline{AB}$$.
2.Trouver le point $$N$$ correspondant au paramètre $$t$$ sur la ligne $$\overline{BC}$$.
3.Trouver le point $$O$$ correspondant au paramètre $$t$$ sur la ligne $$\overline{CD}$$.
4.Trouver le point $$P$$ correspondant au paramètre $$t$$ sur la ligne $$\overline{MN}$$.
5.Trouver le point $$Q$$ correspondant au paramètre $$t$$ sur la ligne $$\overline{NO}$$.
6.Trouver le point $$R$$ correspondant au paramètre $$t$$ sur la ligne $$\overline{PQ}$$.
3.2 Courbes NURBS
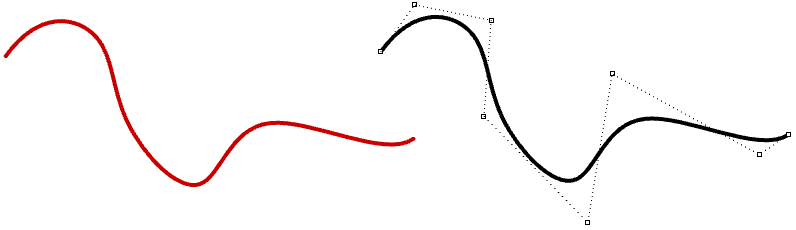
Les NURBS sont des représentations mathématiques précises de courbes dont la modification est très intuitive. Il est facile de représenter des courbes de forme libre à l’aide de NURBS et la structure de contrôle permet une édition facile et prévisible.
Il existe de nombreux livres et documents de référence si vous souhaitez des informations plus approfondies sur les NURBS. Une compréhension de base des NURBS est toutefois nécessaire pour utiliser plus efficacement un modeleur NURBS. Quatre attributs principaux définissent une courbe NURBS : le degré, les points de contrôle, les nœuds et les règles d’évaluation.
- Wikipedia : algorithme de De Boor
- Université technique du Michigan, Faculté de sciences de l’informatique, algorithme de De Boor
Degré
Le degré d’une courbe est un nombre positif entier. Rhino permet de travailler avec toutes les courbes, quel que soit leur degré, en commençant à 1. Les degrés 1, 2, 3 et 5 sont les plus couramment utilisés alors que le degré 4 et ceux supérieurs à 5 ne sont pas beaucoup utilisés dans le monde réel. Voici quelques exemples de courbes avec leur degré :
| Les lignes et polylignes sont des courbes NURBS de degré 1. |  |
| Les cercles et les ellipses sont des courbes NURBS de degré 2. |  |
| Les courbes de forme libre sont normalement représentées sous forme de courbes NURBS de degré 3 ou 5. |
 |
Points de contrôle
Les points de contrôle d’une courbe NURBS sont une liste d’au moins (degré + 1) points. Une des façons les plus intuitives de changer la forme d’une courbe NURBS est de déplacer ses points de contrôle.
Le nombre de points de contrôle jouant sur chaque segment d’une courbe NURBS est défini par le degré de la courbe. Par exemple, chaque segment d’une courbe de degré 1 est affecté uniquement par deux points de contrôle (extrémités). Pour les courbes de degré 2, chaque segment est affecté par trois points de contrôle et ainsi de suite.
| Les courbes de degré 1 passent par tous leurs points de contrôle. Dans une courbe NURB de degré 1, deux (degré + 1) points de contrôle définissent chaque segment. Si la courbe possède cinq points de contrôle, elle est composée de quatre segments. | 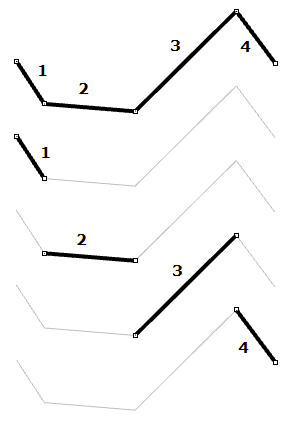 |
| Les cercles et les ellipses sont des exemples de courbes de degré 2. Dans une courbe NURBS de degré 2, trois (degré + 1) points de contrôle définissent chaque segment. Si la courbe possède cinq points de contrôle, elle est composée de trois segments. | 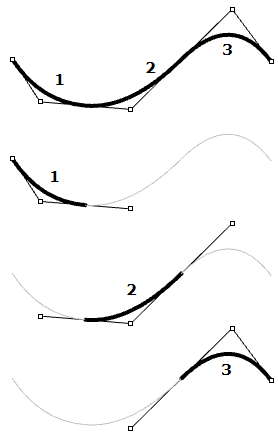 |
| Les points de contrôle des courbes de degré 3 ne touchent normalement pas la courbe, sauf ceux situés aux extrémités des courbes ouvertes. Dans une courbe NURBS de degré 3, quatre (degré + 1) points de contrôle définissent chaque segment. Si la courbe possède cinq points de contrôle, elle est composée de deux segments | 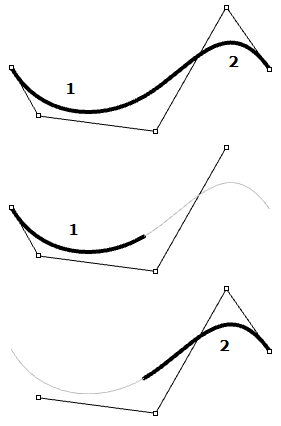 |
Poids des points de contrôle
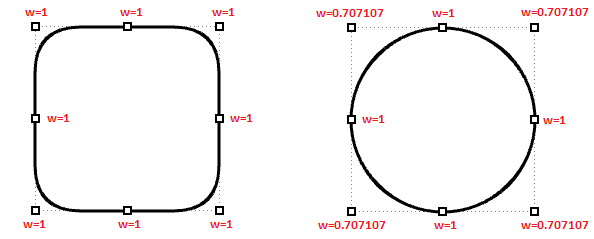
Un nombre, appelé poids, est associé à chaque point de contrôle. Sauf dans quelques exceptions, les poids ont des valeurs positives. Si tous les points de contrôle ont le même poids, normalement 1, la courbe est appelée non-rationnelle. Intuitivement, vous pouvez considérer les poids comme la quantité de gravité que possède chaque point de contrôle. Plus le poids relatif d’un point de contrôle est élevé, plus la courbe est attirée vers ce point de contrôle.
Il convient de remarquer qu’il est plus prudent de ne pas modifier le poids des points. La modification des poids ne donne que rarement le résultat désiré tout en entraînant de nombreux problèmes de calcul dans certaines opérations comme les intersections. La seule bonne raison d’utiliser les courbes rationnelles est de représenter des courbes qui ne peuvent pas être dessinées d’une autre façon, comme les cercles et les ellipses.
Nœuds
Chaque courbe NURBS possède une liste de nombres associés que nous appelons une liste de nœuds (parfois également appelés vecteur nodal). Il est un peu plus difficile de comprendre la notion de nœuds et de les définir. Lorsque vous utilisez un modeleur 3D, vous n’aurez pas besoin de définir manuellement les nœuds de chaque courbe que vous créez ; mais il vous sera utile de comprendre quelques informations sur les nœuds.
Les nœuds sont des valeurs de paramètre
Les nœuds correspondent à une liste non décroissante de valeurs de paramètres comprises dans le domaine de la courbe. Dans Rhino, le nombre de nœuds est égal au nombre de points de contrôle plus le degré -1. C’est-à-dire que le nombre de nœuds est égal au nombre de points de contrôle plus le degré de la courbe moins 1 :
|nœuds| = |points de contrôle| + Degré - 1
Normalement, pour les courbes périodiques de degré n, les n premiers nœuds correspondent à la valeur minimum du domaine alors que les n derniers nœuds correspondent à la valeur maximum du domaine.
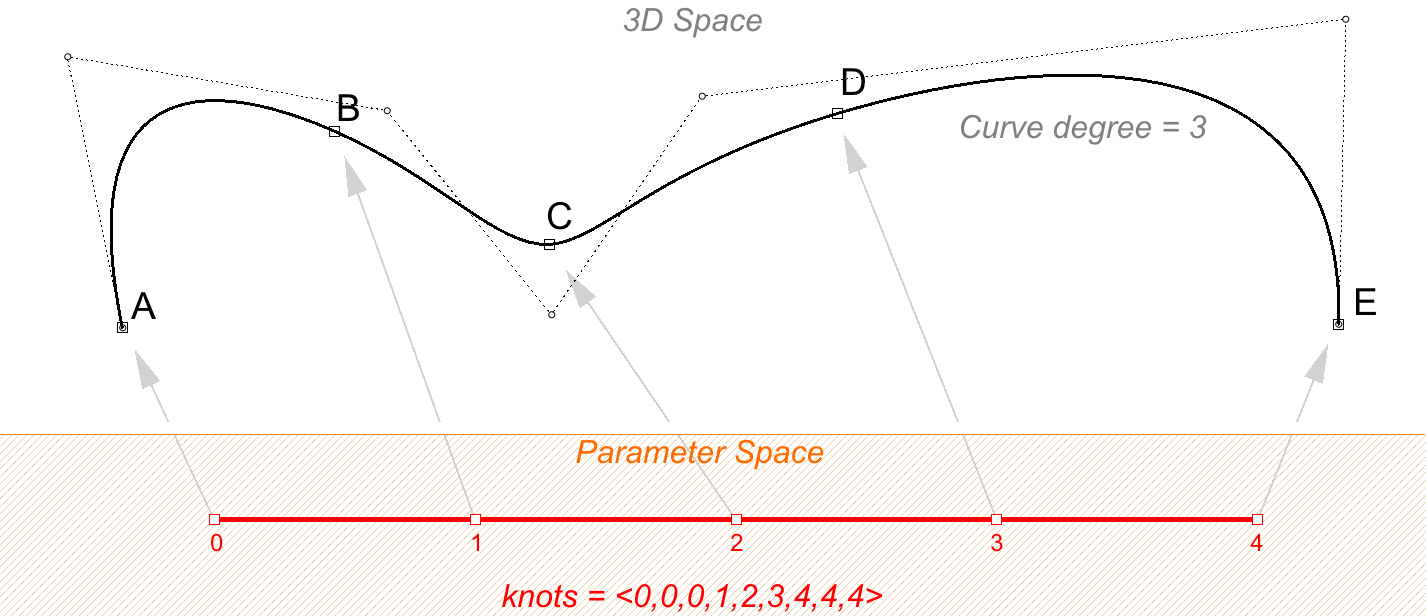
Par exemple, les nœuds d’une courbe NURBS de degré 3 avec 7 points de contrôle dont le domaine se trouve entre 0 et 4 sont de type <0, 0, 0, 1, 2, 3, 4, 4, 4>.
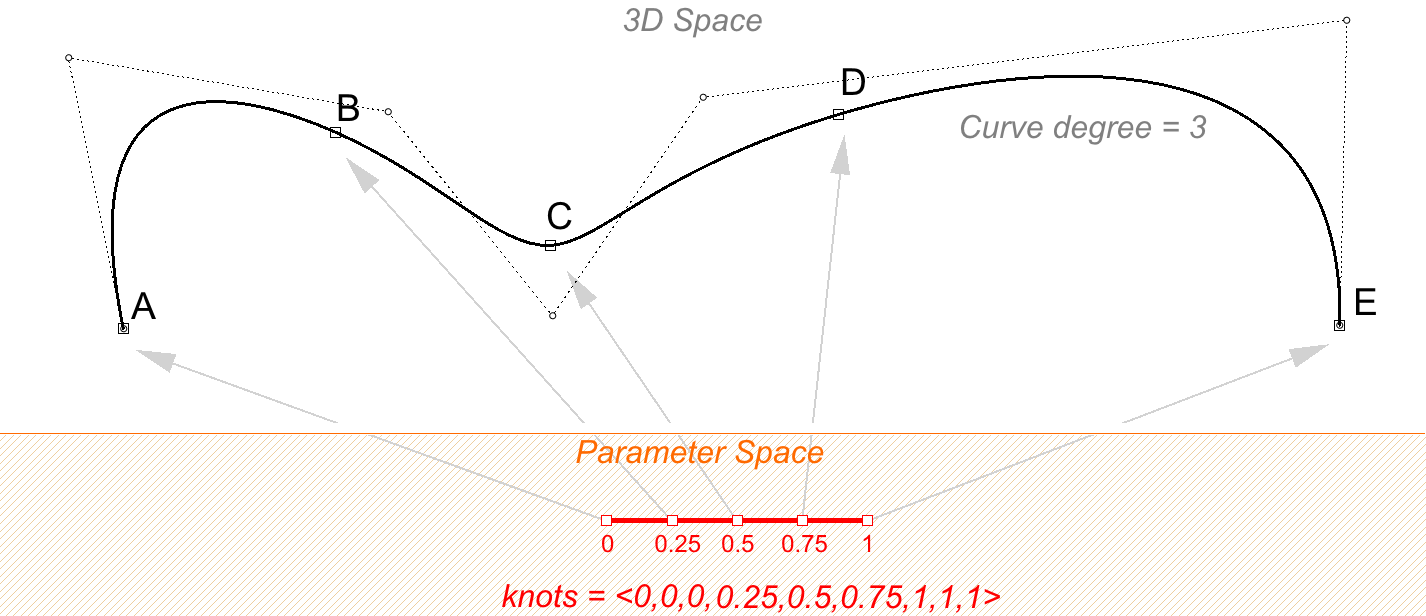
Si l’échelle d’une liste de nœuds est modifiée sur une courbe, la courbe 3D n’est pas modifiée. Si vous modifiez le domaine de la courbe dans l’exemple précédent de “0 à 4” en “0 à 1”, l’échelle de la liste des nœuds est changée mais la courbe 3D quant à elle n’est pas modifiée.
Un nœud dont la valeur n’apparaît qu’une seule fois est appelé un nœud simple. Les nœuds intérieurs sont en principe des nœuds simples comme dans les deux exemples précédents.
Multiplicité de nœud
La multiplicité d’un nœud est le nombre de fois qu’il apparaît dans la liste de nœuds. Elle ne peut pas être supérieure au degré de la courbe. Cette valeur est utilisée pour contrôler la continuité de la courbe au niveau du point correspondant.
Nœuds de multiplicité maximale
La multiplicité maximale d’un nœud est égale au degré de la courbe. Au niveau de chaque nœud de multiplicité maximale il existe un point de contrôle par lequel passe la courbe.
Par exemple, les courbes ouvertes ou vissées aux extrémités possèdent des nœuds de multiplicité maximale à leurs extrémités. C’est pour cette raison que les points de contrôle extrêmes coïncident avec les extrémités de la courbe. Les nœuds intérieurs de multiplicité maximale créent un point de rebroussement.
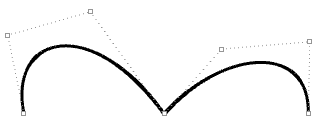
Par exemple, les courbes suivantes sont toutes deux de degré 3 et possèdent le même nombre de points de contrôle, dans la même position. Cependant, leurs nœuds sont différents et leur forme également. La multiplicité maximale force la courbe à passer par le point de contrôle correspondant.
Voici deux courbes qui ont le même degré, le même nombre et le même emplacement de points de contrôle, mais dont le vecteur de nœuds est différent, ce qui se traduit par une forme de courbe différente :
| Degré = 3 Nombre de points de contrôle = 7 Nœuds = <0,0,0,1,2,3,4,4,4> = 9 nœuds Domaine (0 à 4) |
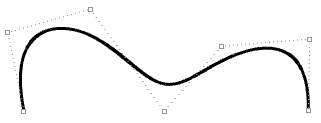 |
| Degré = 3 Nombre de points de contrôle = 7 Nœuds = <0,0,0,1,1,1,4,4,4> = 9 nœuds Domaine (0 à 4) Remarque : un nœud de multiplicité maximale au milieu crée un point de rebroussement et la courbe passe alors forcément par le point de contrôle correspondant. |
 |
Nœuds uniformes
Une liste uniforme de nœuds répond à la condition suivante.
La liste de nœuds commence par un nœud de multiplicité maximale suivi de nœuds simples et se termine par un nœud de multiplicité maximale. Les valeurs sont croissantes et l’intervalle entre elles est régulier. Cette disposition est typique des les courbes vissées aux extrémités ou ouvertes. Les courbes périodiques fonctionnent différemment comme nous le verrons par la suite.
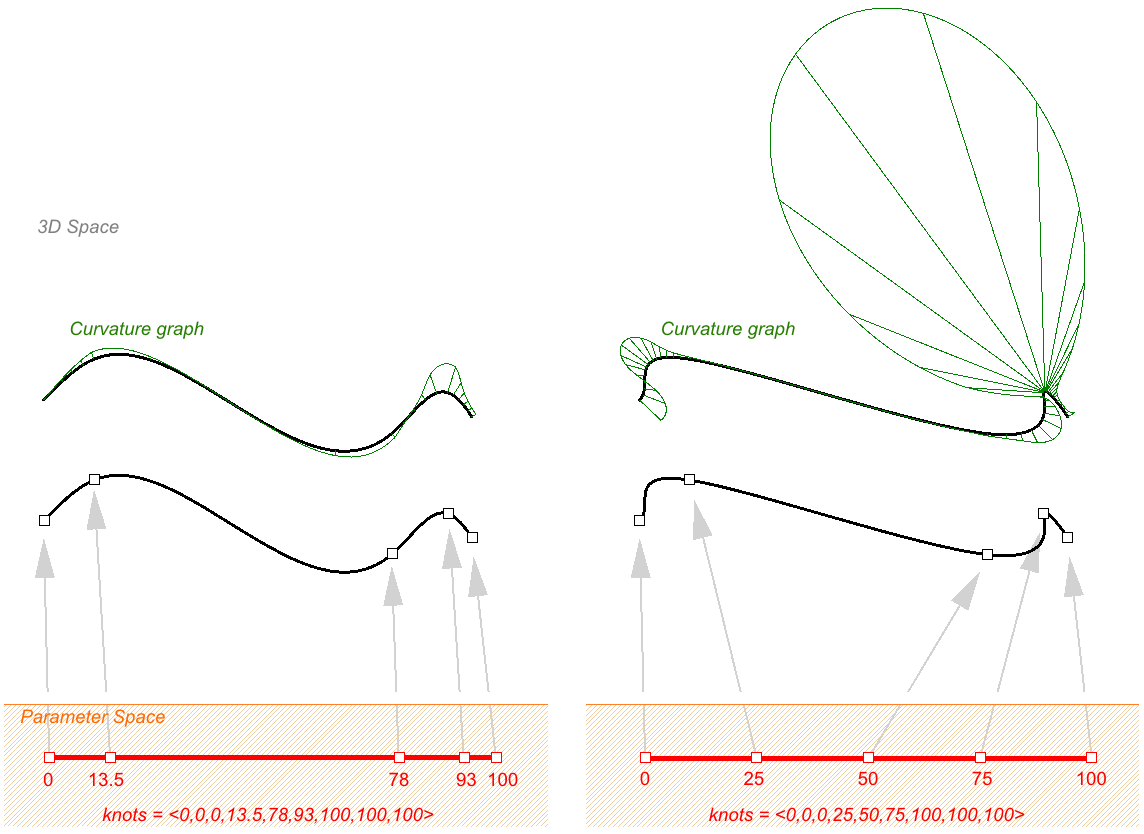
Nœuds non uniformes
Les courbes NURBS peuvent présenter des espaces irréguliers entre les nœuds, afin d’aider à contrôler la courbure le long de la courbe et de créer des courbes plus lisses. Prenons l’exemple suivant présentant une interpolation de points avec une liste de nœuds non uniforme à gauche et une liste uniforme à droite. Par définition, si l’espacement des nœuds sur une courbe NURBS est proportionnel à l’espacement entre les points de contrôle, la courbe est alors plus lisse.
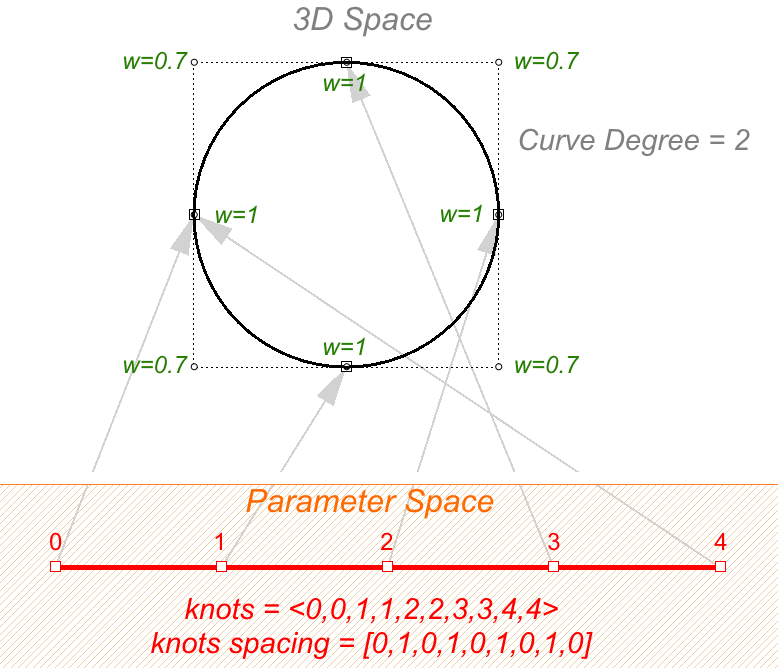
Un exemple de courbe non uniforme et rationnelle, le cercle NURBS. L’exemple suivant montre une courbe de degré 2 avec 9 points de contrôle et 10 nœuds. Le domaine est de 0-4 et l’espacement alterne entre 0 et 1. nœuds = <0,0,1,1,2,2,3,3,4,4> — (multiplicité maximale dans les nœuds intérieurs) espacement entre les nœuds = [0,1,0,1,0,1,0,1,0] — (non uniforme)
Règle d’évaluation
La règle d’évaluation utilise une formule mathématique qui prend un nombre dans le domaine de la courbe et assigne un point. La formule prend en considération le degré, les points de contrôle et les nœuds.
En utilisant cette formule, les fonctions spécialisées peuvent prendre un paramètre de la courbe et produire le point correspondant sur cette courbe. Un paramètre est un nombre faisant partie du domaine de la courbe. Les domaines sont normalement croissants et composés de deux nombres : le paramètre minimum du domaine $$t(0)$$ qui donne le point de départ de la courbe et le maximum $$t(1)$$ qui donne le point final de la courbe.
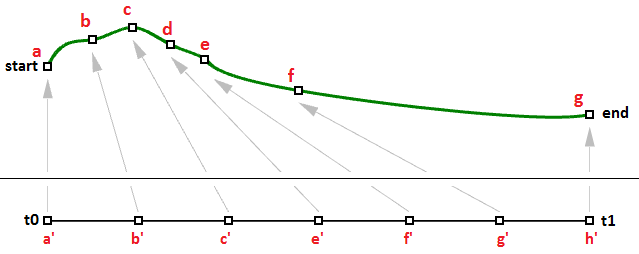
Caractéristiques des courbes NURBS
Afin de créer une courbe NURBS, nous aurons besoin des informations suivantes :
- Espace dimensionnel, normalement 3
- Degré, (on utilise parfois l’ordre, qui est égal au degré+1)
- Points de contrôle (liste de points)
- Poids de chaque point de contrôle (liste de nombres)
- Nœuds (liste de nombres)
Lorsque vous créez une courbe, vous devez définir au moins le degré et la position des points de contrôle. Toutes les autres informations nécessaires à la construction des courbes NURBS peuvent être calculées automatiquement. Si le point final est identique au point de départ, la courbe créée sera fermée, lisse et périodique. Le tableau suivant montre des exemples de courbes ouvertes et fermées :
| Courbe ouverte de degré 1. La courbe passe par tous les points de contrôle. |
 |
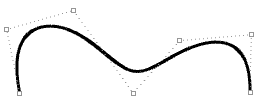
| Courbe ouverte de degré 3. Les deux extrémités de la courbe coïncident avec les points de contrôle des extrémités. |
 |
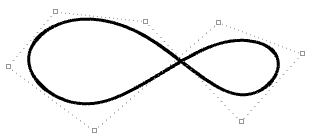
| Courbe périodique fermée de degré 3. La jointure de la courbe ne passe pas par un point de contrôle. |
 |
| Déplacer des points de contrôle sur une courbe périodique ne modifie pas son lissage. | 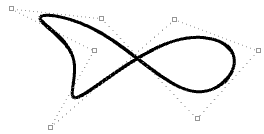 |
| Des points de rebroussement sont créés lorsqu’on force la courbe à passer par certains points de contrôle. | 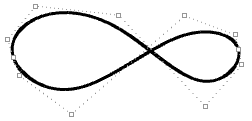 |
| Lorsque les points de contrôle d’une courbe non périodique sont déplacés, la continuité lisse de la courbe n’est plus garantie mais il est plus facile de contrôler le résultat. | 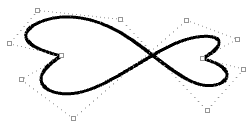 |
Courbes NURBS périodiques et courbes NURBS vissées aux extrémités
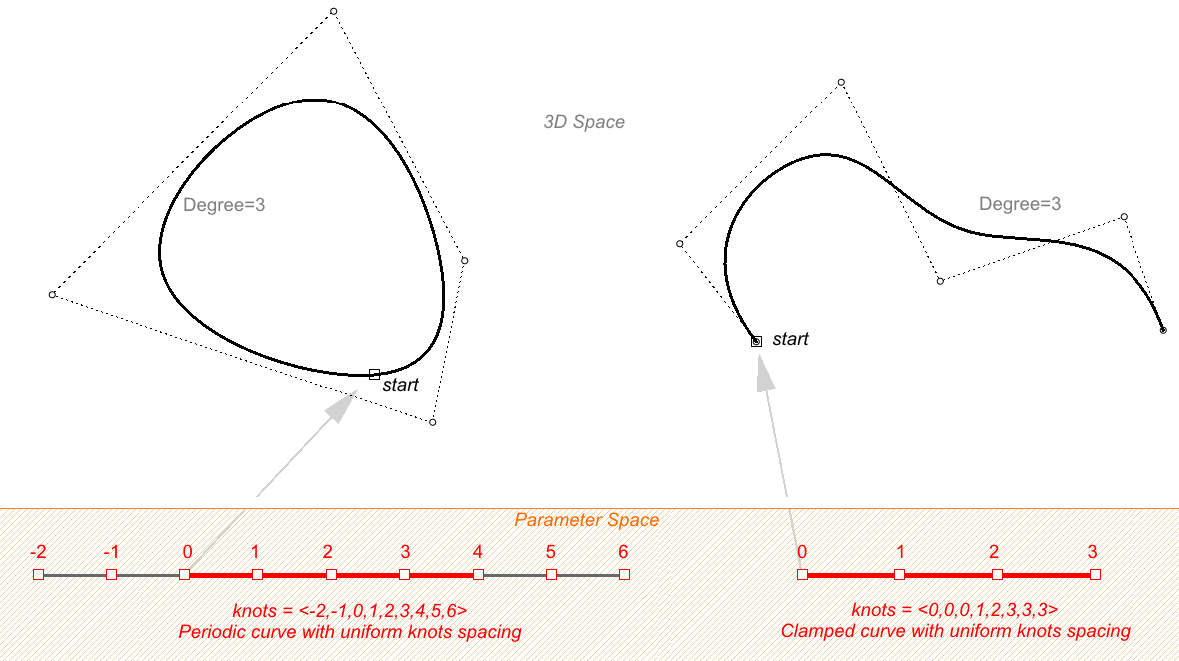
Les extrémités des courbes fermées vissées aux extrémités coïncident avec le premier et le dernier points de contrôle. Les courbes périodiques sont des courbes fermées lisses. La meilleure façon de comprendre les différences entre les deux est de comparer les points de contrôle et les nœuds.
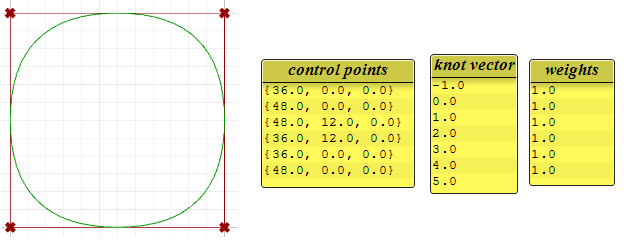
L’exemple ci-dessous montre une courbe NURBS non rationnelle ouverte vissée aux extrémités. Cette courbe possède quatre points de contrôle dont le poids est égal à 1 et des nœuds uniformes dont les deux extrêmes sont de multiplicité maximale.

La courbe circulaire ci-dessous est une courbe NURBS périodique fermée de degré 3. Elle est également non rationnelle car tous les poids sont égaux. Vous remarquerez que les courbes non périodiques ont besoin d’un plus grand nombre de points de contrôle et présentent moins de superposition. Les nœuds sont des nœuds simples.
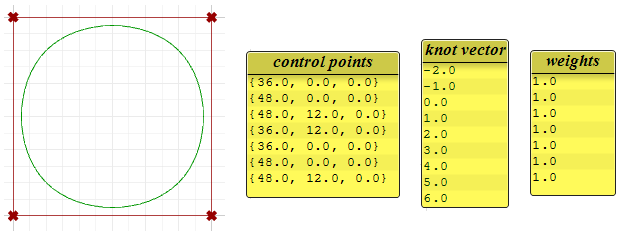
Vous remarquerez que la courbe périodique a converti les quatre points de départ en sept points de contrôle (degré + 4), alors que la courbe vissée aux extrémités n’utilisait que les quatre points de contrôle. Les courbes périodiques utilisent uniquement des nœuds simples alors que les nœuds au début et à la fin des courbes vissées aux extrémités sont de multiplicité maximale, ce qui force la courbe à passer par le premier et le dernier points de contrôle.
Si nous définissons le degré des exemples précédentes sur 2 au lieu de 3, les nœuds deviennent plus petits et le nombre de points de contrôle des courbes périodiques change.
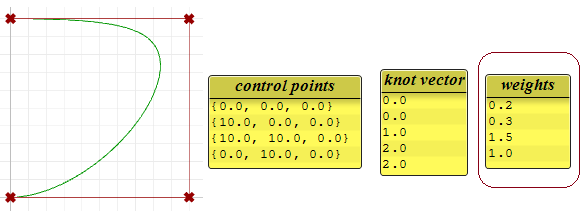
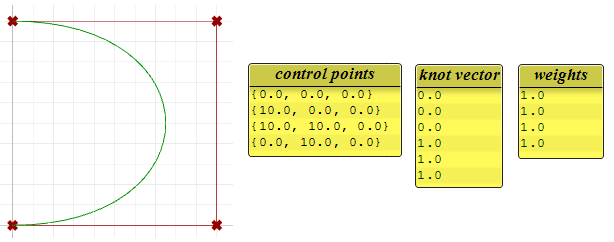
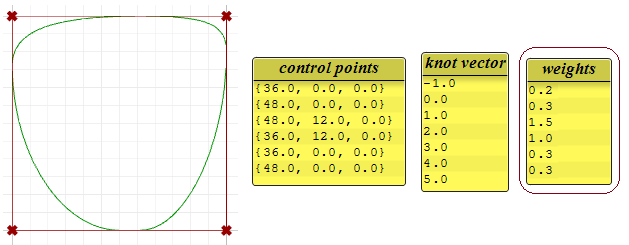
Poids
Les poids des points de contrôle d’une courbe NURBS uniforme sont égaux à 1, mais ce nombre peut varier pour les courbes NURBS rationnelles. L’exemple suivant montre l’effet produit par la variation des points de contrôle.
Calcul des courbes NURBS
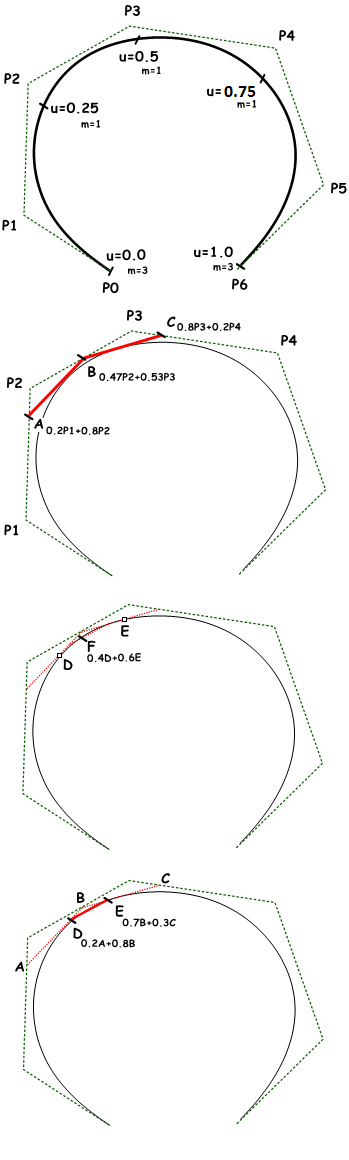
L’algorithme de De Boor, de son inventeur Carl de Boor, est une généralisation de l’algorithme de Casteljau pour les courbes de Bézier. Il est numériquement stable et largement utilisé pour calculer les points sur des courbes NURBS dans les applications 3D. L’exemple suivant calcule un point sur une courbe NURBS de degré 3 à l’aide de l’algorithme de De Boor.
Données de départ :
Sept points de contrôle
$$P0$$ à
$$P6$$
Nœuds :
$$u_0 = 0.0$$
$$u_1 = 0.0$$
$$u_2 = 0.0$$
$$u_3= 0.25$$
$$u_4 = 0.5$$
$$u_5 = 0.75$$
$$u_6 = 1.0$$
$$u_7 = 1.0$$
$$u_8 = 1.0$$
Résultat :
Point sur la courbe correspondant à $$u=0.4$$
Solution :
1. Calculer les coefficients pour définir la première itération :
$$A_c = ((u – u_1)/(u_{1+3} – u_1) = 0.8$$
$$B_c = (u – u_2)/(u_{2+3} – u_2) = 0.53$$
$$C_c = (u – u_3)/(u_{3+3} – u_3) = 0.2$$
2. Calculer les points en utilisant les données des coefficients :
$$A = 0.2P_1 + 0.8P_2$$
$$B = 0.47 P_2 + 0.53 P_3$$
$$C = 0.8 P_3 + 0.2 P_4$$
3. Calculer les coefficients pour la deuxième itération :
$$D_c = (u – u_2) / (u_{2+3-1} – u_2) = 0.8$$
$$E_c = (u – u_3) / (u_{3+3-1} – u_3) = 0.3$$
4. Calculer les points en utilisant les données des coefficients :
$$D = 0.2A+ 0.8B$$
$$E = 0.7B + 0.3C$$
5. Calculer le dernier coefficient :
$$Fc = (u – u_3)/ (u_{3+3-2} – u_3) = 0.6$$
Trouver le point sur la courbe correspondant au paramètre $$u=0.4$$ :
$$F= 0.4D + 0.6E$$
3.3 Continuité géométrique d’une courbe
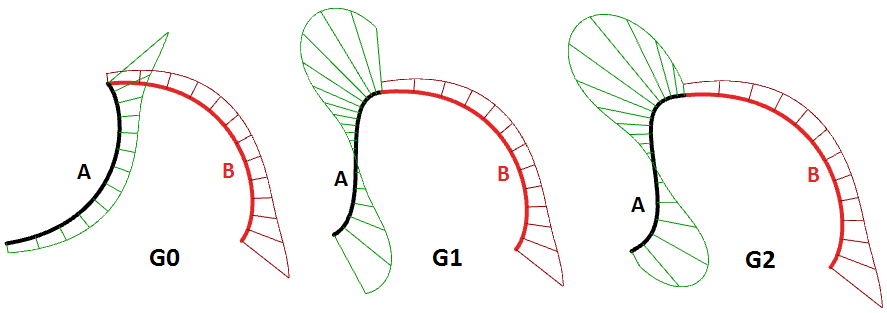
La continuité est un concept important en modélisation 3‑D. La continuité est essentielle pour l’aspect lisse, la réflexion de la lumière et les flux d’air. Le tableau suivant montre différentes continuités et leurs définitions :
| G0| (Position continue) | Deux segments de courbe joints |
| G1| (Continuité de tangence) | La direction de la tangente au point de jonction est la même pour les deux segments de courbe. |
| G2| (Continuité de courbure) | Les courbures ainsi que les tangentes sont les mêmes pour les deux segments de courbe au niveau de leur point commun. |
| GN|……. | Les courbes coïncident à un ordre plus élevé|
3.4 Courbure de la courbe
La courbure est un concept largement utilisé dans la modélisation de courbes et surfaces 3‑D. La courbure est définie comme le changement d’inclinaison de la tangente d’une courbe sur une unité de longueur d’arc. Pour un cercle ou une sphère, la courbure correspond à l’inverse du rayon et elle est constante sur tout le domaine.
En tout point d’une courbe dans un plan, la ligne se rapprochant le plus de la courbe qui passe par ce point est la ligne tangente. Nous pouvons aussi rechercher le cercle passant par ce point, se rapprochant le plus de la courbe et tangent à celle-ci. L’inverse du rayon de ce cercle est la courbure de la courbe en ce point.
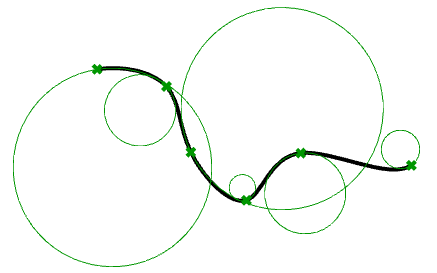
Le cercle se rapprochant le plus de la courbe peut se trouver à gauche ou à droite de celle-ci. Si cette information est importante pour nous, nous pouvons définir une règle, telle que donner le signe positif à une courbure si le cercle se trouve à gauche et négatif si le cercle se trouve à droite de la courbe. Cette notion est appelée courbure signée. Les valeurs de courbure de courbes jointes indiquent une continuité entre ces courbes.
3.5 Surfaces paramétriques
Paramètres de surface
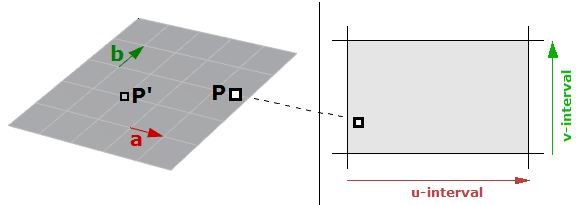
Une surface paramétrique est une fonction de deux paramètres indépendants (normalement notés $$u$$, $$v$$) sur un domaine en deux dimensions. Prenons pour exemple un plan. Soient un point $$P$$ sur le plan et deux vecteurs non parallèles sur le plan, $$\vec a$$ and $$\vec b$$, on peut alors définir une équation paramétrique du plan avec les deux paramètres $$u$$ et $$v$$ ainsi :
$$P = P’ + u * \mathbf{\vec a} + v * \mathbf{\vec b}$$Où :
$$P’$$ est un point connu sur le plan
$$\mathbf{\vec a}$$ est le premier vecteur sur le plan
$$\mathbf{\vec b}$$ est le premier vecteur sur le plan
$$u$$ est le premier paramètre
$$v$$ est le premier paramètre
Autre exemple, la sphère. L’équation cartésienne d’une sphère centrée sur l’origine de rayon $$R$$ est :
$$x^2 + y^2 + z^2 = R^2$$Ainsi, pour chaque point, il existe trois variables ( $$x$$, $$y$$, $$z$$), ce qui n’est pas utile pour définir une représentation paramétrique qui demande uniquement deux variables. Toutefois, dans le système de coordonnées sphérique, chaque point est déterminé à l’aide des trois valeurs :
$$r$$ : distance radiale entre le point et l’origine
$$θ$$ : angle avec l’axe des x dans le plan xy
$$ø$$ : angle avec l’axe des z et le point
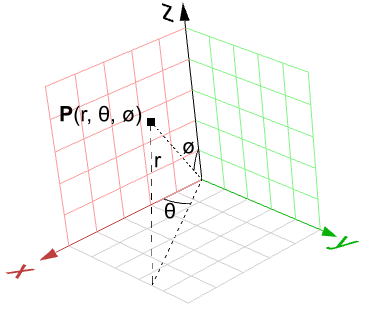
Il est possible de convertir des points depuis les coordonnées sphériques vers des coordonnées cartésiennes avec les formules suivantes :
$$x = r * sin(ø) * cos(θ)$$
$$y = r * sin(ø) * sin(θ)$$
$$z = r * cos (ø)$$
Où :
$$r$$ est la distance depuis l’origine
$$≥ 0$$
$$θ$$ va de
$$0$$ à
$$2π$$
$$ø$$ va de
$$0$$ à
$$π$$
Étant donné que $$r$$ est constant sur la surface d’une sphère, il ne reste que deux variables et on peut donc utiliser les informations précédentes pour créer la représentation paramétrique d’une surface sphérique :
$$u = θ$$
$$v = ø$$
De sorte que :
$$x = r * sin(v) * cos(u)$$
$$y = r * sin(v) * sin(u)$$
$$z = r * cos(v)$$
Où ( $$u$$, $$v$$) est dans le domaine ( $$2 π$$, $$π$$)
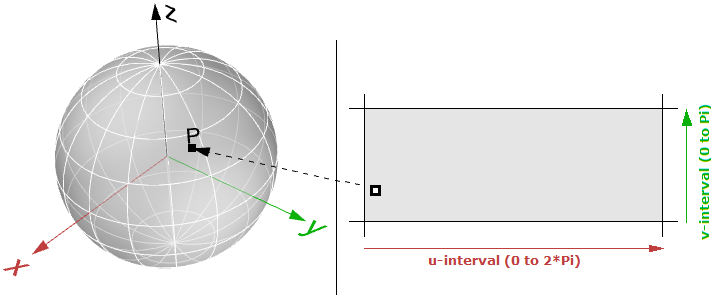
La surface paramétrique suit la forme générale :
$$x = x(u,v)$$
$$y = y(u,v)$$
$$z = z(u,v)$$
Où :
$$u$$ et $$v$$ sont deux paramètres compris dans la région ou le domaine de la surface.
Domaine de la surface
Le domaine d’une surface est défini comme la gamme de paramètres ( $$u,v$$) qui donnent un point 3D sur cette surface. Le domaine dans chaque dimension ( $$u$$ ou $$v$$) est normalement décrit par deux nombres réels ( $$u_{min}$$ à $$u_{max}$$) et ( $$v_{min}$$ à $$v_{max}$$)
La modification du domaine d’une surface correspond au processus de reparamétrisation de la surface. Un domaine croissant signifie que la valeur minimum du domaine pointe vers le point minimum de la surface. Les domaines sont normalement croissants, mais pas toujours.
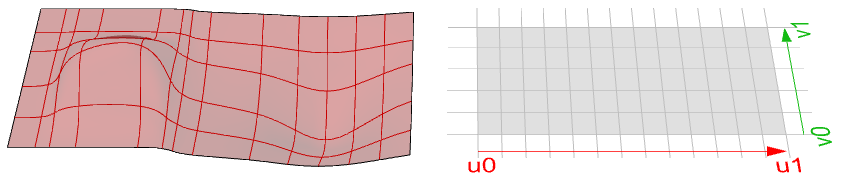
Calcul de surface
Le calcul d’une surface au niveau d’un paramètre se trouvant dans le domaine de la surface donne un point sur la surface. N’oubliez pas que le milieu du domaine ( $$u_{mid}$$, $$v_{mid}$$) ne correspond pas forcément au milieu de la surface 3D. Le calcul de valeurs $$u-$$ et $$v-$$ se trouvant en dehors du domaine de la surface ne donnera pas un résultat utile.
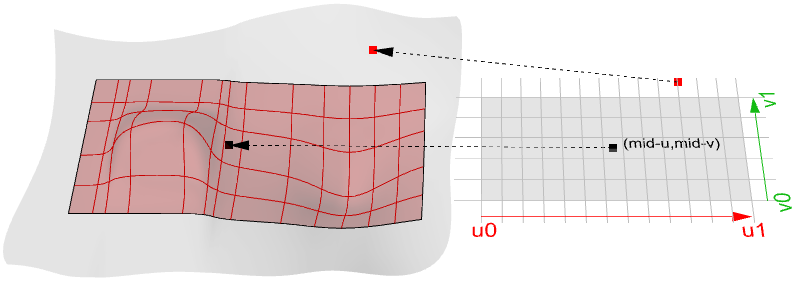
Plan tangent à une surface
Le plan tangent à une surface en un point donné est le plan qui touche la surface en ce point. La direction z du plan tangent représente la direction normale de la surface en ce point.
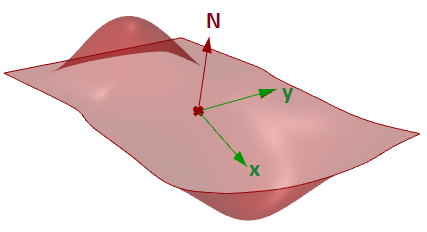
3.6 Continuité géométrique de surfaces
De nombreux modèles ne peuvent pas être construits à partir d’un patch de surface. La continuité entre des patchs de surface joints est importante pour l’aspect lisse, la réflexion de la lumière et les flux d’air. Le tableau suivant montre différentes continuités et leurs définitions :
| G0| (Position continue) | Deux surfaces jointes. |
| G1| (Continuité de tangence) | Les tangentes des deux surfaces le long de leur bord de jonction sont parallèles dans les directions u et v. |
| G2| (Continuité de courbure) | Les courbures ainsi que les tangentes sont les mêmes pour les deux surfaces au niveau de leur bord commun. |
| GN|……. | Les surfaces coïncident à un ordre plus élevé. |
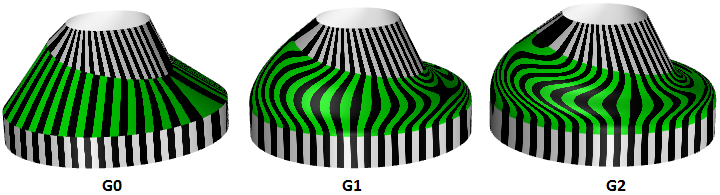
3.7 Courbure d’une surface
Pour les surfaces, la courbure normale est une généralisation de la courbure appliquée aux surfaces. Soit un point sur une surface et une direction reposant sur le plan tangent à la surface en ce point, la courbure de section normale est calculée en prenant l’intersection de la surface avec le plan défini par ce point, la normale de la surface en ce point et la direction. La courbure de section normale est la courbure positive ou négative de cette courbe au point en question.
Si on regarde dans toutes les directions dans le plan tangent à la surface au point en question et si on calcule la courbure de section normale dans toutes ces directions, on obtient une valeur maximale et une valeur minimale.
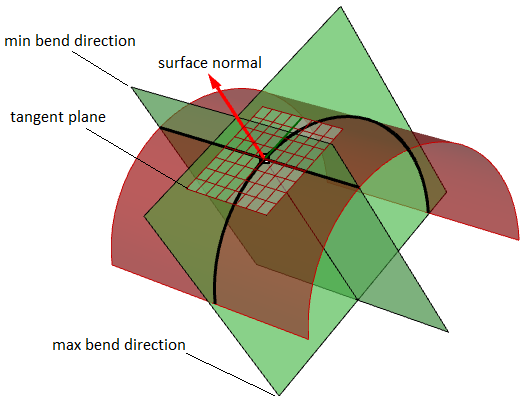
Courbures principales
Les courbures principales d’une surface en un point sont les valeurs minimale et maximale des courbures normales en ce point. Elles mesurent le gauchissement maximum et minimum de la surface en ce point. Les courbures principales sont utilisées pour calculer les courbures gaussienne et moyenne de la surface.
Par exemple, dans une surface cylindrique, la direction linéaire ne présente aucun gauchissement (courbure nulle) alors que le gauchissement est à son maximum au niveau de l’intersection avec un plan parallèle aux faces des extrémités (courbure = 1/rayon). Ces deux extrêmes constituent les courbures principales de cette surface.
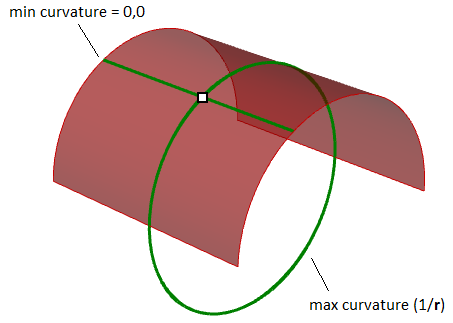
Courbure gaussienne
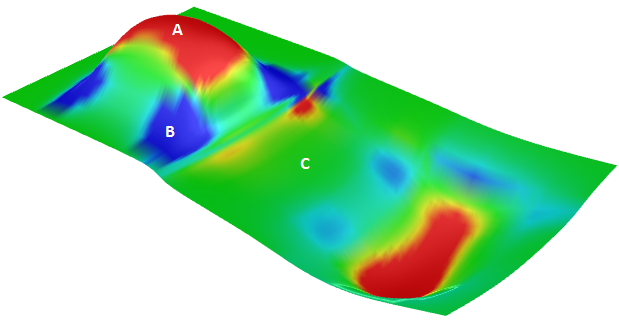
La courbure gaussienne d’une surface en un point est le produit des courbures principales en ce point. Le plan tangent de tout point dont la courbure gaussienne est positive touche la surface en un seul point, alors que le plan tangent de tout point dont la courbure gaussienne est négative coupe la surface.
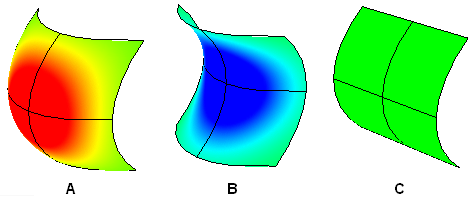
A : Courbure positive lorsque la surface est en forme de bol.
B : Courbure négative lorsque la surface est en forme de selle.
C : Courbure nulle lorsque la surface est plane dans au moins une direction (plan, cylindre).
Courbure moyenne
La courbure moyenne d’une surface en un point correspond à la moitié de la somme des courbures principales en ce point. Tout point dont la courbure moyenne est nulle présente une courbure gaussienne négative ou nulle.
Les surfaces dont la courbure moyenne est nulle en tout point sont des surfaces minimales. Les surfaces minimales peuvent être utilisées pour modéliser des procédés physiques tels que la formation de films de savon liés à des objets fixes comme des cercles de fils de fer. Un film de savon n’est pas déformé par la pression de l’air (qui est égale des deux côtés) et il est possible de minimiser son aire. Ce qui n’est pas le cas pour la bulle de savon, qui renferme une quantité fixe d’air et dont les pressions sont différentes à l’intérieur et à l’extérieur. La courbure moyenne est utile pour trouver des zones où la courbure de la surface change brusquement.
Les surfaces dont la courbure moyenne est constante en tout point sont souvent appelées surfaces à courbure moyenne constante (CMC). La formation de bulles liées à des objets ou libres est un exemple de surface CMC. Une bulle, à la différence d’un simple film, contient un volume et existe dans un équilibre où une pression un peu supérieure à l’intérieur de la bulle est compensée par les forces de surface minimale de la bulle elle-même.
3.8 Surfaces NURBS
Vous pouvez considérer les surfaces NURBS comme des grilles de courbes NURBS disposées selon deux directions. La forme d’une surface NURBS est définie par des points de contrôle et le degré de cette surface dans chacune des deux directions (u et v). Les surfaces NURBS sont très efficaces pour représenter des surfaces de forme libre avec un degré de précision très élevé. Les équations mathématiques et les détails des surfaces NURBS vont au-delà des données visées dans ce texte. Nous nous centrerons uniquement sur les caractéristiques les plus utiles pour les dessinateurs.
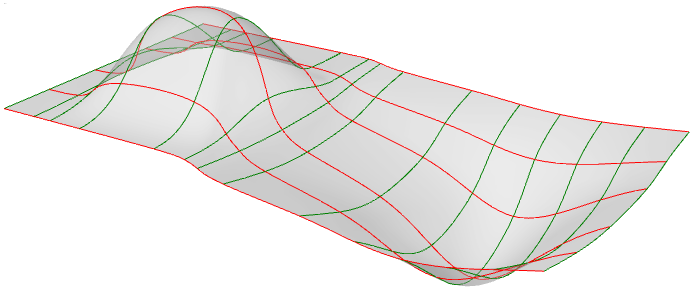
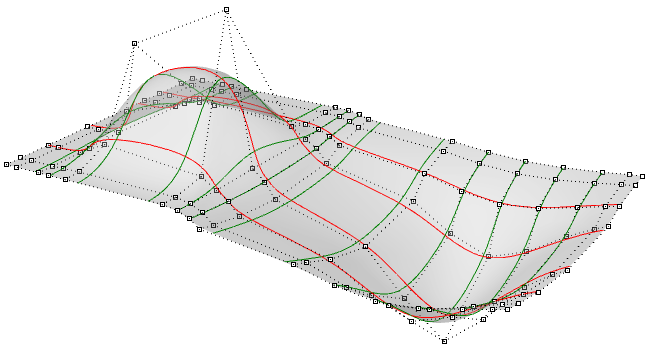
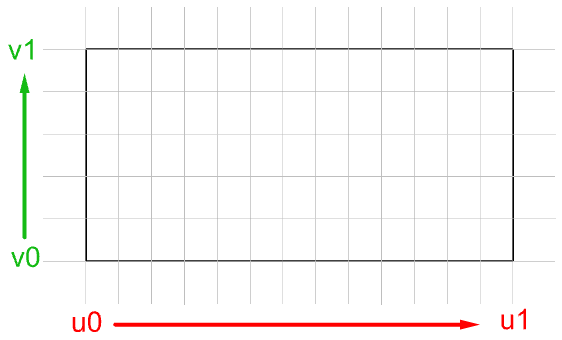
Dans la plupart des cas, le calcul de paramètres à intervalles réguliers dans un rectangle de paramètre 2D ne se traduit pas par des intervalles égaux dans l’espace 3D.
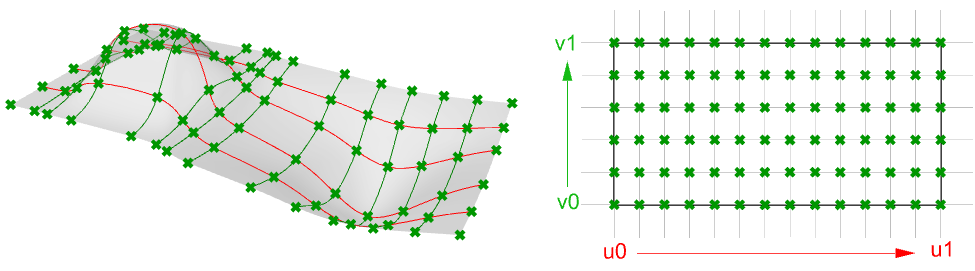
Caractéristiques des surfaces NURBS
Les caractéristiques des surfaces NURBS sont très proches de celles des courbes NURBS, sauf qu’il y a un paramètre supplémentaire. Les surfaces NURBS possèdent les informations suivantes :
- Espace dimensionnel, normalement 3
- Degré dans les directions u et v : (l’ordre, qui est égal au degré+1, est parfois utilisé)
- Points de contrôle (points)
- Poids des points de contrôle (nombres)
- Nœuds (nombres)
Comme pour les courbes NURBS, vous n’aurez probablement pas besoin de connaître tous les détails concernant la création des surfaces NURBS car les modeleurs 3D offrent de bons outils pour cela. Vous pouvez toujours reconstruire les surfaces (et les courbes si besoin) pour leur donner un autre degré et modifier leur nombre de points de contrôle. Une surface peut être ouverte, fermée ou périodique. Voici quelques exemples de surfaces :
| Surface de degré 1 dans les deux directions u et v. Tous les points de contrôle sont situés sur la surface. | 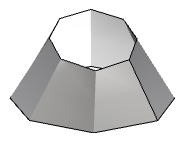 |
| Surface ouverte de degré 3 dans la direction u et de degré 1 dans la direction v. Les sommets de la surface coïncident avec les points de contrôle des sommets. | 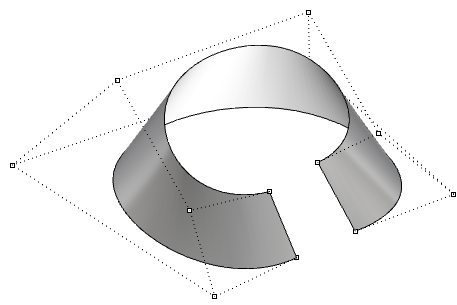 |
| Surface fermée (non périodique) de degré 3 dans la direction u et de degré 1 dans la direction v. Certains points de contrôle coïncident avec la jointure de la surface. | 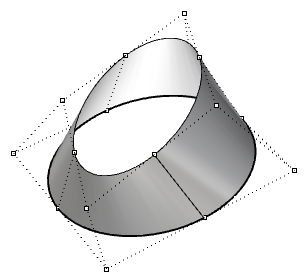 |
| Si les points de contrôle sont déplacés sur une surface fermée (non périodique), un point de rebroussement est créé et la surface n’est plus lisse. | 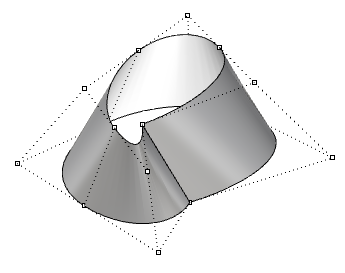 |
| Surface périodique de degré 3 dans la direction u et de degré 1 dans la direction v. Les points de contrôle de la surface ne coïncident pas avec la jointure de la surface. | 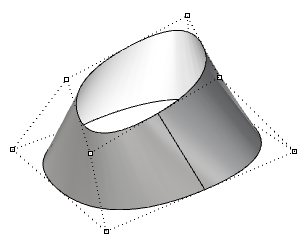 |
| Déplacer des points de contrôle sur une surface périodique ne modifie pas son lissage et ne crée pas de point de rebroussement. | 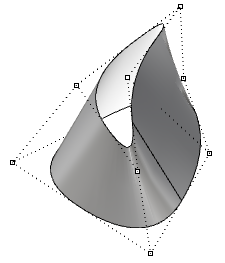 |
Singularité des surfaces NURBS
Prenons par exemple un bord linéaire sur un plan simple, si les deux points de contrôle des extrémités d’un bord sont déplacés pour qu’ils se superposent au milieu, on obtiendra un bord singulier. Vous remarquerez que les courbes isoparamétriques de la surface convergent au point singulier.
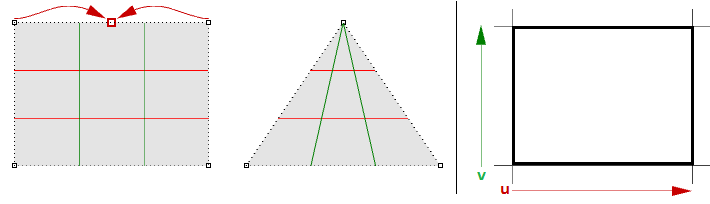
La forme triangulaire ci-dessus peut être créée sans singularité. Vous pouvez limiter une surface avec une polyligne triangulaire. Lorsque vous analysez la structure NURBS sous-jacente, vous constatez que la forme rectangulaire est conservée.
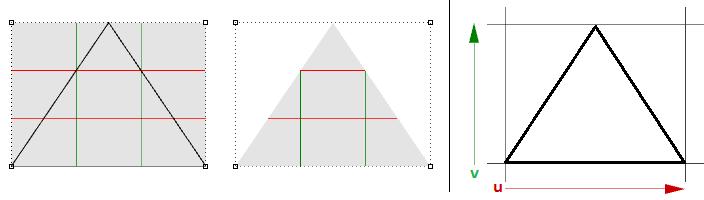
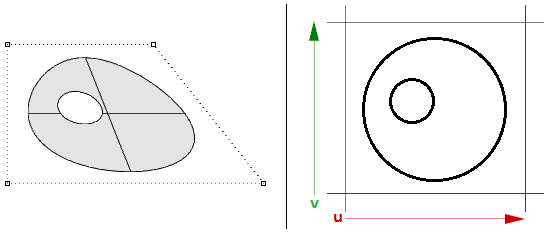
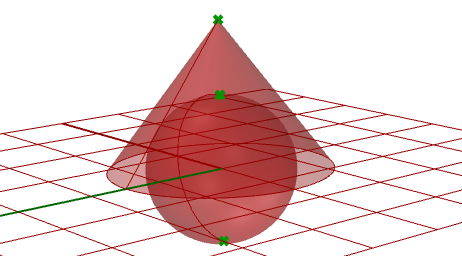
Il est également difficile de générer des cônes et des sphères sans créer de singularité. Le bord correspondant à la pointe d’un cône ainsi que les bords correspondant aux pôles d’une sphère sont réduits en un seul point. Qu’il y ait une singularité ou non, l’espace paramétrique conserve une région plus ou moins rectangulaire.
Surfaces NURBS limitées
Les surfaces NURBS peuvent être limitées ou non limitées. Les surfaces limitées utilisent une surface NURBS sous-jacente et des courbes fermées pour limiter une partie de cette surface. Chaque surface possède une courbe fermée qui définit la bordure extérieure (boucle extérieure) et peut avoir des courbes intérieures fermées ne se croisant pas qui définissent les trous (boucles intérieures). Une surface avec une boucle extérieure identique à celle de sa surface NURBS sous-jacente et ne possédant pas de trou est appelée une surface non limitée.
3.9 Polysurfaces
Une polysurface est composée de plusieurs surfaces NURBS (limitées ou non) jointes ensemble. Chaque surface possède une structure, une paramétrisation, des directions isoparamétriques qui lui sont propres et peuvent ne pas correspondre avec celles des autres. Les polysurfaces sont représentées en utilisant la représentation par les bords (* BRep*). La structure BRep décrit des surfaces, des bords et des sommets avec, entre autres, des données de limite et une connectivité. Les surfaces limitées sont également représentées en utilisant une structure de données BRep.

Une BRep est une structure de données qui décrit chaque face en termes de surface sous-jacente, bords 3D extérieurs, sommets, limites 2D de l’espace paramétrique et relation entre les faces voisines. Les objets BRep sont également appelés des solides lorsqu’ils sont fermés (étanches).
Une boîte simple constituée de six surfaces non limitées jointes est un exemple de polysurface.
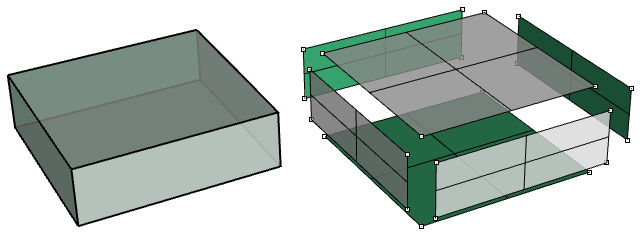
La même boîte peut être créée en utilisant des surfaces limitées, comme celle du dessus dans l’exemple suivant.
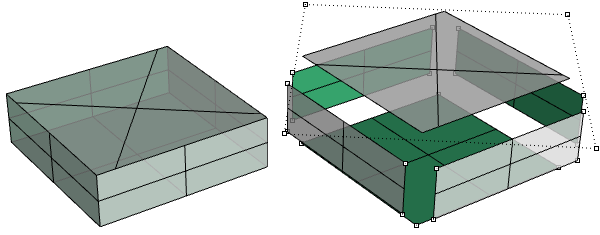
Les faces supérieure et inférieure du cylindre de l’exemple suivant sont limitées à partir de surfaces planes.
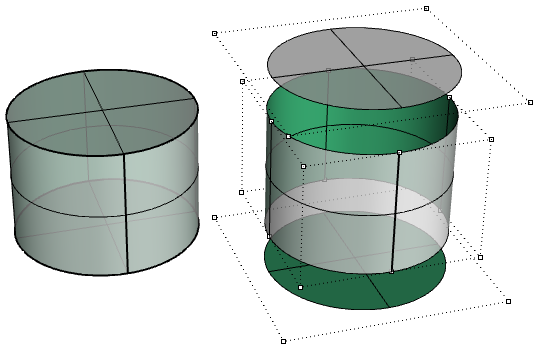
Nous avons vu que l’édition de courbes et surfaces non limitées NURBS est intuitive et peut se faire de manière interactive en déplaçant les points de contrôle. Cependant, l’édition de surfaces et polysurfaces limitées peut s’avérer plus compliquée. La principale difficulté consiste à garder les bords des différentes jointures dans les limites de la tolérance souhaitée. Les faces voisines ayant des bords en commun peuvent être limitées et ne pas avoir la même structure NURBS, la modification de l’objet de sorte que le bord commun soit déformé peut alors entraîner la création d’un espace vide au niveau du bord.
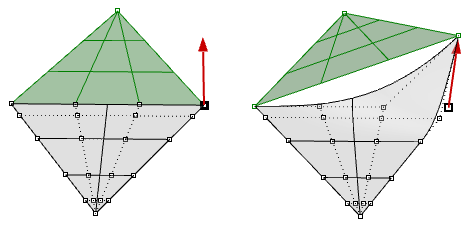
D’autre part, il est souvent beaucoup plus difficile de contrôler le résultat, en particulier lors de l’édition d’une géométrie limitée.
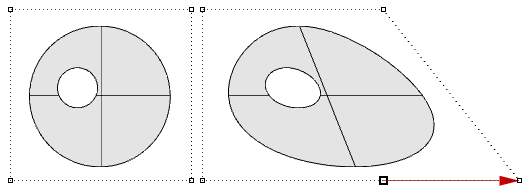
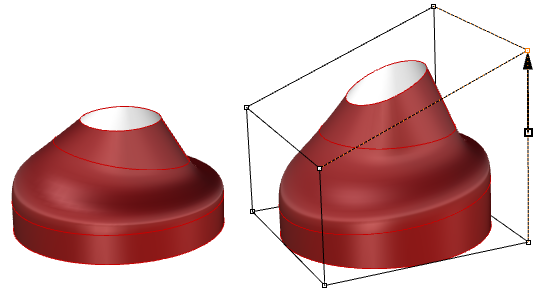
Les surfaces limitées sont décrites dans l’espace de paramétrisation en utilisant la surface sous-jacente non limitée combinée avec les courbes 2D qui se traduisent en bords 3D sur la surface 3D.
3.10 Tutoriels
Les tutoriels suivants utilisent les concepts abordés dans ce chapitre. Ils utilisent Rhinoceros 5 et Grasshopper 0.9.
3.10.1 Continuité entre courbes
Étudier la continuité entre deux courbes de départ. La continuité part du principe que les courbes se rencontrent à la fin de la première courbe et au début de la deuxième.
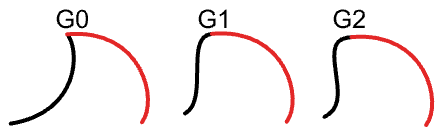
Données de départ :
Deux courbes.
Paramètres :
Calculer les données suivantes afin de déterminer la continuité entre les deux courbes :
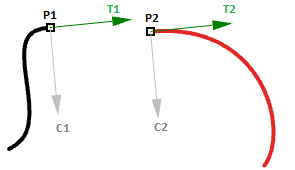
- Le point final de la première courbe ( $$P1$$).
- Le point de départ de la deuxième courbe ( $$P2$$).
- La tangente à la fin de la première courbe et au début de la deuxième ( $$T1$$ et $$T2$$).
- La courbure à la fin de la première courbe et au début de la deuxième ( $$C1$$ et $$C2$$).
Solution :
1. Reparamétrer les courbes de départ. Cette opération permet de savoir que le début de la courbe est calculé à
$$t=0$$ et la fin à
$$t=1$$.
2. Extraire les points de départ et final des deux courbes et vérifier qu’ils coïncident. Si c’est le cas, la continuité entre les deux courbes est au moins
$$G0$$.
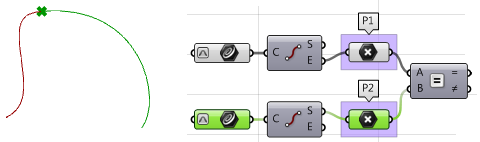
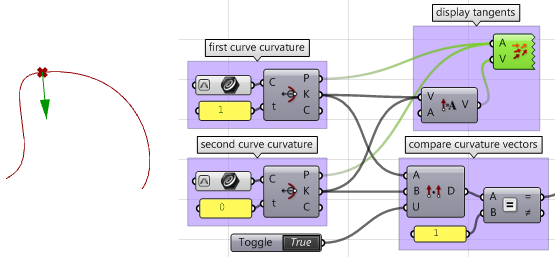
3. Calculer les tangentes.
4. Comparer les tangentes en utilisant le produit scalaire. Attention à bien utiliser les vecteurs unitaires. Si les courbes sont parallèles, la continuité est au moins
$$G1$$.
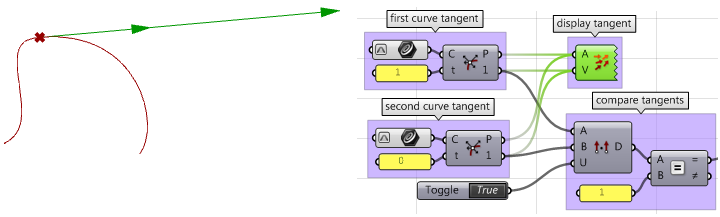
5. Calculer les vecteurs de courbure.
6. Comparer les vecteurs de courbure, et s’ils coïncident, alors les deux courbes présentent une continuité
$$G2$$.
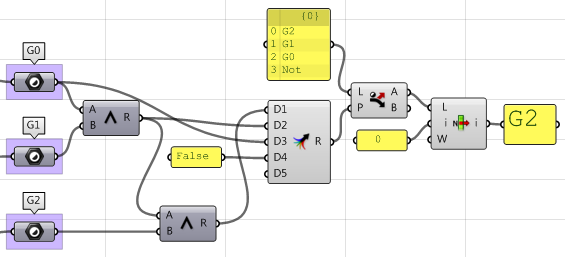
7. Créer une logique permettant de filtrer les trois résultats (G1, G2 et G3) et de sélectionner la continuité la plus élevée.
En utilisant le composant VBScript de Grasshopper :
Private Sub RunScript(ByVal c1 As Curve, ByVal c2 As Curve, ByRef A As Object)
'declare variables
Dim continuity As New String("")
Dim t1, t2 As Double
Dim v_c1, v_c2, c_c1, c_c2 As Vector3d
'extract start and end points
Dim end_c1 = c1.PointAtEnd
Dim start_c2 = c2.PointAtStart
'check G0 continuity
If end_c1.DistanceTo(start_c2) = 0 Then
continuity = "G0"
End If
'check G1 continuity
If continuity = "G0" Then
'calculate tangents
v_c1 = c1.TangentAtEnd
v_c2 = c2.TangentAtStart
'unitize tangent vectors
v_c1.Unitize
v_c2.Unitize
'compare tangents
If v_c1 * v_c2 = 1.0 Then
continuity = "G1"
End If
End If
'check G2 continuity
If continuity = "G1" Then
'extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max
t2 = c2.Domain.Min
'calculate curvature
c_c1 = c1.CurvatureAt(t1)
c_c2 = c2.CurvatureAt(t2)
'unitize curvature vectors
c_c1.Unitize
c_c2.Unitize
'compare vectors
If c_c1 * c_c2 = 1.0 Then
continuity = "G2"
End If
End If
'Assign output
A = continuity
End Sub
En utilisant le composant Python de Grasshopper :
#decclare variables
continuity = ""
#extract start and end points
end_c1 = c1.PointAtEnd
start_c2 = c2.PointAtStart
#check G0 continuity
if end_c1.DistanceTo(start_c2) == 0:
continuity = "G0"
#check G1 continuity
if continuity == "G0":
#calculate tangents
v_c1 = c1.TangentAtEnd
v_c2 = c2.TangentAtStart
#unitize tangent vectors
v_c1.Unitize()
v_c2.Unitize()
#compare tangents
dot = v_c1 * v_c2
if dot == 1.0:
continuity = "G1"
else:
print("Failed G1")
print(dot)
#check G2 continuity
if continuity == "G1":
#extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max
t2 = c2.Domain.Min
#calculate curvature
c_c1 = c1.CurvatureAt(t1)
c_c2 = c2.CurvatureAt(t2)
#unitize curvature vectors
c_c1.Unitize()
c_c2.Unitize()
#compare vectors
dot = c_c1 * c_c2
if dot == 1.0:
continuity = "G2"
else:
print("Failed G2")
print(dot)
#assign output
A = continuity
En utilisant le composant C# de Grasshopper :
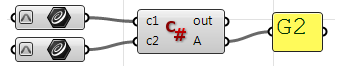
Private Sub RunScript(ByVal c1 As Curve, ByVal c2 As Curve, ByRef A As Object)
//decalre variables
string continuity = ("");
double t1, t2;
Vector3d v_c1, v_c2, c_c1, c_c2;
//extract start and end points
Point3d end_c1 = c1.PointAtEnd;
Point3d start_c2 = c2.PointAtStart;
//check G0 continuity
if( end_c1.DistanceTo(start_c2) == 0){
continuity = "G0";
}
//check G1 continuity
if( continuity == "G0")
{
//calculate tangents
v_c1 = c1.TangentAtEnd;
v_c2 = c2.TangentAtStart;
//unitize tangent vectors
v_c1.Unitize();
v_c2.Unitize();
//compare tangents
if( v_c1 * v_c2 == 1.0 ){
continuity = "G1";
}
}
//check G2 continuity
if( continuity == "G1" )
{
//extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max;
t2 = c2.Domain.Min;
//calculate curvature
c_c1 = c1.CurvatureAt(t1);
c_c2 = c2.CurvatureAt(t2);
//unitize curvature vectors
c_c1.Unitize();
c_c2.Unitize();
//compare vectors
if( c_c1 * c_c2 == 1.0 ){
continuity = "G2";
}
}
//assign output
A = continuity;
End Sub
3.10.2 Surfaces avec une singularité
Extraire les points singuliers d’une sphère et d’un cône.
Données de départ :
Une sphère et un cône.
Paramètres :
La singularité peut être détectée en analysant les limites de l’espace paramétrique 2D possédant des bords non valides ou de longueur nulle. Ces limites devraient être singulières.
Solution :
- Traverser toutes les limites des objets de départ.
- Vérifier si une des limites possède un bord invalide et marquer ce bord en tant que limite singulière.
- Extraire la position des points dans l’espace 3D.
En utilisant le composant VB de Grasshopper :
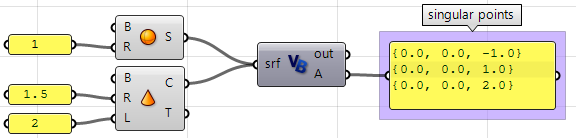
Private Sub RunScript(ByVal srf As Brep, ByRef A As Object)
'Decalre a new list of points
Dim singular_points As New List( Of Point3d)
'Examine all trims in the input
For Each trim As BrepTrim In srf.Trims
'Null edge of a trim indicates a singularity
If trim.Edge Is Nothing Then
'Find the 2D parameter space point of the start or end of the trim
Dim pt2d = New Point2d(trim.PointAtStart)
'Evaluate trim end point on the object surface
Dim pt3d = trim.Face.PointAt(pt2d.x, pt2d.y)
'Add 3D point to the list of singular points
singular_points.Add(pt3d)
End If
Next
'Asign output
A = singular_points
End Sub
En utilisant le composant Python de Grasshopper :
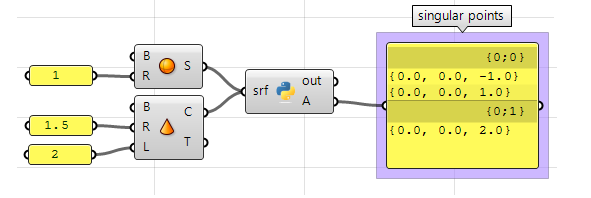
#Decalre a new list of points
singular_points = []
#Examine all trims in the input brep
for trim in srf.Trims:
#Null edge of a trim indicates a singularity
if trim.Edge == None:
#Find the 2D parameter space point at trim start or end
pt2d = trim.PointAtStart
#Evaluate trim end point on the object surface
pt3d = trim.Face.PointAt(pt2d.X, pt2d.Y)
#Add 3D point to the list of singular points
singular_points.append(pt3d)
#Asign output
A = singular_points
En utilisant le composant C# de Grasshopper :
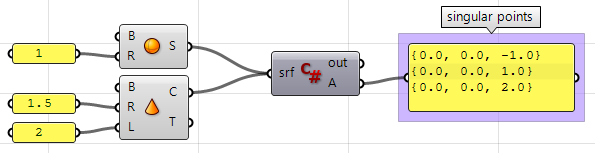
private void RunScript(Brep srf, ref object A)
{
//Decalre a new list of points
List < Point3d > singular_points = new List<Point3d>();
//Examine all trims in the input
foreach( BrepTrim trim in srf.Trims)
{
//Null edge of a trim indicates a singularity
if( trim.Edge == null)
{
//Find the 2D parameter space point of the start or end of the trim
Point2d pt2d = new Point2d(trim.PointAtStart);
//Evaluate trim end point on the object surface
Point3d pt3d = trim.Face.PointAt(pt2d.X, pt2d.Y);
//Add 3D point to the list of singular points
singular_points.Add(pt3d);
}
}
//Asign output
A = singular_points
}
Téléchargement de fichiers d’exemple
Téléchargez le fichier math-samplesandtutorials.zip, qui contient tous les exemples de Grasshopper et les fichiers de code de ce guide.
Étapes suivantes
Pour aller plus loin, consultez le guide Références pour en savoir plus sur la structure détaillée des courbes et des surfaces NURBS.

