Un vecteur indique une quantité, telle que la vitesse ou la force, et possède une direction et une longueur. Les vecteurs sont représentés dans les repères en 3D par un ensemble de trois nombres réels, par exemple :
$$\mathbf{\vec v} = <a_1, a_2, a_3>$$1.1 Représentation vectorielle
Dans ce document, les lettres minuscules en gras avec une flèche au-dessus représentent des vecteurs. Les composants des vecteurs sont indiqués entre chevrons (< >). Les lettres majuscules représentent des points. Les coordonnées seront toujours indiquées entre parenthèses.
À l’aide d’un repère et d’un ensemble de points de référence dans celui-ci, nous pouvons représenter ou visualiser ces vecteurs en utilisant un segment de ligne. Une pointe de flèche indique la direction du vecteur.
Par exemple, un vecteur dont la direction est parallèle à l’axe des x d’un repère et la longueur de 5 unités sera noté ainsi :
$$\mathbf{\vec v} = <5, 0, 0>$$Pour représenter ce vecteur, nous avons besoin d’un point de référence dans le repère. Toutes les flèches de cette figure correspondent par exemple à la représentation d’un même vecteur, même si leur position diffère.
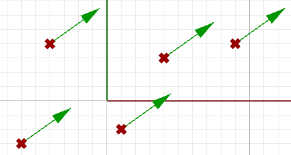
$$A(x,y,z)$$ à un point $$B(x+a_1, y+a_2, z+a_3)$$ sont les représentations équivalentes d’un vecteur $$\vec v$$.
Alors, comment définir les extrémités d’un segment de ligne qui représente un vecteur donné ? Définissons un point de référence (A) de sorte que :
$$A = (1, 2, 3)$$Et un vecteur :
$$\mathbf{\vec v} = <5, 6, 7>$$Le point de l’extrémité de la flèche du vecteur $$(B)$$ est calculé en ajoutant les composants correspondants du point de référence et du vecteur $$\vec v$$ :
$$B = A + \mathbf{\vec v}$$
$$B = (1+5, 2+6, 3+7) $$
$$B = (6, 8, 10)$$
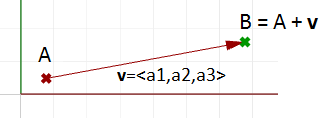
Vecteur de position
Une représentation vectorielle particulière utilise l’ $$\text{origine} (0,0,0)$$ comme point de référence du vecteur. Le vecteur de position $$\mathbf{\vec v} = <a_1,a_2,a_3>$$ est représenté par un segment de ligne entre deux points, l’rigine et le point B, de sorte que :
$$\text{Origine} = (0,0,0)$$
$$B = (a_1,a_2,a_3)$$
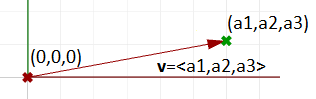
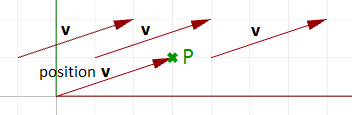
Vecteurs et points
Attention à ne pas confondre vecteurs et points. Ces deux concepts sont différents. Les vecteurs, comme nous venons de le voir, représentent une quantité possédant une direction et une longueur, alors que les points indiquent une position. Par exemple, la direction du nord est un vecteur, alors que le pôle nord est une position (point). Imaginons un vecteur et un point dont les composants sont identiques :
$$\mathbf{\vec v} = <3,1,0>$$
$$P = (3,1,0)$$
Ce vecteur et ce point peuvent être dessinés ainsi :
Longueur d’un vecteur
Comme mentionné auparavant, les vecteurs ont une longueur. Nous utiliserons la notation $$\vert a \vert$$ pour représenter la longueur d’un vecteur $$ a $$ donné. Par exemple :
$$\mathbf{\vec a} = <4, 3, 0>$$
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5$$
En règle générale, la longueur d’un vecteur $$\mathbf{\vec a} <a_1,a_2,a_3>$$ est calculée de la façon suivante :
$$\vert \mathbf{\vec a} \vert = \sqrt{(a_1)^2 + (a_2)^2 + (a_3)^2} $$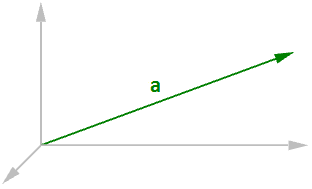
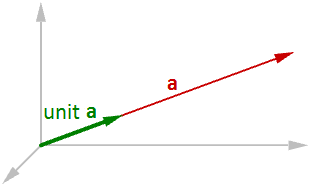
Vecteur unitaire
Un vecteur unitaire est un vecteur dont la longueur est égale à une unité. Les vecteurs unitaires sont couramment utilisés pour comparer les directions de vecteurs.
Pour calculer un vecteur unitaire, nous devons trouver la longueur d’un vecteur donné puis diviser les composants du vecteur par la longueur. Par exemple :
$$\mathbf{\vec a} = <4, 3, 0>$$
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5 \text{ unités de long}$$
Si
$$\mathbf{\vec b} = \text{vecteur unitaire}$$ de
$$a$$, alors :
$$\mathbf{\vec b} = <4/5, 3/5, 0/5>$$
$$\mathbf{\vec b} = <0.8, 0.6, 0>$$
$$\vert \mathbf{\vec b} \vert = \sqrt{0.8^2 + 0.6^2 + 0^2}$$
$$\vert \mathbf{\vec b} \vert = \sqrt{0.64 + 0.36 + 0}$$
$$\vert \mathbf{\vec b} \vert = \sqrt{(1)} = 1 \text{ unité de long}$$
Par définition :
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$Le vecteur unitaire de $$\mathbf{\vec a} = <a_1/\vert \mathbf{\vec a} \vert , a_2/\vert \mathbf{\vec a} \vert , a_3/\vert \mathbf{\vec a} \vert >$$
1.2 Opérations sur les vecteurs
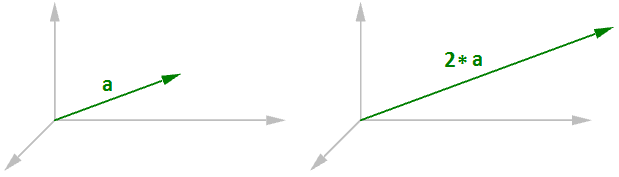
Produit d’un vecteur par un scalaire
Le produit d’un vecteur par un scalaire revient à multiplier un vecteur par un nombre. Par exemple :
$$\mathbf{\vec a} = <4, 3, 0>$$
$$2* \mathbf{\vec a} = <24, 23, 2*0>$$
$$2*\mathbf{\vec a} = <8, 6, 0>$$
Soient un vecteur $$\mathbf{\vec a} = <a_1, a_2, a_3>$$ et un nombre réel $$t$$
$$t*\mathbf{\vec a} = < t* a_1, t* a_2, t* a_3 >$$Somme de deux vecteurs
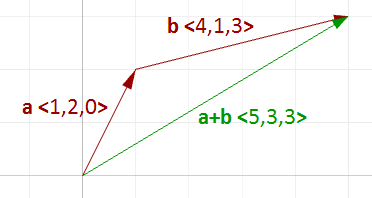
La somme de deux vecteurs produit un troisième vecteur à partir de deux vecteurs de départ. Pour ajouter deux vecteurs, il faut ajouter leurs composants.
Par exemple, soient deux vecteurs :
$$\mathbf{\vec a} = <1, 2, 0> $$
$$\mathbf{\vec b} = <4, 1, 3> $$
$$\mathbf{\vec a}+\mathbf{\vec b} = <1+4, 2+1, 0+3>$$
$$\mathbf{\vec a}+\mathbf{\vec b} = <5, 3, 3>$$
En général, la somme de deux vecteurs a et b est calculée de cette façon :
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a}+\mathbf{\vec b} = <a_1+b_1, a_2+b_2, a_3+b_3>$$
La somme de plusieurs vecteurs est utile pour trouver la direction moyenne de ces vecteurs. On utilise normalement pour cela des vecteurs de même longueur. Voici un exemple montrant la différence entre la somme de vecteurs de même longueur et la somme de vecteurs de différentes longueurs :
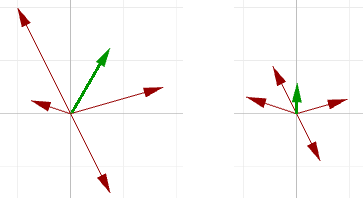
Les vecteurs de départ ne seront probablement pas de même longueur. Afin de trouver la direction moyenne, vous devez utiliser le vecteur unitaire des vecteurs de départ. Comme indiqué précédemment, le vecteur unitaire est un vecteur dont la longueur est égale à 1.
Soustraction de vecteurs
La soustraction de deux vecteurs produit un troisième vecteur à partir de deux vecteurs de départ. Pour soustraire deux vecteurs, il faut soustraire les composants correspondants. Par exemple, soient deux vecteurs $$\mathbf{\vec a}$$ et $$\mathbf{\vec b}$$, si on soustrait $$\mathbf{\vec b}$$ de $$\mathbf{\vec a}$$ alors :
$$\mathbf{\vec a} = <1, 2, 0> $$
$$\mathbf{\vec b} = <4, 1, 4> $$
$$\mathbf{\vec a}-\mathbf{\vec b} = <1-4, 2-1, 0-4>$$
$$\mathbf{\vec a}-\mathbf{\vec b} = <-3, 1, -4> = \mathbf{\mathbf{\vec b}a}$$
Si on soustrait $$\mathbf{\vec a}$$ de $$\mathbf{\vec b}$$, le résultat est différent :
$$\mathbf{\vec b} - \mathbf{\vec a} = <4-1, 1-2, 4-0>$$
$$\mathbf{\vec b} - \mathbf{\vec a} = <3, -1, 4> = \mathbf{\mathbf{\vec a}b}$$
Vous remarquerez que le vecteur $$\mathbf{\vec b} - \mathbf{\vec a}$$ est de même longueur que le vecteur $$\mathbf{\vec a} - \mathbf{\vec b}$$ mais leur direction est opposée.
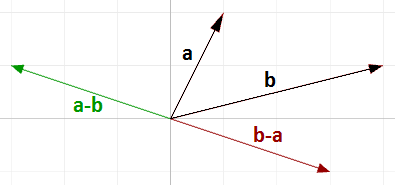
Soient deux vecteurs, $$\mathbf{\vec a}$$ et $$\mathbf{\vec b}$$, alors par définition $$\mathbf{\vec a} - \mathbf{\vec b}$$ est un vecteur calculé de cette façon :
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a}-\mathbf{\vec b} = <a_1 - b_1, a_2 - b_2, a_3 - b_3> = \mathbf{\mathbf{\vec b}a}$$
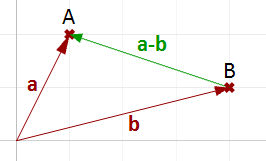
La soustraction de vecteurs est couramment utilisée pour trouver des vecteurs entre des points. Ainsi, pour trouver le vecteur allant de l’extrémité de la flèche du vecteur de position $$\mathbf{\vec b}$$ jusqu’à l’extrémité de la flèche du vecteur de position $$\mathbf{\vec a}$$, on utilise la soustraction de vecteurs $$(\mathbf{\vec a}-\mathbf{\vec b})$$ comme indiqué sur la Figure (11).
Propriétés des vecteurs
Les vecteurs possèdent 8 propriétés. Si a, b et c sont des vecteurs, et s et t des nombres, alors :
$$\mathbf{\vec a} + \mathbf{\vec b} = \mathbf{\vec b} + \mathbf{\vec a}$$
$$\mathbf{\vec a} + 0 = a$$
$$s * (\mathbf{\vec a} + \mathbf{\vec b}) = s * a + s * \mathbf{\vec b}$$
$$s * t * (\mathbf{\vec a}) = s * (t * \mathbf{\vec a})$$
$$\mathbf{\vec a} + (\mathbf{\vec b} + \mathbf{\vec c}) = (\mathbf{\vec a} + \mathbf{\vec b}) + \mathbf{\vec c}$$
$$\mathbf{\vec a} + (-\mathbf{\vec a}) = 0$$
$$(s + t) * \mathbf{\vec a} = s * \mathbf{\vec a} + t * \mathbf{\vec a}$$
$$1 * \mathbf{\vec a} = \mathbf{\vec a}$$
Produit scalaire de vecteurs
Le produit scalaire de deux vecteurs génère un nombre à partir de deux vecteurs. Par exemple, soient deux vecteurs a et b :
$$\mathbf{\vec a} = <1, 2, 3> $$
$$\mathbf{\vec b} = <5, 6, 7>$$
Le produit scalaire de ces deux vecteurs est la somme de la multiplication des composants :
$$\mathbf{\vec a} · \mathbf{\vec b} = 1 * 5 + 2 * 6 + 3 * 7$$
$$\mathbf{\vec a} · \mathbf{\vec b} = 38$$
Soient deux vecteurs a et b, par définition :
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a} · \mathbf{\vec b} = a_1 * b_1 + a_2 * b_2 + a_3 * b_3$$
Le résultat d’un produit scalaire entre deux vecteurs est toujours un nombre positif si les deux vecteurs ont la même direction générale. Si la direction générale des deux vecteurs est opposée, alors le résultat du produit scalaire est négatif.
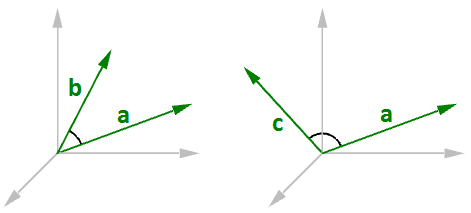
Le résultat du produit scalaire de deux vecteurs unitaires est toujours entre -1 et +1. Par exemple :
$$\mathbf{\vec a} = <1, 0, 0>$$
$$\mathbf{\vec b} = <0,6, 0,8, 0>$$
$$\mathbf{\vec a} · \mathbf{\vec b} = (1 * 0.6, 0 * 0.8, 0 * 0) = 0.6$$
De plus, le produit scalaire d’un vecteur par lui-même est égal à la longueur du vecteur puissance deux. Par exemple :
$$\mathbf{\vec a} = <0, 3, 4>$$
$$\mathbf{\vec a} · \mathbf{\vec a} = 0 * 0 + 3 * 3 + 4 * 4 $$
$$\mathbf{\vec a} · \mathbf{\vec a} = 25$$
Calcul de la longueur au carré du vecteur $$\mathbf{\vec a}$$ :
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5$$
$$\vert \mathbf{\vec a} \vert 2 = 25$$
Produit scalaire de vecteurs, longueurs et angles
Il existe une relation entre le produit scalaire de deux vecteurs et l’angle entre les deux vecteurs.
Par définition :
$$\mathbf{\vec a} · \mathbf{\vec b} = \vert \mathbf{\vec a} \vert * \vert \mathbf{\vec b} \vert * cos(ө)$$ , or
$$\mathbf{\vec a} · \mathbf{\vec b} / (\vert \mathbf{\vec a} \vert * \vert \mathbf{\vec b} \vert) = cos(ө)$$
Où :
$$ө$$ est l’angle inclus entre les vecteurs.
Si les vecteurs a et b sont des vecteurs unitaires, on peut dire que :
$$\mathbf{\vec a} · \mathbf{\vec b} = cos(ө)$$Et puisque le cosinus d’un angle de 90 degrés est égal à 0, on peut dire que :
Par exemple, si on calcule le produit scalaire de deux vecteurs orthogonaux, l’axe des x et l’axe des y du repère général, le résultat sera égal à zéro.
$$\mathbf{\vec x} = <1, 0, 0>$$
$$\mathbf{\vec y} = <0, 1, 0>$$
$$\mathbf{\vec x} · \mathbf{\vec y} = (1 * 0) + (0 * 1) + (0 * 0)$$
$$\mathbf{\vec x} · \mathbf{\vec y} = 0$$
Il existe également une relation entre le produit scalaire et la longueur de projection d’un vecteur sur un autre. Par exemple :
$$\mathbf{\vec a} = <5, 2, 0>$$
$$\mathbf{\vec b} = <9, 0, 0>$$
$$(\mathbf{\vec b})unitaire = <1, 0, 0>$$
$$\mathbf{\vec a} · (\mathbf{\vec b})unitaire = (5 * 1) + (2 * 0) + (0 * 0) $$
$$\mathbf{\vec a} · (\mathbf{\vec b})unitaire = 2 (\text{qui est égal à la longueur de projection du vecteur a sur le vecteur b})$$

Soient un vecteur a et un vecteur non nul b, par définition on peut calculer la longueur de projection pL du vecteur a sur le vecteur b en utilisant le produit scalaire.
$$pL = \vert \mathbf{\vec a} \vert * cos(ө) $$
$$pL = \mathbf{\vec a} · (\mathbf{\vec b})unitaire$$
Propriétés du produit scalaire
Soient les vecteurs $$\mathbf{\vec a}$$, $$\mathbf{\vec b}$$ et $$\mathbf{\vec c}$$ et le nombre s, alors :
$$\mathbf{\vec a} · \mathbf{\vec a} = \vert \mathbf{\vec a} \vert ^2$$
$$\mathbf{\vec a} · (\mathbf{\vec b} + \mathbf{\vec c}) = \mathbf{\vec a} · \mathbf{\vec b} + \mathbf{\vec a} · \mathbf{\vec c}$$
$$0 · \mathbf{\vec a} = 0$$
$$\mathbf{\vec a} · \mathbf{\vec b} = \mathbf{\vec b} · \mathbf{\vec a}$$
$$(s * \mathbf{\vec a}) · \mathbf{\vec b} = s * (\mathbf{\vec a} · \mathbf{\vec b}) = \mathbf{\vec a} · (s * \mathbf{\vec b})$$
Produit vectoriel
Le produit vectoriel de deux vecteurs produit un troisième vecteur orthogonal aux deux vecteurs de départ.
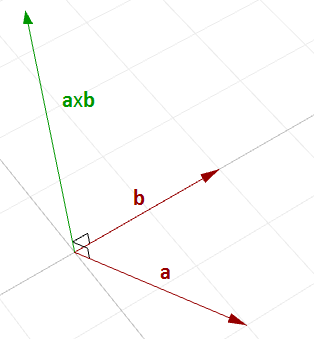
Par exemple, si vous avez deux vecteurs reposant sur le plan xy du repère général, leur produit vectoriel est un vecteur perpendiculaire au plan xy dans la direction positive ou négative de l’axe des z du repère général. Par exemple :
$$\mathbf{\vec a} = <3, 1, 0>$$
$$\mathbf{\vec b} = <1, 2, 0>$$
$$\mathbf{\vec a} × \mathbf{\vec b} = < (1 * 0 – 0 * 2), (0 * 1 - 3 * 0), (3 * 2 - 1 * 1) > $$
$$\mathbf{\vec a} × \mathbf{\vec b} = <0, 0, 5>$$
Vous n’aurez probablement jamais à calculer un produit vectoriel de deux vecteurs à la main, mais si vous voulez savoir comment faire, continuez la lecture ; sinon vous pouvez ignorer cette section. Le produit vectoriel $$a × b$$ est défini en utilisant des déterminants. Voici une illustration simple du calcul d’un déterminant en utilisant des vecteurs de base standards :
$$ \color {red}{i} = <1, 0, 0>$$
$$ \color {blue}{j} = <0,1, 0>$$
$$ \color {green}{k} = <0, 0, 1>$$
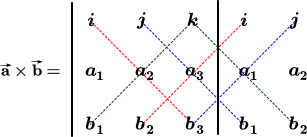
Le produit vectoriel des deux vecteurs $$\mathbf{\vec a} = <a1, a2, a3>$$ et $$\mathbf{\vec b} = <b1, b2, b3>$$ est calculé ainsi en utilisant le tableau ci-dessus :
$$\mathbf{\vec a} × \mathbf{\vec b} = \color {red}{i (a_2 * b_3)} + \color {blue}{ j (a_3 * b_1)} + \color {green}{k(a_1 * b_2)} - \color {green}{k (a_2 * b_1)} - \color {red}{i (a_3 * b_2)} -\color {blue}{ j (a_1 * b_3)}$$
$$\mathbf{\vec a} × \mathbf{\vec b} = \color {red}{i (a_2 * b_3 - a_3 * b_2)} + \color {blue}{j (a_3 * b_1 - a_1 * b_3)} +\color {green}{k (a_1 * b_2 - a_2 * b_1)}$$
$$\mathbf{\vec a} × \mathbf{\vec b} = <\color {red}{a_2 * b_3 – a_3 * b_2}, \color {blue}{a_3 * b_1 - a_1 * b_3}, \color {green}{a_1 * b_2 - a_2 * b_1} >$$
Produit vectoriel et angle entre les vecteurs
Il existe une relation entre l’angle formé par deux vecteurs et la longueur du vecteur résultat du produit vectoriel. Plus l’angle est petit (sinus plus petit), plus le vecteur du produit vectoriel est court. L’ordre des opérandes est important dans un produit vectoriel. Par exemple :
$$\mathbf{\vec a} = <1, 0, 0>$$
$$\mathbf{\vec b} = <0, 1, 0>$$
$$\mathbf{\vec a} × \mathbf{\vec b} = <0, 0, 1>$$
$$\mathbf{\vec b} × \mathbf{\vec a} = <0, 0, -1>$$
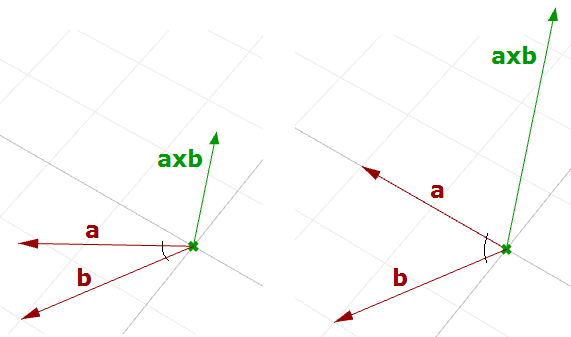
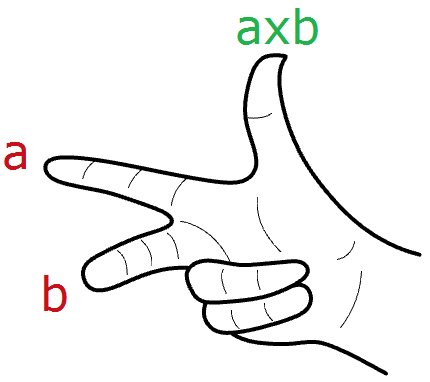
Dans le système de Rhino, la direction de $$\mathbf{\vec a} × \mathbf{\vec b}$$ est donnée par la règle de la main droite (où $$\mathbf{\vec a}$$ = index, $$\mathbf{\vec b}$$ = majeur et $$\mathbf{\vec a} × \mathbf{\vec b}$$ = pouce).
Soit une paire de vecteurs 3D $$\mathbf{\vec a}$$ et $$\mathbf{\vec b}$$, par définition :
$$\vert \mathbf{\vec a} × \mathbf{\vec b} \vert = \vert \mathbf{\vec a} \vert \vert \mathbf{\vec b} \vert sin(ө)$$Où :
$$ө$$ est l’angle inclus entre les vecteurs de position de $$\mathbf{\vec a}$$ et $$\mathbf{\vec b}$$
Si a et b sont des vecteurs unitaires, on peut alors simplement dire que la longueur de leur produit vectoriel est égale au sinus de l’angle qu’ils forment. En d’autres termes :
$$\vert \mathbf{\vec a} × \mathbf{\vec b} \vert = sin(ө)$$Le produit vectoriel entre deux vecteurs nous aide à déterminer si deux vecteurs sont parallèles. En effet, le résultat est toujours égal à un vecteur nul.
Propriétés du produit vectoriel
Soient les vecteurs
$$\mathbf{\vec a}$$,
$$\mathbf{\vec b}$$ et
$$\mathbf{\vec c}$$ et le nombre
$$s$$, alors :
$$\mathbf{\vec a} × \mathbf{\vec b} = -\mathbf{\vec b} × \mathbf{\vec a}$$
$$(s * \mathbf{\vec a}) × \mathbf{\vec b} = s * (\mathbf{\vec a} × \mathbf{\vec b}) = \mathbf{\vec a} × (s * \mathbf{\vec b})$$
$$\mathbf{\vec a} × (\mathbf{\vec b} + \mathbf{\vec c}) = \mathbf{\vec a} × \mathbf{\vec b} + \mathbf{\vec a} × \mathbf{\vec c}$$
$$(\mathbf{\vec a} + \mathbf{\vec b}) × \mathbf{\vec c} = \mathbf{\vec a} × \mathbf{\vec c} + \mathbf{\vec b} × \mathbf{\vec c}$$
$$\mathbf{\vec a} · (\mathbf{\vec b} × \mathbf{\vec c}) = (\mathbf{\vec a} × \mathbf{\vec b}) · \mathbf{\vec c}$$
$$\mathbf{\vec a} × (\mathbf{\vec b} × \mathbf{\vec c}) = (\mathbf{\vec a} · \mathbf{\vec c}) * \mathbf{\vec b} – (\mathbf{\vec a} · \mathbf{\vec b}) * \mathbf{\vec c}$$
1.3 Équation vectorielle d’une ligne
L’équation vectorielle d’une ligne est utilisée dans les applications de modélisation 3D et en infographie.
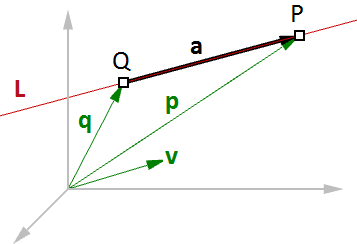
Si on connaît la direction d’une ligne et un point sur cette ligne, on peut alors trouver tous les autres points sur la ligne en utilisant des vecteurs :
$$\overline{L} = ligne$$
$$\mathbf{\vec v} = <a, b, c>$$ - vecteur unitaire définissant la direction de la ligne
$$Q = (x_0, y_0, z_0)$$ point sur la ligne
$$P = (x, y, z)$$ n’importe quel point sur la ligne
On sait que :
$$\mathbf{\vec a} = t *\mathbf{\vec v}$$ (2)
$$\mathbf{\vec p} = \mathbf{\vec q} + \mathbf{\vec a}$$ (1)
À partir de 1 et 2 :
$$\mathbf{\vec p} = \mathbf{\vec q} + t * \mathbf{\vec v}$$ (3)
Cependant, on peut écrire (3) ainsi :
$$<x, y, z> = <x_0, y_0, z_0> + <t * a, t * b, t * c>$$
$$<x, y, z> = <x_0 + t * a, y_0 + t * b, z_0 + t * c>$$
Donc :
$$x = x_0 + t * a$$
$$y = y_0 + t * b$$
$$z = z_0 + t * c$$
Qui équivaut à :
$$P = Q + t * \mathbf{\vec v}$$Autre exemple courant, trouver le milieu entre deux points. La démonstration suivante montre comment trouver le milieu en utilisant l’équation vectorielle d’une ligne :
$$\mathbf{\vec q}$$ est le vecteur de position du point
$$Q$$
$$\mathbf{\vec p}$$ est le vecteur de position du point
$$P$$
$$\mathbf{\vec a}$$ est le vecteur allant de
$$Q \rightarrow P$$
À partir de la soustraction de vecteurs, on sait que :
$$\mathbf{\vec a} = \mathbf{\vec p} - \mathbf{\vec q}$$À partir de l’équation de la ligne, on sait que :
$$M = Q + t * \mathbf{\vec a}$$Et puisqu’on cherche le milieu, alors :
$$t = 0.5$$On peut alors dire que :
$$M = Q + 0.5 * \mathbf{\vec a}$$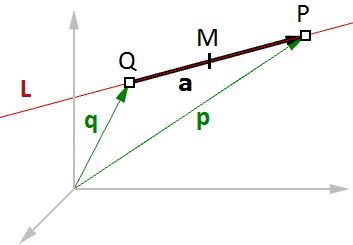
Il est possible de trouver n’importe quel point entre $$Q$$ et $$P$$ en changeant la valeur $$t$$ entre 0 et 1 et en utilisant l’équation générale :
$$M = Q + t * (P - Q)$$1.4 Équation vectorielle d’un plan
Un plan peut être défini par un point et un vecteur perpendiculaire au plan. Ce vecteur est normalement appelé la normale du plan. La normale pointe dans la direction supérieure du plan.
On peut calculer la normale d’un plan lorsqu’on connaît trois points non linéaires sur le plan.
Sur la Figure (18), soient :
$$A$$ = le premier point sur le plan
$$B$$ = le deuxième point sur le plan
$$C$$ = le troisième point sur le plan
Et :
$$\mathbf{\vec a} $$ = un vecteur de position du point
$$A$$
$$\mathbf{\vec b}$$ = un vecteur de position du point
$$B$$
$$\mathbf{\vec c}$$ = un vecteur de position du point
$$C$$
On peut trouver le vecteur de la normale $$\mathbf{\vec n}$$ ainsi :
$$\mathbf{\vec n} = (\mathbf{\vec b} - \mathbf{\vec a}) × (\mathbf{\vec c} - \mathbf{\vec a})$$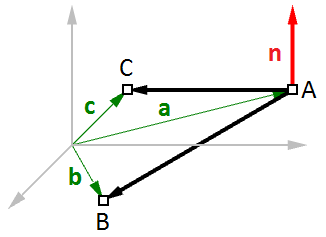
Il est également possible de dériver l’équation scalaire du plan en utilisant le produit scalaire des vecteurs :
$$\mathbf{\vec n} · (\mathbf{\vec b} - \mathbf{\vec a}) = 0$$Si :
$$\mathbf{\vec n} = <a, b, c>$$
$$\mathbf{\vec b} = <x, y, z>$$
$$ \mathbf{\vec a} = <x_0, y_0, z_0>$$
On peut alors développer ce qui précède :
$$<a, b, c> · <x-x_0, y-y_0, z-z_0 > = 0$$La résolution du produit scalaire donne l’équation scalaire générale d’un plan :
$$a * (x - x_0) + b * (y - y_0) + c * (z - z_0) = 0$$1.5 Tutoriels
Tous les concepts que nous avons vus dans ce chapitre sont directement applicables pour résoudre des problèmes de géométrie couramment rencontrés en modélisation. Vous trouverez ci-dessous des tutoriels pas à pas utilisant les concepts abordés dans ce chapitre dans Rhino et Grasshopper (GH).
1.5.1 Direction d’une face
Soient un point et une surface, comment déterminer si le point est devant ou derrière la surface ?
Données de départ :
- une surface
- un point
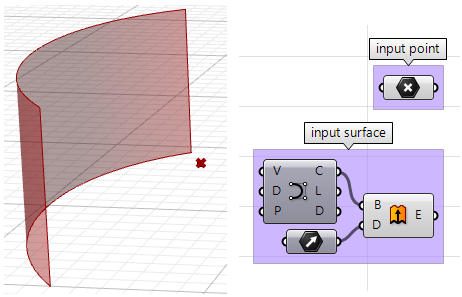
Paramètres :
La direction de la face est définie par la direction normale de la surface. Nous aurons besoin des informations suivantes :
- La direction normale de la surface au point le plus proche du point de départ.
- La direction d’un vecteur à partir du point le plus proche du point de départ.
Comparer les deux directions précédentes, si elles sont les mêmes, le point se trouve devant, sinon il se trouve derrière.
Solution :
1. Trouver la position du point le plus proche sur la surface par rapport au point de départ en utilisant le composant Pull (Attirer). Ceci donnera la position uv du point le plus proche, qui peut ensuite être utilisée pour analyser la surface et trouver sa direction normale.
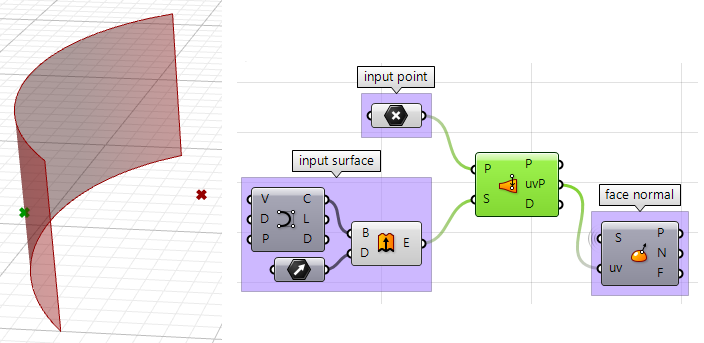
2. On peut maintenant utiliser le point le plus proche pour dessiner un vecteur dirigé vers le point de départ. On peut également dessiner :
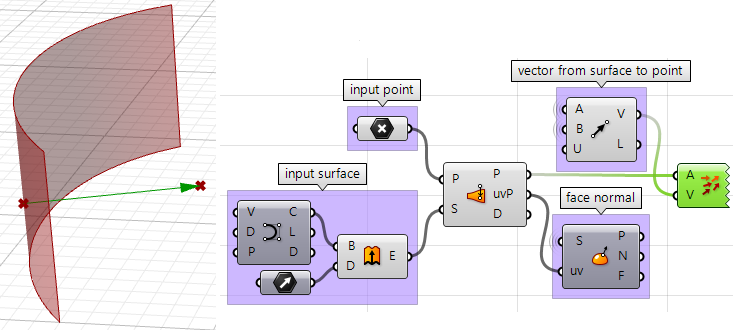
3. Les deux vecteurs peuvent être comparés en utilisant le produit scalaire. Si le résultat est positif, le point se trouve devant la surface. Si le résultat est négatif, le point se trouve derrière la surface.
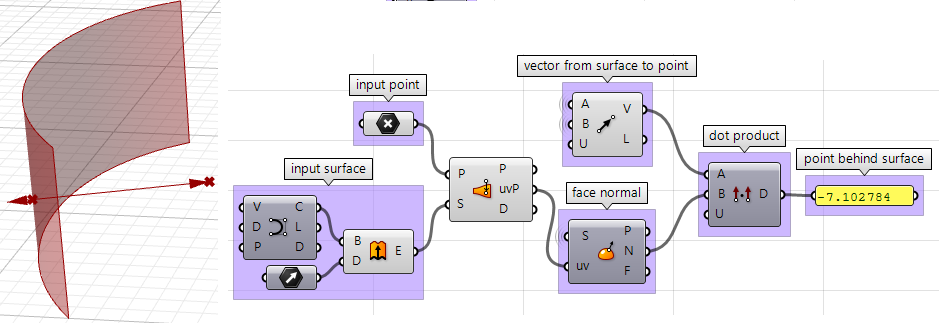
Les étapes précédentes peuvent également être réalisées en utilisant un autre langage d’écriture de scripts. En utilisant le composant VB de Grasshopper :
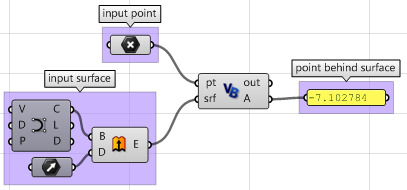
Private Sub RunScript(ByVal pt As Point3d, ByVal srf As Surface, ByRef A As Object)
'Declare variables
Dim u, v As Double
Dim closest_pt As Point3d
'get closest point u, v
srf.ClosestPoint(pt, u, v)
'get closest point
closest_pt = srf.PointAt(u, v)
'calculate direction from closest point to test point
Dim dir As New Vector3d(pt - closest_pt)
'calculate surface normal
Dim normal = srf.NormalAt(u, v)
'compare the two directions using the dot product
A = dir * normal
End Sub
En utilisant le composant Python de Grasshopper avec RhinoScriptSyntax :
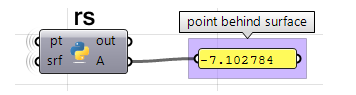
import rhinoscriptsyntax as rs #import RhinoScript library
#find the closest point
u, v = rs.SurfaceClosestPoint(srf, pt)
#get closest point
closest_pt = rs.EvaluateSurface(srf, u, v)
#calculate direction from closest point to test point
dir = rs.PointCoordinates(pt) - closest_pt
#calculate surface normal
normal = rs.SurfaceNormal(srf, [u, v])
#compare the two directions using the dot product
A = dir * normal
En utilisant le composant Python de Grasshopper avec RhinoCommon uniquement :
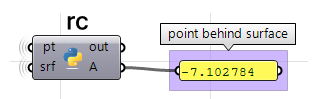
#find the closest point
found, u, v = srf.ClosestPoint(pt)
if found:
#get closest point
closest_pt = srf.PointAt(u, v)
#calculate direction from closest point to test point
dir = pt - closest_pt
#calculate surface normal
normal = srf.NormalAt(u, v)
#compare the two directions using the dot product
A = dir * normal
En utilisant le composant C# de Grasshopper :

private void RunScript(Point3d pt, Surface srf, ref object A)
{
//Declare variables
double u, v;
Point3d closest_pt;
//get closest point u, v
srf.ClosestPoint(pt, out u, out v);
//get closest point
closest_pt = srf.PointAt(u, v);
//calculate direction from closest point to test point
Vector3d dir = pt - closest_pt;
//calculate surface normal
Vector3d normal = srf.NormalAt(u, v);
//compare the two directions using the dot product
A = dir * normal;
}
1.5.2 Décomposition d’une boîte
Le tutoriel suivant montre comment décomposer une polysurface. Voici à quoi ressemble la boîte finale décomposée :
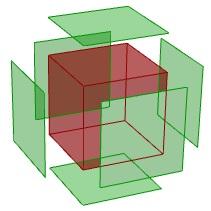
Données de départ :
Identifiez l’objet de départ, qui est une boîte. Nous utiliserons le paramètre Box de GH :

Paramètres :
- Pensez à tous les paramètres dont nous avons besoin afin de réaliser ce tutoriel.
- Le centre de la décomposition.
- Les faces de la boîte que nous décomposons.
- La direction dans laquelle chaque face est déplacée.
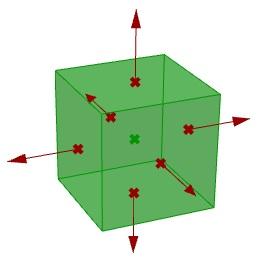
Une fois les paramètres identifiés, il faut les assembler en articulant les étapes logiques afin d’obtenir la solution voulue.
Solution :
1. Trouver le centre de la boîte en utilisant le composant Box Properties de GH :
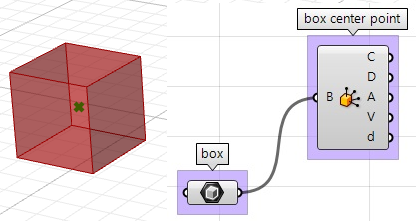
2. Extraire les faces de la boîte avec le composant Deconstruct Brep :
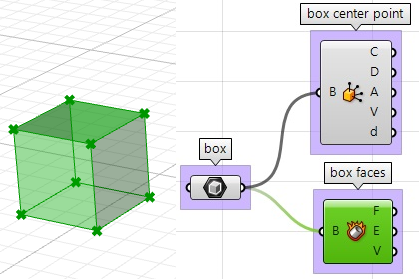
3. La direction dans laquelle les faces sont déplacées est la partie difficile. Il faut tout d’abord trouver le centre de chaque face puis définir la direction à partir du centre de la boîte vers le centre de chaque face comme suit :
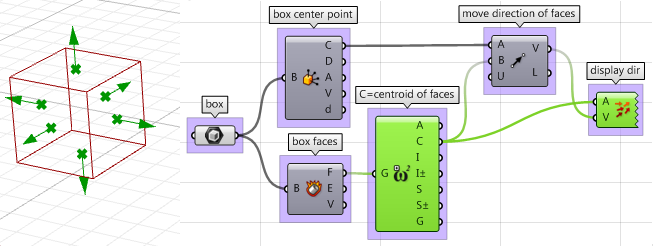
4. Une fois tous les paramètres scriptés, on peut utiliser le composant Move pour déplacer les faces dans la bonne direction. Vérifiez juste que l’amplitude des vecteurs est définie correctement et vous pouvez lancer le processus.
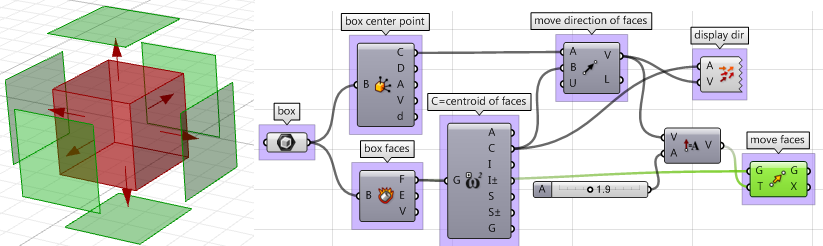
Les étapes précédentes peuvent également être réalisées en utilisant VB script, C# ou Python. Vous trouverez ci-après la solution avec ces langages de scripts.
En utilisant le composant VB de Grasshopper :
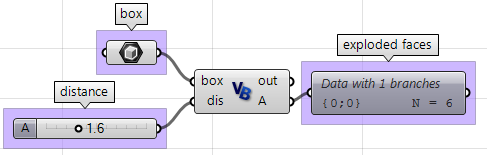
Private Sub RunScript(ByVal box As Brep, ByVal dis As Double, ByRef A As Object)
'get the brep center
Dim area As Rhino.Geometry.AreaMassProperties
area = Rhino.Geometry.AreaMassProperties.Compute(box)
Dim box_center As Point3d
box_center = area.Centroid
'get a list of faces
Dim faces As Rhino.Geometry.Collections.BrepFaceList = box.Faces
'decalre variables
Dim center As Point3d
Dim dir As Vector3d
Dim exploded_faces As New List( Of Rhino.Geometry.Brep )
Dim i As Int32
'loop through all faces
For i = 0 To faces.Count() - 1
'extract each of the face
Dim extracted_face As Rhino.Geometry.Brep = box.Faces.ExtractFace(i)
'get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face)
center = area.Centroid
'calculate move direction (from box centroid to face center)
dir = center - box_center
dir.Unitize()
dir *= dis
'move the extracted face
extracted_face.Transform(Transform.Translation(dir))
'add to exploded_faces list
exploded_faces.Add(extracted_face)
Next
'assign exploded list of faces to output
A = exploded_faces
End Sub
En utilisant le composant Python de Grasshopper avec RhinoCommon :
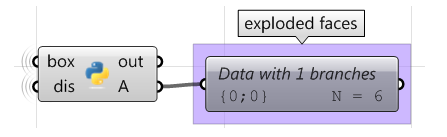
import Rhino
#get the brep center
area = Rhino.Geometry.AreaMassProperties.Compute(box)
box_center = area.Centroid
#get a list of faces
faces = box.Faces
#decalre variables
exploded_faces = []
#loop through all faces
for i, face in enumerate(faces):
#get a duplicate of the face
extracted_face = faces.ExtractFace(i)
#get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face)
center = area.Centroid
#calculate move direction (from box centroid to face center)
dir = center - box_center
dir.Unitize()
dir *= dis
#move the extracted face
move = Rhino.Geometry.Transform.Translation(dir)
extracted_face.Transform(move)
#add to exploded_faces list
exploded_faces.append(extracted_face)
#assign exploded list of faces to output
A = exploded_faces
En utilisant le composant C# de Grasshopper :
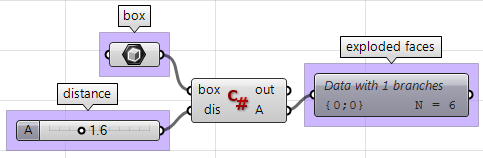
private void RunScript(Brep box, double dis, ref object A)
{
//get the brep center
Rhino.Geometry.AreaMassProperties area = Rhino.Geometry.AreaMassProperties.Compute(box);
Point3d box_center = area.Centroid;
//get a list of faces
Rhino.Geometry.Collections.BrepFaceList faces = box.Faces;
//decalre variables
Point3d center; Vector3d dir;
List<Rhino.Geometry.Brep> exploded_faces = new List<Rhino.Geometry.Brep>();
//loop through all faces for( int i = 0; i < faces.Count(); i++ )
{
//extract each of the face
Rhino.Geometry.Brep extracted_face = box.Faces.ExtractFace(i);
//get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face);
center = area.Centroid;
//calculate move direction (from box centroid to face center)
dir = center - box_center;
dir.Unitize();
dir *= dis;
//move the extracted face
extracted_face.Transform(Transform.Translation(dir));
//add to exploded_faces list
exploded_faces.Add(extracted_face);
}
//assign exploded list of faces to output
A = exploded_faces;
}
1.5.3 Sphères tangentes
Ce tutoriel montrera comment créer deux sphères tangentes entre deux points de départ. Voici à quoi ressemble le résultat :
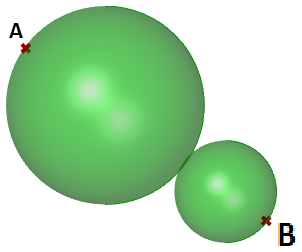
Données de départ :
Deux points (
$$A$$ et
$$B$$) dans le repère 3D.
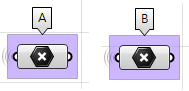
Paramètres : Voici la liste des paramètres dont nous avons besoin pour résoudre ce problème : $$Un$$ point $$D$$ tangent aux deux sphères, au niveau d’un paramètre $$t$$ (0-1) entre les points $$A$$ et $$B$$.
- Le centre de la première sphère ou le milieu $$C1$$ entre $$A$$ et $$D$$.
- Le centre de la deuxième sphère ou le milieu $$C2$$ entre $$D$$ et $$B$$.
- Le rayon de la première sphère $$(r1)$$ ou la distance entre $$A$$ et $$C1$$.
- Le rayon de la deuxième sphère $$(r2)$$ ou la distance entre $$D$$ et $$C2$$.
Solution :
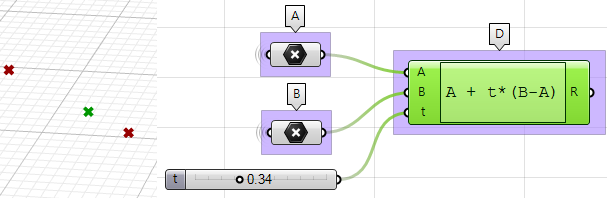
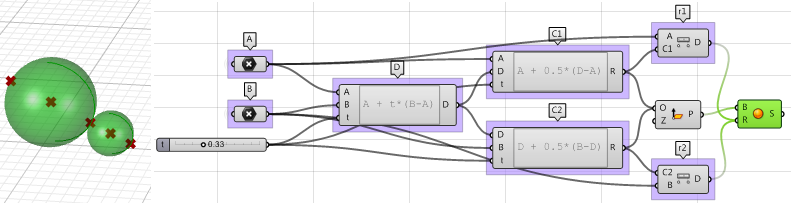
1. Utilisez le composant Expression pour définir le point $$D$$ entre $$A$$ et $$B$$ au niveau d’un paramètre $$t$$. L’expression que nous utiliserons est basée sur l’équation vectorielle d’une ligne :
$$D = A + t*(B-A)$$$$B-A$$ est le vecteur qui va du point $$A$$ au point $$B$$ en utilisant l’opération de soustraction de vecteurs.
$$t*(B-A)$$ : où $$t$$ se trouve entre 0 et 1 pour obtenir une position sur le vecteur.
$$A+t*(B-A)$$ : donne un point sur le vecteur entre A et B.
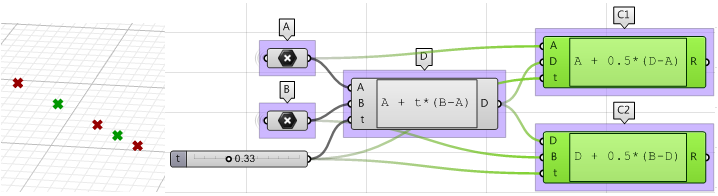
2. Utilisez le composant Expression pour définir également les milieux $$C1$$ et $$C2$$.
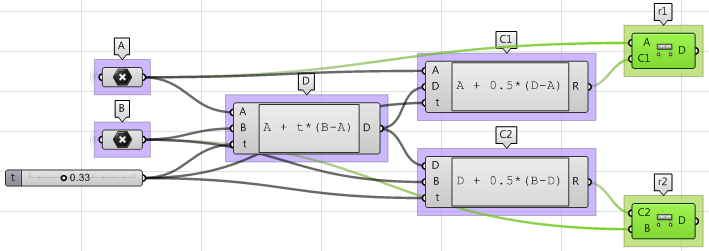
3. Le rayon de la première sphère $$(r1)$$ et le rayon de la deuxième sphère $$(r2)$$ peuvent être calculés en utilisant le composant Distance.
4. L’étape finale consiste à créer la sphère à partir d’un plan de base et d’un rayon. Nous devons vérifier que les origines sont verrouillées sur $$C1$$ et $$C2$$ et les rayons sur $$r1$$ et $$r2$$.
En utilisant le composant VB de Grasshopper :
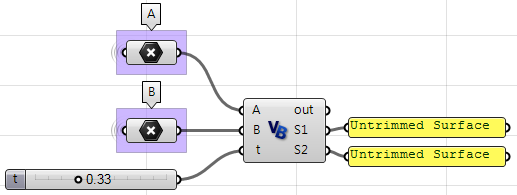
Private Sub RunScript(ByVal A As Point3d, ByVal B As Point3d, ByVal t As Double, ByRef S1 As Object, ByRef S2 As Object)
'declare variables
Dim D, C1, C2 As Rhino.Geometry.Point3d
Dim r1, r2 As Double
'find a point between A and B
D = A + t * (B - A)
'find mid point between A and D
C1 = A + 0.5 * (D - A)
'find mid point between D and B
C2 = D + 0.5 * (B - D)
'find spheres radius
r1 = A.DistanceTo(C1)
r2 = B.DistanceTo(C2)
'create spheres and assign to output
S1 = New Rhino.Geometry.Sphere(C1, r1)
S2 = New Rhino.Geometry.Sphere(C2, r2)
End Sub
En utilisant le composant Python :
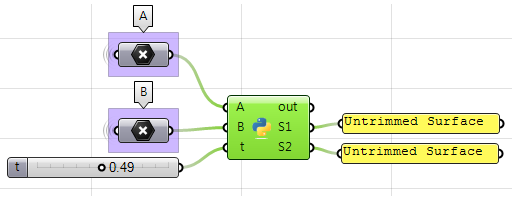
import Rhino
#find a point between A and B
D = A + t * (B - A)
#find mid point between A and D
C1 = A + 0.5 * (D - A)
#find mid point between D and B
C2 = D + 0.5 * (B - D)
#find spheres radius
r1 = A.DistanceTo(C1)
r2 = B.DistanceTo(C2)
#create spheres and assign to output
S1 = Rhino.Geometry.Sphere(C1, r1)
S2 = Rhino.Geometry.Sphere(C2, r2)
En utilisant le composant C# de Grasshopper :
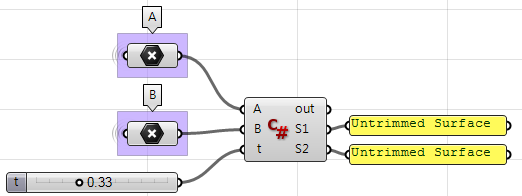
private void RunScript(Point3d A, Point3d B, double t, ref object S1, ref object S2)
{
//declare variables
Rhino.Geometry.Point3d D, C1, C2;
double r1, r2;
//find a point between A and B
D = A + t * (B - A);
//find mid point between A and D
C1 = A + 0.5 * (D - A);
//find mid point between D and B
C2 = D + 0.5 * (B - D);
//find spheres radius
r1 = A.DistanceTo(C1);
r2 = B.DistanceTo(C2);
//create spheres and assign to output
S1 = new Rhino.Geometry.Sphere(C1, r1);
S2 = new Rhino.Geometry.Sphere(C2, r2);
}
Téléchargement de fichiers d’exemple
Téléchargez le fichier Fondements mathématiques, qui contient tous les exemples de Grasshopper et les fichiers de code de ce guide.
Étapes suivantes
Maintenant que vous avez vu les mathématiques vectorielles, consultez le guide Matrices et transformations pour en apprendre davantage sur le déplacement, la rotation et la mise à l’échelle des objets.

