6.1 My Favorite Things
We’ve already been using arrays in examples and I’ve always told you not to worry about it. Those days are officially over. Now is the time to panic. Perhaps it’s best if we just get the obvious stuff out of the way first:
An array is a list of variables
That’s really all there is to it. Sometimes -in fact quite often- you want to store large or unknown amounts of variables. You could of course declare 15,000 different variables by hand but that is generally considered to be bad practise. The only thing about arrays which will seem odd at first is the way they count. Arrays start counting at zero, while we are used to start counting at one. Try it by counting the number of fingers on your right hand. Chances are you are someone who has just counted to five. Arrays would disagree with you, they would only have counted to four:
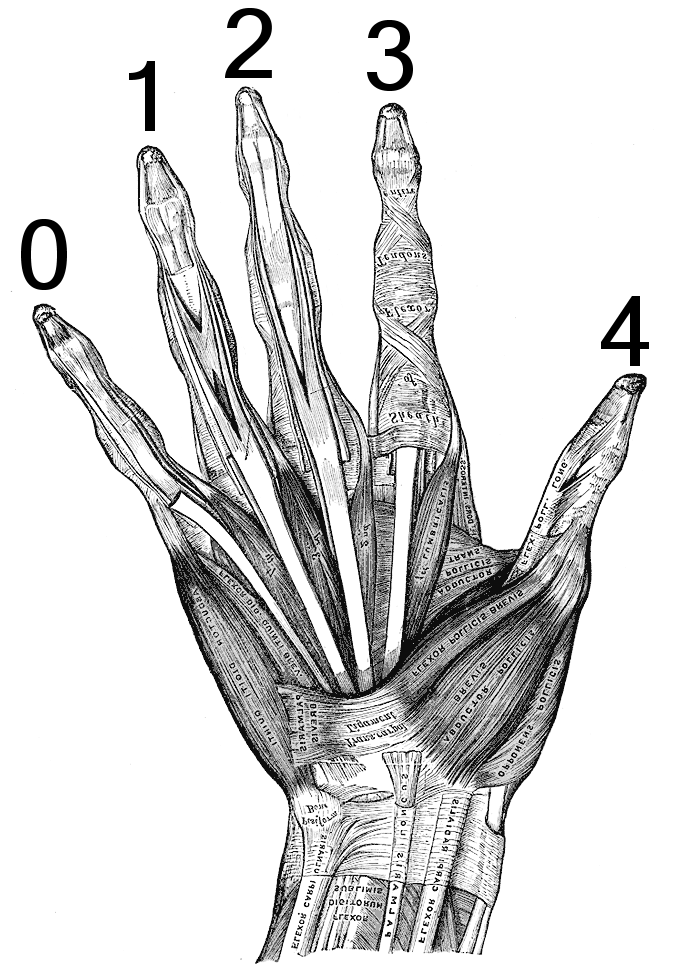
It helps to refer to numbers as ‘indices’ when you use the zero-based counting system just to avoid confusion. So when we talk about the ‘first element’ of an array, we actually mean ’the element with index 0’. I know this all sounds like Teaching Granny To Suck Eggs, but zero-based counting systems habitually confuse even the most die-hard programmer.
Arrays are just like other variables in VBScript with the exception that we have to use parenthesis to set and retrieve values:
'Normal variable declaration, assignment and retrieval
Dim intNumber
intNumber = 8
Call Rhino.Print(intNumber)
'Array declaration, assignment and retrieval
Dim arrNumbers(2)
arrNumbers(0) = 8
arrNumbers(1) = -5
arrNumbers(2) = 47
Call Rhino.Print(arrNumbers(0) & ", " & arrNumber(1) & ", " & arrNumbers(2))
The example above shows how to declare an array which is capable of storing 3 numbers (indices 0, 1 and 2). In cases like this (when you know in advance how many and which numbers you want to assign) you can also use a shorthand notation in which case you have to omit the parenthesis in the variable declaration:
Dim arrNumbers
arrNumbers = Array(8, -5, 47)
The Array() function in VBScript takes any number of variables and turns them into an array. It is a bit of an odd function since it has no fixed signature, you can add as many arguments as you like. Note that in the above example there is nothing special about the array declaration, it could be any other variable type as well.
This paragraph is called “My favourite things” not because arrays are my favourite things, but because of the example below which will teach you pretty much all there is to know about arrays except nesting:
Sub MyFavouriteThings()
Dim strPrompt, strAnswer
Dim arrThings()
Dim intCount
intCount = 0
Do
Select Case intCount
Case 0
strPrompt = "What is your most favourite thing?"
Case 1
strPrompt = "What is your second most favourite thing?"
Case 2
strPrompt = "What is your third most favourite thing?"
Case Else
strPrompt = "What is your " & (intCount+1) & "th most favourite thing?"
End Select
strAnswer = Rhino.GetString(strPrompt)
If IsNull(strAnswer) Then Exit Do
ReDim Preserve arrThings(intCount)
arrThings(intCount) = strAnswer
intCount = intCount+1
Loop
If intCount = 0 Then Exit Sub
Call Rhino.Print("Your " & UBound(arrThings)+1 & " favourite things are:")
For i = 0 To UBound(arrThings)
Call Rhino.Print((i+1) & ". " & arrThings(i))
Next
End Sub
| Line | Description |
|---|---|
| 3 | We do not know how many favourite things the user has, so there's no way we can set the array to a certain size in advance. Whenever an array is declared with parenthesis but without any number, it will be made dynamic. This means we can resize it during runtime. |
| 4...5 | We'll be using this variable for bookkeeping purposes. Although we could technically extract all information from the array itself, it's easier to keep an integer around so we can always quickly find the number of elements in the array. |
| 22 |
We've just asked the user what his/her Nth favourite thing was, and he/she answered truthfully. This means we're going to have to store the last answer in our array, but it is not big enough yet to store additional data so the first thing we must do is increase the size of *arrThings*. We can change the size (the number of possible items it can store) of an array in four different ways:
ReDim arrThings(5)
ReDim Preserve arrThings(5)
arrThings = Array(0.0, 5.8, 4.2, -0.1)
Erase arrThings
The first option will set the array to the indicated size while destroying its contents. To flog a horse which, if not at this point dead, is in mortal danger of expiring; an array with a size of five is actually capable of storing six elements (0,1,2,3,4,5). If you wish to retain the stored information -as we do in our example-, then you must add the keyword Preserve between ReDim and the array variable name. By simply assigning another array to the variable, you will also change the contents and size. This only works though if the array in question was declared without parenthesis. And finally, if you want to reset an array, you can use the Erase keyword. This will destroy all the stored data and dynamic array size will be set to zero. The array cannot contain any elements after an erase, you must first ReDim it again. If you erase a fixed size array, only the data will be destroyed. |
| 23 |
Straightforward array assignment using an index between parenthesis. If you were to try to assign a value to an array at a non-existing index you will get a fatal error:
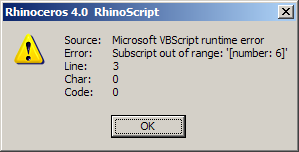
Unfortunately the message doesn’t tell us anything about which array was queried and what its size is. We do know what index generated the error ( number: 6 ). |
| 24 | We increase the bookkeeping integer since the array is now one larger than before. |
| 27 | It is possible the user has not entered any String. If this is the case the intCount variable will still have a value of zero which we assigned on line 5. There is nothing for us to do in this case and we should abort the subroutine. |
| 29 | After the loop has completed and we've made certain the array contains some actual data, we print all the gathered information to the command history. First we will tell the user how many favourite things he/she entered. We could again use the intCount variable to retrieve this information, but it is also possible to extract that data directly from the array itself using the UBound() function. UBound is short for "Upper bound", which is the terminology used to indicate the highest possible index of an array. If the array is empty the upper bound is technically -1. However, if we attempt to use the UBound() function on an array which cannot contain any elements, there will be a fatal error:
Dim arrList()
Call Rhino.Print(UBound(arrList))
The above will fail.. |
| 30 | This is a typical usage of the For…Next loop. Whenever we want to iterate through an array using index values, we use something like the following:
For i = 0 To UBound(arrData)
…
Next
It is customary to use a short variable name for iteration variables. This clashes with the prefix rules as defined on page 9 and is to be treated as a special case. Typically, for simple iteration variables i, j and k are used:
For i = 1 To UBound(arrData)
For j = 0 To i-1
For k = 0 To UBound(arrDifferentData)
…
Next
Next
Next
|
| 31 | Standard array value retrieval. |
6.2 Points and Vectors
In RhinoScript, coordinates are defined as arrays of three numbers. Element 0 corresponds with x, element 1 with y and element 2 with z. This notation is used for both points and vectors.

Sub PointSpiral()
Dim arrPoint(2)
Dim t, pi
pi = Rhino.Pi()
'Call Rhino.EnableRedraw(False)
For t = -5 To 5 Step 0.025
arrPoint(0) = t * Sin(5*t)
arrPoint(1) = t * Cos(5*t)
arrPoint(2) = t
Call Rhino.Print(Rhino.Pt2Str(arrPoint, 3))
Call Rhino.AddPoint(arrPoint)
Next
'Call Rhino.EnableRedraw(True)
End Sub
The variable arrPoint is declared as a fixed size array on line 2 and the elements are assigned different values on lines 9 to 11 inside the body of the loop. On line 13 the array is converted to a String using the RhinoScript method Rhino.Pt2Str(). Pt2Str and Str2Pt (abbreviations for PointToString and StringToPoint respectively) can be used to convert points into Strings and vice versa. The regular VBScript function CStr() for casting variables into Strings will not work on arrays and cannot be used. The additional benefit of Pt2Str is that it takes optional formatting arguments.

Vectors are a new concept in RhinoScript for Rhino4. Those of you who are familiar with the essentials of geometrical mathematics will have no problems with this concept… in fact you probably all are familiar with the essentials of geometrical mathematics or you wouldn’t be learning how to program a 3D CAD platform.
Vectors are indistinguishable from points. That is, they are both arrays of three doubles so there’s absolutely no way of telling whether a certain array represents a point or a vector. There is a practical difference though; points are absolute, vectors are relative. When we treat an array of three doubles as a point it represents a certain coordinate in space, when we treat it as a vector it represents a certain direction. You see, a vector is an arrow in space which always starts at the world origin (0.0, 0.0, 0.0) and ends at the specified coordinate.
The picture on the right shows two vector definitions; a purple and a blue one. The blue one happens to have all positive components while the purple one has only negative components. Both vectors have a different direction and a different length. When I say vectors are relative, I mean that they only indicate the difference between the start and end points of the arrow, i.e. vectors are not actual geometrical entities, they are only information. The blue vector could represent the tangent direction of the black curve at parameter {t}. If we also know the point value of the curve at parameter {t}, we know what the tangent of the curve looks like; we know where in space the tangent belongs. The vector itself does not contain this information; the orange and the blue vector are identical in every respect.
The addition of vector definitions in RhinoScript is accompanied by a whole group of point/vector related methods which perform the basic operations of ‘vector mathematics’. Addition, subtraction, multiplication, dot and cross products and so on and so forth. The table on the following page is meant as a reference table, do not waste your time memorizing it.
I will be using standard mathematical notation:
- A lowercase letter represents a number
- A lowercase letter with a dot above it represents a point
- A lowercase letter with an arrow above it represents a vector
- Vertical bars are used to denote vector length
| Notation | Implementation | Description | Example |
|---|---|---|---|
| $$d =|\dot{p}-\dot{r}|$$ | Distance(Pt1, Pt2) | Compute the distance between two points. |  |
| $$\dot{r} = a \times \dot{p}$$ | PointScale(Pt1, dblA) | Multiply the components of the point by the specified factor. This operation is the equivalent of a 3DScaling around the world origin. |  |
| $$\dot{r} = \frac{\dot{p}}{a}$$ | PointDivide(Pt1, dblA) | Divide the components of the point by the specified factor. This is the equivalent of PointScale(Pt1, a-1). |  |
| $$? \dot{r} = \dot{p} \pm t$$ | PointCompare(Pt1, Pt2, dblT) | Check to see if two points are more or less identical. Two points are identical if the length of the vector between them is less than the specified tolerance. |  |
| $$\dot{r} = \dot{p} \times \mathbb{M}$$ | PointTransform(Pt1, arrM) | Transform the point using a linear transformation matrix. |  |
| $$\overrightarrow{w} = \left(\frac{1}{|\overrightarrow{v}|} \right) \times \overrightarrow{v}$$ | VectorUnitize(Vec1) | Divide all components by the inverse of the length of the vector. The resulting vector has a length of 1.0 and is called the unit-vector. Unitizing is sometimes referred to as "normalizing". |  |
| $$l = |\overrightarrow{v}|$$ | VectorLength(Vec1) | Compute the square root of the sum of the squares of all the components. Standard Pythagorean distance equation. |  |
| $$\overrightarrow{w} = -\overrightarrow{v}$$ | VectorReverse(Vec1) | Negate all the components of a vector to invert the direction. The length of the vector is maintained. |  |
| $$? \overrightarrow{w} = \overrightarrow{v} \pm t$$ | VectorCompare(Vec1, Vec2, dblT) | Check to see if two vectors are more or less identical. This is the equivalent of PointCompare(). |  |
| $$\overrightarrow{w} =\frac{\overrightarrow{v}}{a}$$ | VectorDivide(Vec1, dblA) | Divide the components of the vector by the specified factor. This is the equivalent of *PointDivide()*. |  |
| $$\dot{r} = \dot{p} + \overrightarrow{v}$$ | PointAdd(Pt1, Vec1) | Add the components of the vector to the components of the point. Point-Vector summation is the equivalent of moving the point along the vector. |  |
| $$\dot{r} = \dot{p} - \overrightarrow{v}$$ | PointSubtract(Pt1, Vec1) | Subtract the components of the vector from the components of the point. Point-Vector subtraction is the equivalent of moving the point along the reversed vector. |  |
| $$\overrightarrow{v} = \dot{p} - \dot{r}$$ | PointSubtract(Pt1, Vec1) | Subtract the components of the vector from the components of the point. Point-Vector subtraction is the equivalent of moving the point along the reversed vector. |  |
| $$\overrightarrow{u} = \overrightarrow{v} + \overrightarrow{w}$$ | VectorAdd(Vec1, Vec2) | Add the components of Vec1 to the components of Vec2. This is equivalent to standard vector summation. |  |
| $$\overrightarrow{u} = \overrightarrow{v} - \overrightarrow{w}$$ | VectorSubtract(Vec1, Vec2) | Subtract the components of Vec1 from the components of Vec2. This is equivalent of *VectorAdd(Vec1, -Vec2)*. |  |
| $$\alpha = \overrightarrow{v} \times \overrightarrow{w}$$ | VectorDotProduct(Vec1, Vec2) -or- VectorMultiply(Vec1, Vec2) |
Calculate the sum of the products of the corresponding components. In practical, everyday-life the DotProduct can be used to compute the angle between vectors since the DotProduct of two vectors v and w equals: |v||w| cos(a) |  |
| $$\overrightarrow{u} = \overrightarrow{v} \times \overrightarrow{w}$$ | VectorCrossProduct(Vec1, Vec2) | The cross-product of two vectors v and w, is a third vector which is perpendicular to both v and w. |  |
| $$\overrightarrow{u} = \overrightarrow{v} \times (\sphericalangle\alpha)\overrightarrow{w}$$ | VectorRotate(Vec1, dblA, VecA) | Rotate a vector a specified number of degrees around an axis-vector. |  |
You probably feel like you deserved a break by now. It’s not a bad idea to take a breather before we dive into the next example of vector mathematics. Not that the math is difficult, it’s actually a lot easier than the above table would lead you to believe. In fact, it is so laughingly easy I thought it a good idea to add something extra…
RhinoScript has no method for displaying vectors which is a pity since this would be very useful for visual feedback. I shall define a function here called AddVector() which we will use in examples to come. The function must be able to take two arguments; one vector definition and a point definition. If the point array is not defined the vector will be drawn starting at the world origin. Since this is a function which we will be using extensively we must make sure it is absolutely fool-proof. This is not an easy task since it could potentially choke on eleven different culprits. I’m not going to spell them all out since we’ll be using a naughty trick to prevent this function from crashing.

Function AddVector(ByVal vecDir, ByVal ptBase)
On Error Resume Next
AddVector = Null
If IsNull(ptBase) Or Not IsArray(ptBase) Then
ptBase = Array(0,0,0)
End If
Dim ptTip
ptTip = Rhino.PointAdd(ptBase, vecDir)
If Not (Err.Number = 0) Then Exit Function
AddVector = Rhino.AddLine(ptBase, ptTip)
If Not (Err.Number = 0) Then Exit Function
If IsNull(AddVector) Then Exit Function
Call Rhino.CurveArrows(AddVector, 2)
End Function
| Line | Description |
|---|---|
| 1 | Standard function declaration. The function takes two arguments, if the first one does not represent a proper vector array the function will not do anything, if the second one does not represent a proper point array the function will draw the vector from the world origin. |
| 2 | This is the naughty bit. Instead of checking all the variables for validity we'll be using the VBScript error object. The On Error Resume Next statement will prevent the function from generating a run-time error when things start to go pear-shaped. Instead of aborting (crashing) the entire script it will simply march on, trying to make the best of a bad situation. We can still detect whether or not an error was generated and suppressed by reading the Number property of the Err object.
Using the On Error Resume Next statement will reset the error object to default values. |
| 3 | Right now we're assigning the Null value to the function in case we need to abort prematurely. We want our function to either return a valid object ID on success or Null on failure. If we simply call the Exit Function statement before we assign anything to the AddVector variable, we will return a vbEmpty value which is the default for all variables. |
| 5..7 | In case the ptBase argument does not represent an array, we want to use the world origin instead. |
| 9...10 | Declare and compute the coordinate of the arrow tip. This will potentially fail if ptBase or vecDir are not proper arrays. However, the script will continue instead of crash due to the error trapping. |
| 11 | Since we just passed a dangerous bump in the code, we have to check the value of the error number. If it is still zero, no error has occurred and we're save to continue. Otherwise, we should abort. |
| 13 | Here we are calling the RhinoScript method Rhino.AddLine() and we're storing the return value
directly into the AddVector variable. There are three possible scenarios at this point:
In the case of scenario 1, the AddVector variable now contains the object ID for a newly added line object. This is exactly what we want the function to return on success. In case of scenario #2, the AddVector will be set to Null. Of course it already was Null, so nothing actually changed. The last option means that there was no return value for AddLine() and hence AddVector will also be Null. But the error-number will contain a non-zero value now. |
| 14...15 | Check for scenario 2 and 3, abort if we find either one of them occurred. |
| 17 | Add an arrow-head to the line object. |
| 18 | Complete the function declaration. Once this line is executed the value of AddVector will be returned, whatever it is. |
6.3 An AddVector() Example

Option Explicit
'This script will compute a bunch of cross-product
vector based on a pointcloud
VectorField()
Sub VectorField()
Dim strCloudID
strCloudID = Rhino.GetObject("Input pointcloud", 2, True, True)
If IsNull(strCloudID) Then Exit Sub
Dim arrPoints : arrPoints = Rhino.PointCloudPoints(strCloudID)
Dim ptBase : ptBase = Rhino.GetPoint("Vector field base point")
If IsNull(ptBase) Then Exit Sub
Dim i
For i = 0 To UBound(arrPoints)
Dim vecBase
vecBase = Rhino.VectorCreate(arrPoints(i), ptBase)
Dim vecDir : vecDir = Rhino.VectorCrossProduct(vecBase, Array(0,0,1))
If Not IsNull(vecDir) Then
vecDir = Rhino.VectorUnitize(vecDir)
vecDir = Rhino.VectorScale(vecDir, 2.0)
Call AddVector(vecDir, arrPoints(i))
End If
Next
End Sub
| Line | Description |
|---|---|
| 10a | We can use the colon to make the interpreter think that one line of code is actually two. Stacking lines of code like this can severely damage the readability of a file, so don't be overzealous. Personally, I only use colons to combine variable declaration/assignment on one line. |
| 10b | The arrPoints variable is an array which contains all the coordinates of a pointcloud object. This is an example of a nested array (see paragraph 6.4). |
| 17 | arrPoints(i) contains an array of three doubles; a standard Rhino point definition. We use that point to construct a new vector definition which points from the Base point to arrPoints(i). |
| 19 | The Rhino.VectorCrossProduct() method will return a vector which is perpendicular to vecBase and the world z-axis. If you feel like doing some homework, you can try to replace the hard-coded direction (Array(0,0,1)) with a second variable point a la ptBase. |
| 21 | Rhino.VectorCrossProduct() will fail if one of the input vectors is zero-length or if both input vectors are parallel. In those cases we will not add a vector to the document. |
| 22...23 | Here we make sure the vecDir vector is two units long. First we unitize the vector, making it one unit long, then we double the length.. |
| 25 | Finally, place a call to the AddVector() function we defined on page 40. If you intend to run this script, you must also include the AddVector() function in the same script. |
6.4 Nested Lists
I wonder why, I wonder why.
I wonder why I wonder.
I wonder why I wonder why.
I wonder why I wonder.
-Richard P. Feynman-

Before we begin with nested arrays we need to take care of some house- keeping first:
Nested arrays are not the same as two-dimensional arrays. Up to and including Rhino2, point lists in RhinoScript were stored in two-dimensional arrays. This system was changed to nested arrays in Rhino3. The only methods which still use two-dimensional arrays are the intersection and matrix methods.
Now then, nested arrays. There’s nothing to it. An array becomes nested when it is stored inside another array. The VectorField example on the previous page deals with an array of points (an array of arrays of three doubles). The image on the right is a visualization of such a structure. The left most column represents the base array, the one containing all coordinates. It can be any size you like, there’s no limit to the amount of points you can store in a single array. Every element of this base array is a standard Rhino point array. In the case of point-arrays all the nested arrays are three elements long, but this is not a requisite, you can store anything you want into an array.
Accessing nested arrays follows the same rules as accessing regular arrays. Using the VectorField example:
Dim arrSeventhPoint, arrLastPoint
arrSeventhPoint = arrPoints(6)
arrLastPoint = arrPoints(UBound(arrPoints))
This shows how to extract entire nested arrays. Assuming the illustration on this page represents arrPoints, arrSeventhPoint will be identical to Array(0.3, -1.5, 4.9). If we want to access individual coordinates directly we can stack the indices:
Dim dblSeventhPointHeight
dblSeventhPointHeight = arrPoints(6)(2)
The above code will store the third element of the nested array stored in the seventh element of the base array in dblSeventhPointHeight. This corresponds with the orange block.
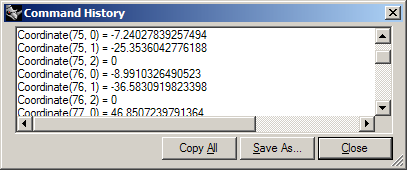
Nested arrays can be parsed using nested loops like so:
Dim i, j
For i = 0 To UBound(arrPoints)
For j = 0 To 2
Call Rhino.Print("Coordinate(" & i & ", " & j & ") = " & arrPoints(i)(j))
Next
Next
Remember the scaling script from page 31? We’re now going to take curve-length adjustment to the next level using nested arrays. The logic of this script will be the same, but the algorithm for shortening a curve will be replaced with the following one (the illustration shows the first eight iterations of the algorithm):

Every control-point or ‘vertex’ of the original curve (except the ones at the end) will be averaged with its neighbours in order to smooth the curve. With every iteration the curve will become shorter and we will abort as soon a certain threshold length has been reached. The curve can never become shorter than the distance between the first and last control-point, so we need to make sure our goals are actually feasible before we start a potentially endless loop. Note that the algorithm is approximating, it may not be endless but it could still take a long time to complete. We will not support closed or periodic curves.
We’re going to put the vector math bit in a separate function. This function will compute the {vM} vector given the control points {pN-1; p; pN+1} and a smoothing factor {s}. Since this function is not designed to fail, we will not be adding any error checking, if the thing crashes we’ll have to fix the bug. Instead of using VBScript variable naming conventions, I’ll use the same codes as in the diagram:
Function SmoothingVector(ByVal P, ByVal Pprev, ByVal Pnext, ByVal s)
Dim Pm(2), i
For i = 0 To 2
Pm(i) = (Pprev(i) + Pnext(i)) / 2.0
Next
Dim Va, Vm
Va = Rhino.VectorCreate(Pm, P)
Vm = Rhino.VectorScale(Va, s)
SmoothingVector = Vm
End Function
| Line | Description |
|---|---|
| 4..6 | We'll use this loop to iterate through all the coordinates in the point arrays. |
| 5 | Compute the average value of the two components. {pm} is the halfway point between {pprev} and {pnext}. |
| 9 | Create the {va} vector. |
| 10 | Depending on the value of {s}, the smoothing will occur quickly or slowly. When {s} has a value of 1.0, it will have no effect on the algorithm since {vM} will be the same length as {vA}. Values higher than 1.0 are likely to make the smoothing operation overshoot. A value of 0.0 will stop the smoothing from taking place at all since {vM} will become a zero-length vector. Values lower than 0.0 will invert the smoothing.
When we use this algorithm, we must make sure to set s to be something sensible, or the loop might become endless: 0.0 1 {s} # 1.0 |
We’ll also put the entire curve-smoothing algorithm in a separate function. Since it’s fairly hard to adjust existing objects in Rhino, we’ll be adding a new curve and deleting the existing one:
Function SmoothCurve(ByVal strCurveID, ByVal s)
Dim arrCP : arrCP = Rhino.CurvePoints(strCurveID)
Dim arrNewCP : arrNewCP = arrCP
Dim i
For i = 1 To UBound(arrCP) - 1
Dim Vm
Vm = SmoothingVector(arrCP(i), arrCP(i-1), arrCP(i+1), s)
arrNewCP(i) = Rhino.PointAdd(arrCP(i), Vm)
Next
Dim arrKnots : arrKnots = Rhino.CurveKnots(strCurveID)
Dim intDegree : intDegree = Rhino.CurveDegree(strCurveID)
Dim arrWeights: arrWeights = Rhino.CurveWeights(strCurveID)
SmoothCurve = Rhino.AddNurbsCurve(arrNewCP, arrKnots, intDegree, arrWeights)
If IsNull(SmoothCurve) Then Exit Function
Call Rhino.DeleteObject(strCurveID)
End Function
| Line | Description |
|---|---|
| 2 | Retrieve the nested array of curve control points. |
| 3 | We'll need a copy of the arrCP array since we need to create a new array for all the smoothed points while keeping the old array intact. |
| 6 | This loop will start at one and stop one short of the upper bound of the array. In other words, we're skipping the first and last items in the array. |
| 8 | Compute the smoothing vector using the current control point, the previous one (i-1) and the next one (i+1). Since we're omitting the first and last point in the array, every point we're dealing with has two neighbours. |
| 9 | Set the new control point position. The new coordinate equals the old coordinate plus the smoothing vector. |
| 12...14 | We'll be adding a new curve to the document which is identical to the existing one, but with different control point positions. A nurbs curve is defined by four different blocks of data: control points, knots, weights and degree (see paragraph 7.7 Nurbs Curves). We just need to copy the other bits from the old curve. |
| 16 | Create a new nurbs curve and store the object ID in the function variable. |
| 19 | Delete the original curve. |
The top-level subroutine doesn’t contain anything you’re not already familiar with:
Sub IterativeShortenCurve()
Dim strCurveID : strCurveID = Rhino.GetObject("Open curve to smooth", 4, True)
If IsNull(strCurveID) Then Exit Sub
If Rhino.IsCurveClosed(strCurveID) Then Exit Sub
Dim dblMin, dblMax, dblGoal
dblMin = Rhino.Distance(Rhino.CurveStartPoint(strCurveID), Rhino.CurveEndPoint(strCurveID))
dblMax = Rhino.CurveLength(strCurveID)
dblGoal = Rhino.GetReal("Goal length", 0.5*(dblMin + dblMax) , dblMin, dblMax)
If IsNull(dblGoal) Then Exit Sub
Do Until Rhino.CurveLength(strCurveID) < dblGoal
Call Rhino.EnableRedraw(False)
strCurveID = SmoothCurve(strCurveID, 0.1)
If IsNull(strCurveID) Then Exit Do
Call Rhino.EnableRedraw(True)
Loop
End Sub
Next Steps
Array are very powerful in RhinoScript. Let’s make a quick stop to learn about geometry objects.

