Le trasformazioni fanno riferimento a operazioni come lo spostamento (chiamato anche traduzione), la rotazione e la scalatura di oggetti. Queste operazioni vengono archiviate nella programmazione 3D usando matrici che non sono altro che serie rettangolari di numeri. È possibile eseguire varie trasformazioni molto velocemente usando le matrici. Una matrice [4x4] può rappresentare tutte le trasformazioni. È possibile ridurre i tempi di calcolo usando dimensioni della matrice unificate.
$$\begin{array}{rcc} \mbox{matrix}&\begin{array}{cccc} c1& c2&c3&c4\end{array}\\\begin{array}{c}row(1)\\row(2)\\row(3)\\row(4)\end{array}& \left[\begin{array}{cr} +&+&+&+\\ +&+&+&+\\ +&+&+&+\\ +&+&+&+\end{array}\right] \end{array}$$2.1 Operazioni con le matrici
In grafica digitale, l’operazione più importante è il prodotto fra matrici, un concetto che spiegheremo nel con qualche dettaglio.
Prodotto fra matrici
Il prodotto fra matrici viene usato per applicare trasformazioni alla geometria. Ad esempio, se abbiamo un punto e vogliamo ruotarlo su un asse, usiamo una matrice di rotazione moltiplicandola per il punto, in modo da ottenere una nuova posizione ruotata.
$$\begin{array}{ccc} \text{rotate matrix} & \text{input point} & \text{rotate point}\\\begin{bmatrix}a & b & c & d \\e & f & g & h \\i & j & k & l \\0 & 0 & 0 & 1 \\\end{bmatrix}& \cdot\begin{bmatrix}x \\y\\z\\1 \\\end{bmatrix}&= \begin{bmatrix}x' \\y'\\z'\\1 \\\end{bmatrix}\end{array}$$La maggior parte del tempo, occorre eseguire varie trasformazioni sulla stessa geometria. Ad esempio, se dobbiamo spostare e ruotare migliaia di punti, possiamo usare uno dei seguenti metodi.
Metodo 1
- Moltiplicare la matrice di spostamento per 1000 punti in modo da spostare i punti.
- Moltiplicare la matrice di rotazione per i 1000 punti risultanti in modo da ruotare i punti spostati.
Numero di operazioni = 2000.
Metodo 2
- Moltiplicare le matrici di spostamento e di rotazione per creare una matrice di trasformazioni combinata.
- Moltiplicare la matrice combinata per 1000 punti in modo da spostarla e ruotarla in un solo passaggio.
Numero di operazioni = 1001.
Nota: il metodo 1 menzionato implica quasi il doppio delle operazioni per ottenere lo stesso risultato. Il metodo 2 è molto efficiente, ma è possibile solo se entrambe le matrici di spostamento e rotazione sono $$[4 \times 4]$$. Ciò è dovuto al fatto che in computer grafica, una matrice $$[4 \times 4]$$viene utilizzata per rappresentare tutte le trasformazioni mentre una matrice $$[4 \times 1]$$ è usata per rappresentare punti.
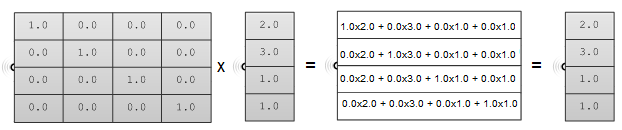
Le applicazioni di modellazione tridimensionali forniscono strumenti per applicare trasformazioni e moltiplicare matrici, ma mostreremo un semplice esempio sul processo di moltiplicazione delle matrici per gli utenti interessati a questo argomento. Per moltiplicare due matrici, queste devono presentare dimensioni coincidenti. Ciò vuol dire che il numero di colonne della prima matrice deve essere uguale al numero di righe della seconda matrice. La matrice risultante presenta dimensioni uguali al numero di righe della prima matrice e il numero di colonne della della seconda matrice. Ad esempio, se abbiamo due matrici, $$M$$ e $$P$$, con dimensioni pari rispettivamente a $$[4\times 4]$$ e $$[4 \times 1]$$, allora la matrice di moltiplicazione risultante $$M · P$$ ha una dimensione pari a $$[4 \times 1]$$ come mostrato nella figura seguente:
$$\begin{array}{ccc} M & P & P' \\\begin{bmatrix}\color{red}{a} & \color{red}{b} & \color{red}{c} & \color{red}{d} \\e & f & g & h \\i & j & k & l \\0 & 0 & 0 & 1 \\\end{bmatrix}& \cdot\begin{bmatrix}\color{red}{x} \\\color{red}{y} \\\color{red}{z} \\\color{red}{1} \\\end{bmatrix}&= \begin{bmatrix}\color{red}{x'=a*x+b*y+c*z+d*1}\\y'=e*x+f*y+g*z+h*1\\z'=i*x+j*y+k*z+l*1 \\1=0*x+0*y+0*z+1*1\\\end{bmatrix}\end{array}$$Matrice identità
La matrice identità è una matrice speciale in cui tutti gli elementi diagonali sono uguali a 1 e gli altri uguali a 0.
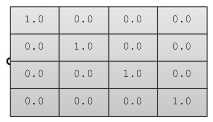
Se la matrice identità viene moltiplicata per una qualsiasi altra matrice, i valori moltiplicati per zero non cambiano; questa è la proprietà principale della matrice identità.
2.2 Operazioni di trasformazione
La maggior parte delle trasformazioni conservano il rapporto parallelo tra le parti della geometria. Ad esempio, i punti colineari rimangono tali dopo la trasformazione. Anche i punti su un piano rimangono coplanari dopo la trasformazione. Questo tipo di trasformazione viene chiamata trasformazione affine.
Trasformazione di traduzione (spostamento)
Lo spostamento di un punto da una posizione iniziale mediante un vettore può essere calcolato come di seguito:
$$P’ = P + \mathbf{\vec v}$$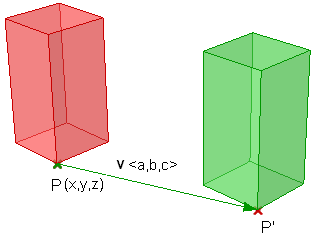
Supponiamo che:
$$P(x,y,z)$$ è un punto dato.
$$\mathbf{\vec v}=<a,b,c>$$ è un vettore di traduzione.
Allora:
$$P’(x) = x + a$$
$$P’(y) = y + b$$
$$P’(z) = z + c$$
I punti sono rappresentati nel formato di una matrice usando una matrice [4x1] con 1 inserita nell’ultima riga. Ad esempio, il punto P(x,y,z) viene rappresentato come segue:
$$\begin{bmatrix}x\\y\\z\\1\\\end{bmatrix}$$Utilizzare una matrice $$[4 \times 4]$$ per le trasformazioni (chiamato sistema di coordinate omogeneo), anziché una matrice $$[3 \times 3]$$ , consente di rappresentare tutte le trasformazioni inclusa la traduzione. Il formato generale per una matrice di traduzione è:
$$\begin{bmatrix}1 & 0 & 0 & \color{red}{a1} \\0 & 1 & 0 & \color{red}{a2} \\0 & 0 & 1 & \color{red}{a3} \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Ad esempio, per spostare il punto $$P(2,3,1)$$ mediante il vettore $$\vec v <2,2,2>$$, la nuova posizione del punto è:
$$P’ = P + \mathbf{\vec v} = (2+2, 3+2, 1+2) = (4, 5, 3)$$Se utilizziamo una forma di matrice e moltiplichiamo la matrice di traduzione per il punto di input, otteniamo la nuova posizione del punto, come mostrato di seguito:
$$\begin{bmatrix}1 & 0 & 0 & 2 \\0 & 1 & 0 & 2 \\0 & 0 & 1 & 2 \\0 & 0 & 0 & 1 \\\end{bmatrix}\cdot\begin{bmatrix}2 \\3\\1\\1 \\\end{bmatrix}= \begin{bmatrix}(1*2 + 0*3 + 0*1 + 2*1) \\(0*2 + 1*3 + 0*1 + 2*1)\\(0*2 + 0*3 + 1*1 + 2*1)\\(0*2 + 0*3 + 0*1 + 1*1)\\\end{bmatrix}=\begin{bmatrix}4 \\5\\3\\1 \\\end{bmatrix}$$Analogamente, qualsiasi geometria viene tradotta moltiplicandone i punti di costruzione per la matrice di traduzione. Ad esempio, se abbiamo un parallelepipedo definito da otto vertici e vogliamo spostarli in 4 unità nella direzione x, 5 unità nella direzione y e 3 unità nella direzione z, per ottenere il nuovo parallelepipedo, dobbiamo moltiplicare ciascuno degli otto vertici per la seguente matrice di traduzione.
$$\begin{bmatrix}1 & 0 & 0 & 4\\ 0 & 1 & 0 & 5 \\0 & 0 & 1 & 3 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$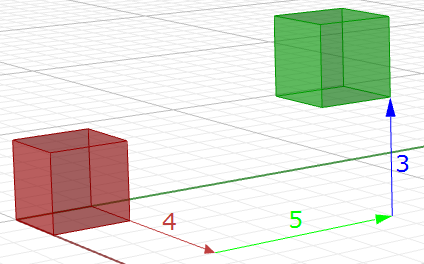
Trasformazione di rotazione
Questa sezione mostra come calcolare la rotazione attorno all’asse z e il punto di origine usando la trigonometria, quindi dedurre il formato della matrice generale per la rotazione.
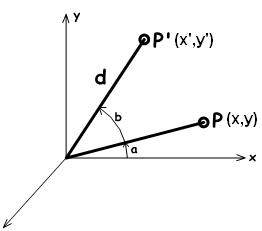
Prendere un punto sul $$x,y$$ piano $$P(x,y)$$ e ruotarlo dall’angolo( $$b$$). Osservando la figura, possiamo affermare quanto segue:
$$x = d cos(a)$$ (1)
$$y = d sin(a)$$ (2)
$$x’ = d cos(b+a)$$ (3)
$$y’ = d sin(b+a)$$ (4)
Espandere
$$x$$’ e
$$y’$$ usando le identità trigonometriche per il seno e il coseno della somma degli angoli:
$$x’ = d cos(a)cos(b) - d sin(a)sin(b)$$ (5)
$$y’ = d cos(a)sin(b) + d sin(a)cos(b)$$ (6)
Usare Eq 1 e 2:
$$x’ = x cos(b) - y sin(b)$$
y’ = x sin(b) + y cos(b)
La matrice di rotazione attorno all’asse z appare in questo modo:
$$\begin{bmatrix}\color{red}{\cos{b}} & \color{red}{-\sin{b}} & 0 & 0 \\\color{red}{\sin{b}} & \color{red}{\cos{b}} & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$La matrice di rotazione attorno all’asse x per l’angolo $$b$$ appare in questo modo:
$$\begin{bmatrix}1 & 0 & 0 & 0 \\0 & \color{red}{\cos{b}} & \color{red}{-\sin{b}} & 0 \\0 & \color{red}{\sin{b}} & \color{red}{\cos{b}} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$La matrice di rotazione attorno all’asse y per l’angolo $$b$$ appare in questo modo:
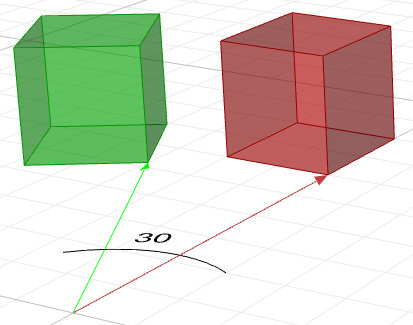
$$\begin{bmatrix}\color{red}{\cos{b}} &0 & \color{red}{\sin{b}} & 0 \\0 & 1 & 0 & 0 \\\color{red}{-\sin{b}} & 0 &\color{red}{\cos{b}} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Ad esempio, se abbiamo un parallelepipedo e vogliamo ruotarlo di 30 gradi, occorre quanto segue:
1. Costruire la matrice di rotazione di 30 gradi. Utilizzando la forma generica e i valori cos e sin di un angolo di 30 gradi, la rotazione appare in questo modo:
$$\begin{bmatrix}0.87 & -0.5 & 0 & 0 \\0.5 & 0.87 & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$2. Moltiplicare la matrice di rotazione per la geometria in input oppure, nel caso di un parallelepipedo, moltiplicare per ciascun vertice in modo da trovare la nuova posizione del parallelepipedo.
Trasformazione di scalatura
Per scalare la geometria, occorre un fattore di scala e un centro di scala. Il fattore di scala può essere una scalatura uniforme uguale nelle direzioni x, y e z oppure può essere unico per ciascun dimensione.
Per scalare un punto, è possibile usare la seguente equazione:
$$P’ = ScaleFactor(S) * P$$
Oppure:
$$P’.x = Sx * P.x$$
$$P’.y = Sy * P.y$$
$$P’.z = Sz * P.z$$
Questo è il formato della matrice per la trasformazione di scalatura, considerando il centro della scala come punto di origine del sistema di riferimento assoluto (0,0,0).
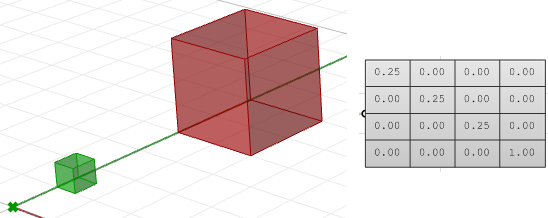
$$\begin{bmatrix}\color{red}{Scale-x} & 0 & 0 & 0 \\0 & \color{red}{Scale-y} & 0 & 0 \\0 & 0 & \color{red}{Scale-z} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}$$Ad esempio, se vogliamo scalare un parallelepipedo di 0,25 relativamente all’origine del sistema assoluto, la matrice di scalatura appare come segue:
Trasformazione di deformazione
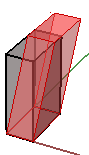
La deformazione in 3D viene misurata lungo un paio di assi relativi a un terzo asse. Ad esempio, una deformazione lungo un asse z non cambierà la geometria di tale asse, ma la modificherà lungo gli assi x e y. Ecco alcuni esempi di matrici di deformazione:
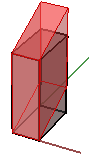
1. Deformazione negli assi x e z, mantenendo fissa la coordinata y:
$$\begin{bmatrix}1.0 &\color{red}{0.5} & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 &\color{red}{0.5} & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
2. Deformazione negli assi y e z, mantenendo fissa la coordinata x:
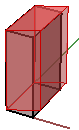$$\begin{bmatrix}1.0 & \color{red}{0.5} & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
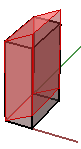$$\begin{bmatrix}1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & \color{red}{0.5} & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
3. Deformazione negli assi x e y, mantenendo fissa la coordinata z:
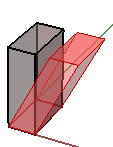$$\begin{bmatrix}1.0 & 0.0 & \color{red}{0.5} & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 \\\end{bmatrix}$$
$\begin{bmatrix}1,0 & 0 & 0 & 0,0\\ 0 & 1,0 & 0 & 0,0 \\0 & 0 & 1,0 & 0,0 \\0 & 0 & 0 & 1,0 \\\end{bmatrix}$$
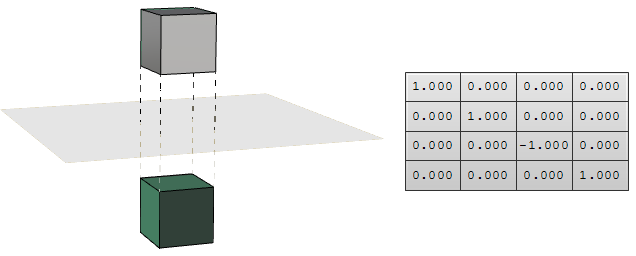
Trasformazione di riflessione
La trasformazione di riflessione crea una riflessione di un oggetto su una linea o un piano. Gli oggetti 2D vengono riflessi su una linea mentre gli oggetti 3D vengono riflessi su un piano. Occorre tener presente che la trasformazione di riflessione inverte la direzione alla normale delle facce geometriche.
trasformazione di proiezione planare
Intuitivamente, il punto di proiezione di un determinato punto 3D $$P(x,y,z)$$ su un piano xy assoluto è uguale a $$P_{xy} (x,y,0)$$ impostando il valore z su zero. Analogamente, una proiezione sul piano xz di un punto P è $$P_{xz}(x,0,z)$$. Nelle proiezioni sul piano $$P_{xz} = (0,y,z)$$. Tali proiezioni vengono definite proiezioni ortogonali.
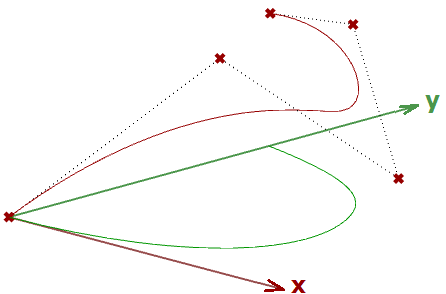
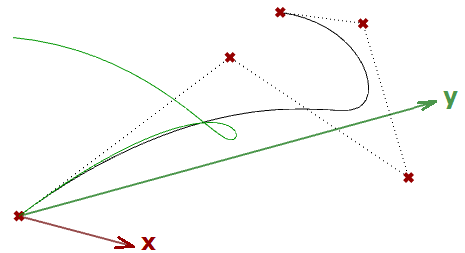
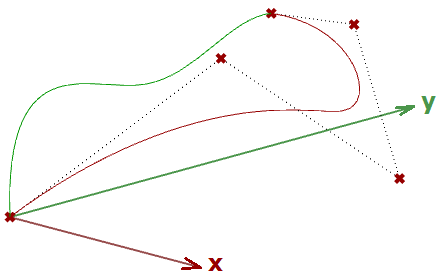
Se abbiamo una curva come input e applichiamo la trasformazione di proiezione planare, otteniamo una curva proiettata su tale piano. L’esempio seguente mostra una curva proiettata sul piano xy con il formato della matrice.
Nota: le curve NURBS (che spiegheremo nel prossimo capitolo) utilizzano punti di controllo per definire curve. Proiettare le curve per proiettarne i punti di controllo.
$\begin{bmatrix}1 & 0,0 & 0,0 & 0,0\\ 0,0 & 1 & 0,0 & 0,0 \\0,0 & 0,0 & 1 & 0,0 \\0,0 & 0,0 & 0,0 & 1 \\\end{bmatrix}$$
$\begin{bmatrix}1 & 0,0 & 0,0 & 0,0\\ 0,0 & 1 & 0,0 & 0,0 \\0,0 & 0,0 & 1 & 0,0 \\0,0 & 0,0 & 0,0 & 1 \\\end{bmatrix}$$
$\begin{bmatrix}1 & 0,0 & 0,0 & 0,0\\ 0,0 & 1 & 0,0 & 0,0 \\0,0 & 0,0 & 1 & 0,0 \\0,0 & 0,0 & 0,0 & 1 \\\end{bmatrix}$$
Download dei file di esempio
Scarica il file math-samplesandtutorials.zip, contenente tutti i file di esempio di Grasshopper e di codice di questa guida.
Passi successivi
Ora che conosci meglio le matrici e le trasformazioni, consulta la guida Curve e superfici parametriche per informazioni sulla struttura dettagliata delle curve e delle superfici NURBS.
