Supponiamo che ti sposti ogni giorno da casa al lavoro. Esci di casa alle ore 8:00 e arrivi al lavoro alle ore 9:00. Nell’intervallo dalle 8:00 alle 9:00, ti trovi in un punto del percorso. Se tracci la tua posizione ogni minuto durante il tragitto, puoi definire il percorso da casa al lavoro collegando i 60 punti tracciati. Presupponendo che ogni giorno ti sposti esattamente alla stessa velocità, alle 8:00 sei a casa (posizione iniziale), alle 9:00 arrivi al lavoro (posizione finale) e alle 8:40 ti trovi nella stessa posizione del percorso che corrisponde al quarantesimo punto tracciato. A questo punto, hai definito la tua prima curva parametrica. Hai usato il tempo come parametro per definire il percorso, quindi puoi definire la tua curva di percorso curva parametrica. L’intervallo di tempo impiegato dall’inizio alla fine (dalle 8:00 alle 9:00) viene chiamato dominio o intervallo della curva.
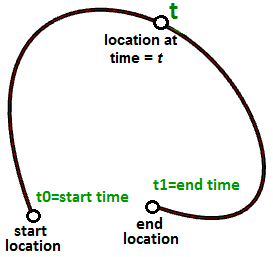
In generale, possiamo descrivere le posizioni
$$x$$,
$$y$$ e
$$z$$ di una curva parametrica in termini di parametro
$$t$$ come segue:
$$x = x(t)$$
$$y = y(t)$$
$$z = z(t)$$
Dove:
$$t$$ è un intervallo di numeri reali.
Osserviamo che l’equazione parametrica di una retta in termini del parametro $$t$$ è definita come segue:
$$x = x’ + t * a$$
$$y = y’ + t * b$$
$$z = z’ + t * c$$
Dove:
$$x$$, $$y$$ e $$z$$ sono funzioni di t dove t rappresenta un intervallo di numeri reali. $$x’$$, $$y’$$ e $$z’$$ sono le coordinate di un punto sul segmento di retta. $$a$$, $$b$$ e $$c$$ definiscono la pendenza della retta, in modo tale che il vettore $$\mathbf{\vec v} <a, b, c>$$ sia parallelo alla retta.
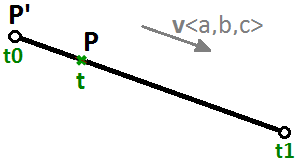
Possiamo quindi scrivere l’equazione parametrica del segmento di una retta usando un parametro $$t$$ compreso fra due valori numerici reali $$t0$$, $$t1$$ e un vettore di unità $$\mathbf{\vec v}$$ nella direzione della retta, come segue:
$$P = P’ + t * \mathbf{\vec v}$$Un altro esempio è un cerchio. L’equazione parametrica del cerchio sul piano xy, con un centro all’origine (0,0) e un parametro angolare $$t$$ compreso fra $$0$$ e $$2π$$ il radiante è:
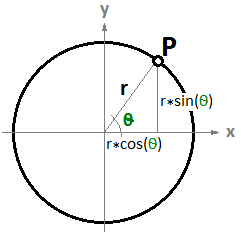
$$x = r \dot cos(t)$$
$$y = r \dot sin(t)$$
Possiamo derivare l’equazione generale di un cerchio per uno parametrico come segue:
$$ x/r = cos(t)$$
$$y/r = sin(t)$$
E poiché:
$$cos(t)^2 + sin(t)^2 = 1$$ (identità pitagorica)
Allora:
$$(x/r)^2 + (y/r)^2 = 1$$ o
$$x^2 + y^2 = r^2$$
3.1 Curve parametriche
Parametro di una curva
Un parametro su una curva rappresenta la direzione di un punto su tale curva. Come menzionato in precedenza, possiamo considerare una curva parametrica come un percorso fra due punti in un determinato intervallo di tempo, a velocità fissa o variabile. Se il tragitto impiega un determinato tempo $$T$$, allora il parametro rappresenta un tempo in $$T$$ che si traduce in una posizione (punto) sulla curva.
Se si ha un percorso rettilineo (segmento di linea) tra i due punti $$A$$ e $$B$$ e $$\mathbf{\vec v}$$ fosse un vettore da $$A$$ a $$B$$ ( $$\mathbf{\vec v} = B - A$$), è possibile utilizzare l’equazione parametrica della retta per trovare tutti i punti $$M$$ fra $$A$$ e $$B$$ come segue:
$$M = A + t*(B-A)$$
Dove:
$$t$$ è un valore compreso fra 0 e 1.
L’intervallo dei valori di t, da 0 a 1 in questo caso, si riferisce al dominio della curva o all’intervallo. Se t è un valore fuori dal dominio (inferiore a 0 o superiore a 1), allora il punto $$M$$ che ne risulta si troverà fuori dalla curva lineare $$\overline{AB}$$.
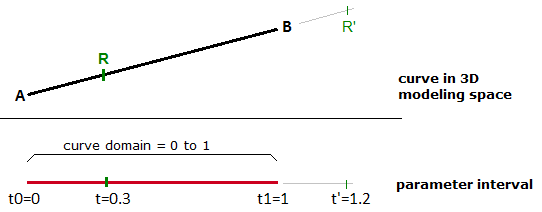
Lo stesso principio si applica a qualsiasi curva parametrica. Qualsiasi punto sulla curva può essere calcolato usando il parametro t nell’intervallo o nel dominio di valori che definiscono i limiti della curva. Il parametro iniziale del dominio viene solitamente definito come $$t0$$ e la fine del dominio come $$t1$$.
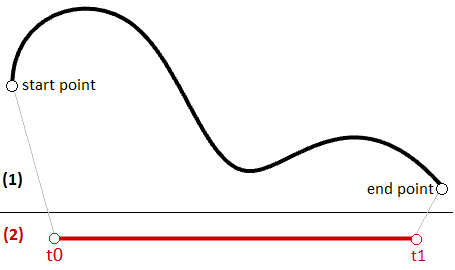
Dominio o intervallo della curva
Un dominio o intervallo della curva è definito come un intervallo di parametri considerati in un punto nella curva. Il dominio viene descritto di solito con due numeri reali, definendo i limiti del dominio espressi nella forma (da min a max) o (min, max). I limiti del dominio possono corrispondere a uno qualsiasi dei due valori correlati o non correlati alla lunghezza reale della curva. In un dominio crescente, il parametro min viene considerato il punto iniziale della curva mentre il parametro max il punto finale della curva.
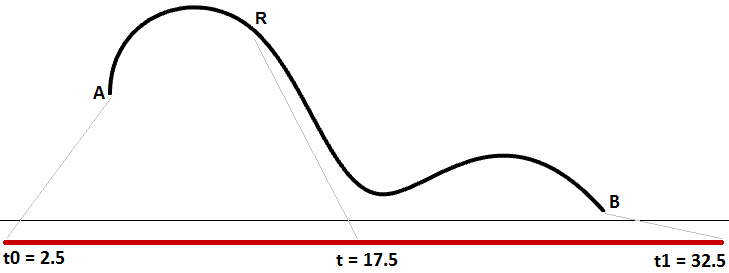
La modifica del dominio di una curva si riferisce al processo di riparametrizzazione della curva. Ad esempio, è molto comune modificare il dominio in modo che sia (da 0 a 1). La riparametrizzazione di una curva non ha effetto sulla forma della curva 3D. È come modificare il tempo di percorrenza correndo anziché camminare; anche qui la forma del percorso non cambia.
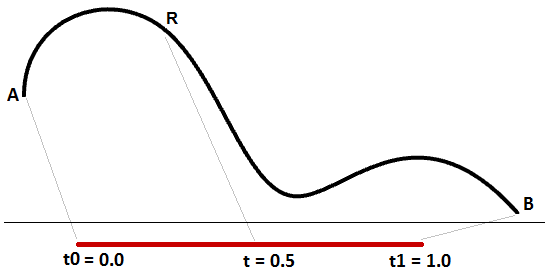
Un dominio crescente implica che il valore minimo del dominio punta verso l’inizio della curva. Di solito i domini sono crescenti, ma non sempre.
Valutazione delle curve
Abbiamo imparato che l’intervallo di una curva corrisponde all’intervallo di tutti i parametri che vengono considerati punti in una curva 3D. Tuttavia, non è possibile garantire che la valutazione al centro del dominio, ad esempio, creerà un punto che si trova al centro della curva, come mostrato nella figura (29).
Possiamo pensare alla parametrizzazione uniforme di una curva come percorso a velocità costante. Una retta di grado 1 fra due punti è un esempio in cui gli intervalli di parametri uguali si traducono in intervalli uguali della lunghezza di un arco sulla retta. Nelle curve parametriche, è raro che gli intervalli di parametri vengano considerati intervalli uguali sulla curva 3D.
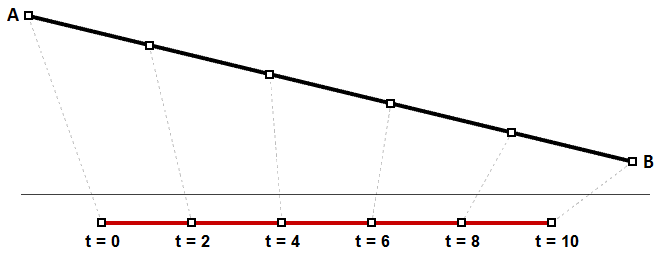
È probabile che la velocità diminuisce o aumenta lungo il percorso. Ad esempio, se per percorrere una strada impieghi 30 minuti, è improbabile che dopo 15 minuti ti trovi esattamente a metà strada. La figura (30) mostra un caso tipico in cui gli intervalli di parametri uguali vengono considerati come lunghezza variabile sulla curva 3D.
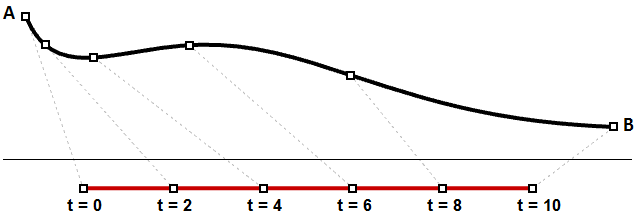
Potresti dover considerare i punti su una curva 3D impostata su una percentuale definita della lunghezza della curva. Ad esempio, potresti dover dividere la curva in lunghezze uguali. Di solito, i modellatori 3D forniscono strumenti per valutare le curve relative alla lunghezza dell’arco.
Vettore tangente a una curva
Una tangente a una curva in qualsiasi parametro (o un punto su una curva) è un vettore che tocca la curva su quel punto, ma non cambia. L’inclinazione del vettore tangente è uguale all’inclinazione della curva sullo stesso punto. Il seguente esempio valuta la tangente a una curva in due parametri diversi.
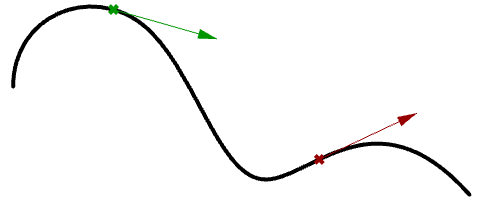
Curve polinomiali cubiche
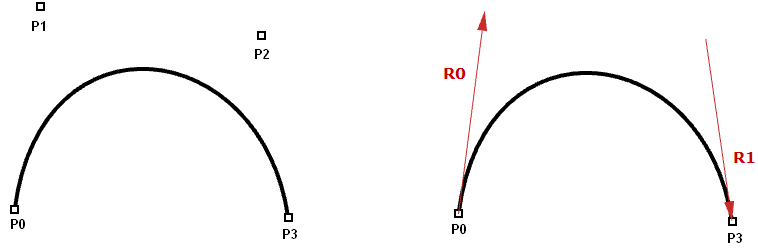
Le curve Hermite e Bézier sono due esempi di curve polinomiali cubiche determinate da quattro parametri. Un curva di Hermite è determinata da due punti di fine e due vettori tangenti a tali punti, mentre una curva di Bézier è definita da quattro punti. Sebbene i due tipi di curve siano diversi dal punto di vista matematico, condividono caratteristiche e limiti simili.
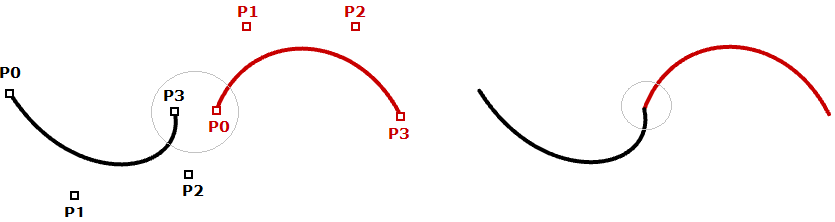
Nella maggior parte dei casi, le curve sono rappresentate da vari segmenti. Ciò richiede la creazione della cosiddetta curva cubica con funzione definita a tratti. Ecco un’illustrazione con una curva di Bézier che utilizza 7 punti di archiviazione per creare una curva cubica a due segmenti. Nota: nonostante la curva finale sia unita, non appare uniforme e continua.
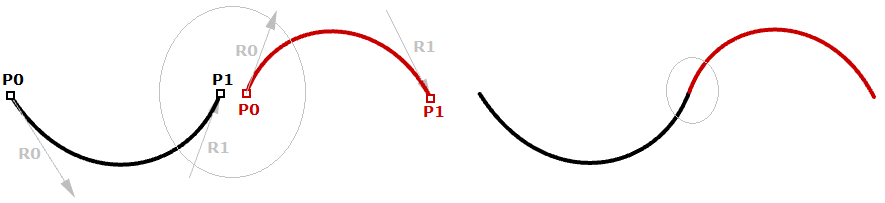
Sebbene le curve di Hermite utilizzano lo stesso numero di parametri come curve di Bézier (quattro parametri per definire una curva), offrono le informazioni aggiuntive della curva tangente, che possono anche essere condivise con il tratto successivo per creare una curva dall’aspetto uniforme con meno spazio di archiviazione totale, come mostrato di seguito.
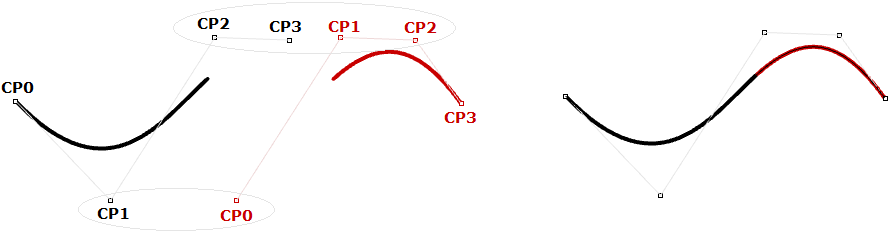
Una NURBS (Non-uniform rational B-spline) è una potente rappresentazione di curve, che mantiene curve ancora più uniformi e continue. I segmenti condividono più punti di controllo per creare curve ancora più uniformi con meno spazio di archiviazione.
Le curve e le superfici NURBS corrispondono alla principale rappresentazione matematica usata da Rhino per rappresentare la geometria. Le caratteristiche e i componenti delle curve NURBS verranno trattati nel dettaglio più avanti in questo capitolo.
Valutazione delle curve di Bézier cubiche
Dal nome del proprio inventore, Paul de Casteljau, l’algoritmo di Casteljau valuta le curve di Bézier usando un metodo ricorsivo. I passi relativi all’algoritmo possono essere riepilogati come segue:
Input:
Quattro punti $$A$$, $$B$$, $$C$$, $$D$$ definiscono una curva $$t$$$, è un qualsiasi parametro nel dominio della curva
Output:
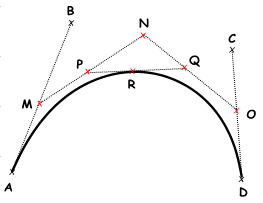
Il punto $$R$$ sulla curva che si trova sul parametro $$t$$.
Soluzione:
- Trova il punto
$$M$$ in corrispondenza del parametro
$$t$$ sulla riga
$$\overline{AB}$$.
2.Trovare il punto $$N$$ in corrispondenza del parametro $$t$$$ sulla linea $$\overline{BC}$$.
3.Trovare il punto $$O$$ in corrispondenza del parametro $$t$$$ sulla retta $$\overline{CD}$$.
4.Trovare il punto $$P$$ in corrispondenza del parametro $$t$$ sulla riga $$\overline{MN}$$.
5.Trovare il punto $$Q$$ in corrispondenza del parametro $$t$$ sulla riga $$\overline{NO}$$.
6.Trovare il punto $$R$$ in corrispondenza del parametro $$t$$ sulla riga $$\overline{PQ}$$.
3.2 Curve NURBS
La geometria NURBS è una rappresentazione matematica precisa di curve molto intuitiva e facile da modificare. È facile rappresentare curve free-form usando NURBS e la struttura di controllo semplifica e rende intuitivo il processo di modifica.
Esistono numerosi libri e bibliografia di riferimento per gli utenti interessati ad approfondire l’argomento sulla geometria NURBS. Tuttavia, è necessario conoscere i concetti di base relativi alle NURBS per poter usare i modellatori NURBS in modo più efficace. Ecco quattro attributi principali che definiscono la curva NURBS: grado, punti di controllo, nodi e regole di valutazione.
- Wikipedia: Algoritmo di De Boor.
- Michigan Tech, Department of Computer Science, De Boor’s algorithm.
Grado
Il grado della curva è un numero intero positivo. Rhino consente di lavorare con curve di qualsiasi grado iniziando da 1. I gradi 1, 2, 3 e 5 sono i più utili mentre il grado 4 e i gradi superiori a 5 non sono molto usati nel mondo reale. Di seguito, alcuni esempi di curve e il grado corrispondente:
| Linee e polilinee presentano curve NURBS di grado 1. |  |
| Cerchi ed ellissi presentano curve NURBS di grado 2. |  |
| Le curvefree-form sono di solito rappresentate come curve NURBS di grado 3 o 5. |
 |
Punti di controllo
I punti di controllo di una curva NURBS includono almeno punti di grado+1. Il modo più intuitivo di modificare la forma di una curva NURBS è spostarne i punti di controllo.
Il numero di punti di controllo che coinvolgono ciascuna suddivisione in una curva NURBS viene definito dal grado della curva. Ad esempio, ciascuna suddivisione in una curva di grado -1 è modificata solo da due punti di controllo finali. In una curva di grado -2, tre punti di controllo modificano ciascuna suddivisione e così via.
| Le curve con punti di controllo di grado 1 attraversano tutti i punti di controllo della curva. In una curva NURBS di grado 1, due punti di controllo (di grado+1) definiscono ciascuna suddivisione. Usando cinque punti di controllo, la curva presenta quattro suddivisioni. | 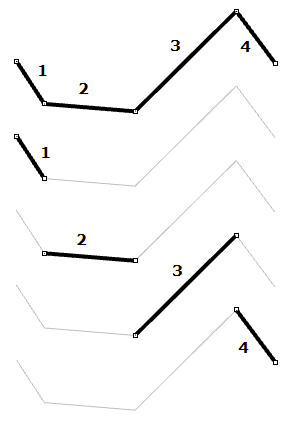 |
| I cerchi e le ellissi sono esempi di curve di grado due. In una curva NURBS di grado 2, tre punti di controllo (di grado+1) definiscono ciascuna suddivisione. Usando cinque punti di controllo, la curva presenta tre suddivisioni. | 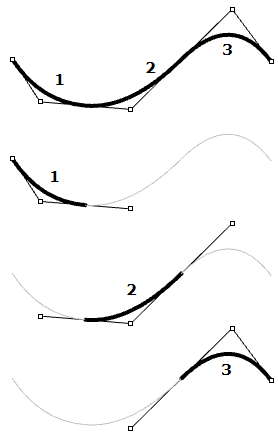 |
| Le curve con punti di controllo di grado 3 non toccano di solito la curva, ad eccezione dei punti finali in curve aperte. In una curva NURBS di grado 3, quattro punti di controllo (di grado+1) definiscono ciascuna suddivisione. Usando cinque punti di controllo, la curva presenta due suddivisioni. | 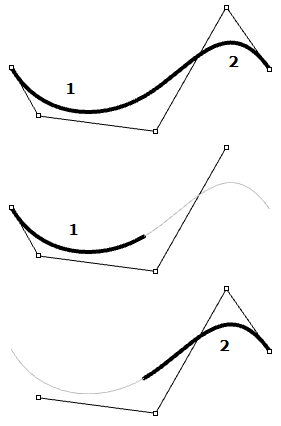 |
Pesi dei punti di controllo
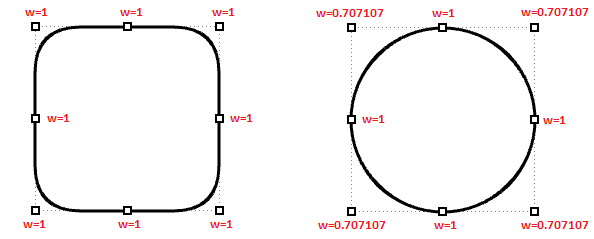
Ciascun punto di controllo ha associato un numero chiamato peso. Tranne che per alcune eccezioni, i pesi sono numeri positivi. Quando tutti i punti di controllo hanno lo stesso peso, di solito 1, la curva viene definita non razionale. Intuitivamente, possiamo considerare i pesi come la quantità di gravità di ciascun punto di controllo. Se il peso relativo di un punto di controllo è elevato, la curva viene avvicinata di più a tale punto di controllo.
Si consiglia di evitare di cambiare i pesi delle curve. Cambiando i pesi, raramente si ottiene il risultato desiderato e implica calcoli difficili in operazioni come intersezioni. L’unico motivo valido per usare curve razionali è la rappresentazione di curve che altrimenti non possono essere tracciate, come ad esempio cerchi ed ellissi.
Nodi
Ciascuna curva NURBS presenta un elenco di numeri associati chiamati nodi (a volte definiti vettori nodi). I nodi non sono molto facili da capire e impostare. Utilizzando un modellatore 3D, non occorre impostare manualmente i nodi per ciascuna curva creata. Di seguito, vengono spiegate alcune nozioni utili sui nodi.
I nodi come valori parametrici
I nodi rappresentano un elenco di valori parametrici nel dominio di una curva. In Rhino, esistono più nodi di grado meno 1 che punti di controllo. Cioè il numero di nodi è uguale al numero di punti di controllo più il grado della curva meno 1:
|nodi| = |punti di controllo| + grado -1
Di solito, per le curve non periodiche, i nodi del primo grado sono uguali al minimo del dominio e i nodi dell’ultimo grado sono uguali al massimo del dominio.
Ad esempio, i nodi di una curva NURBS di grado 3 aperta con 7 punti di controllo e un dominio compreso fra 0 e 4 potrebbe apparire come <0, 0, 0, 1, 2, 3, 4, 4, 4>.
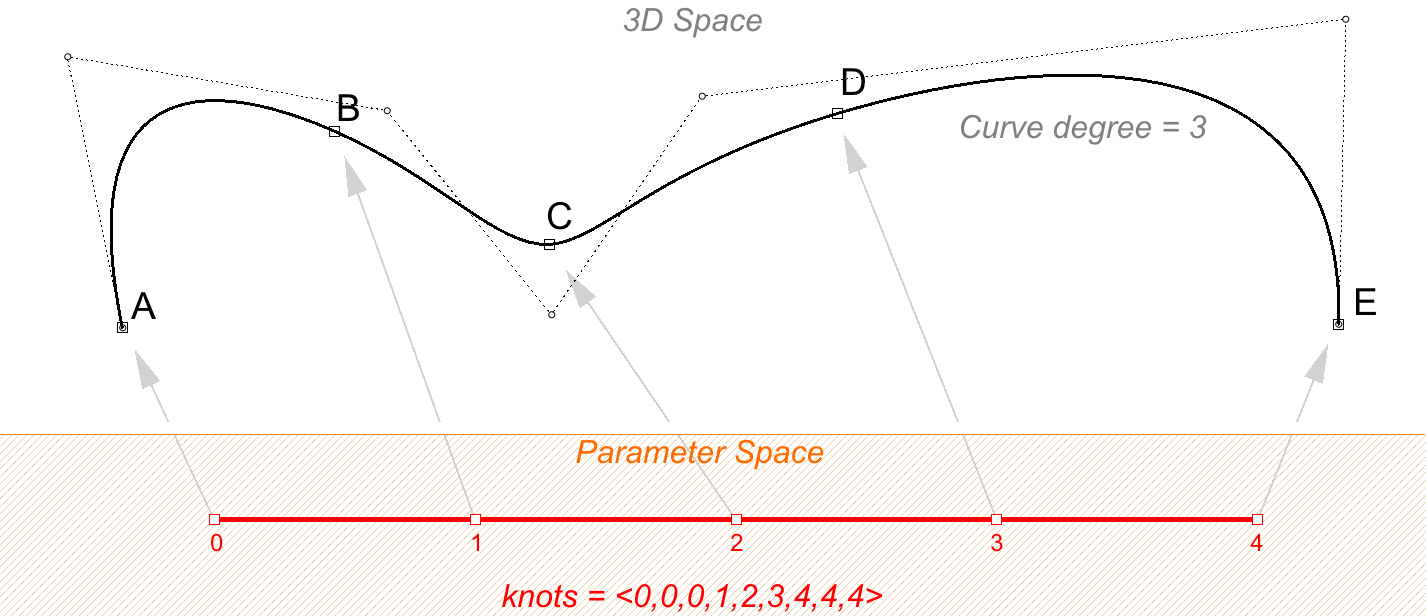
Scalare l’elenco dei nodi non influisce sulla curva 3D. Se cambi il dominio della curva nell’esempio precedente impostando “da 0 a 4” anziché “da 0 a 1”, l’elenco dei nodi viene scalato, ma la curva 3D non cambia.
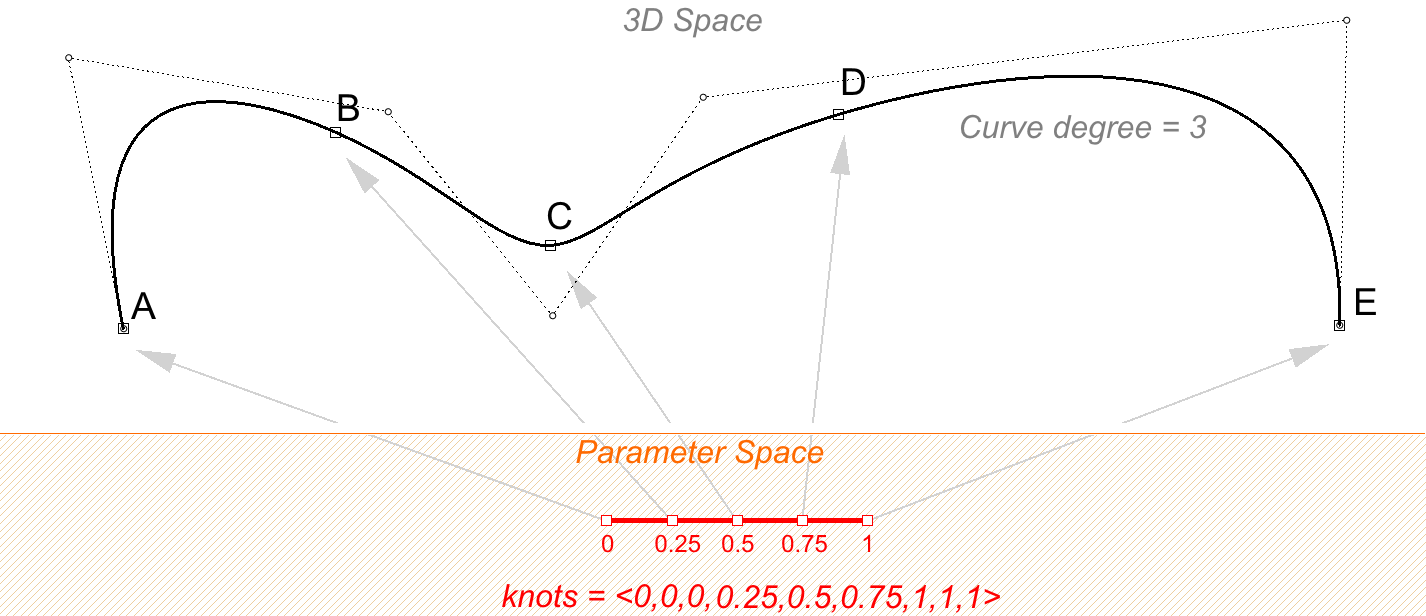
Definiamo nodo semplice un nodo con un valore che appare solo una volta. I nodi interni sono di solito nodi semplici come nei due esempi precedenti.
Molteplicità di nodi
La molteplicità di un nodo è il numero di volte in cui il nodo appare nell’elenco dei nodi. La molteplicità di un nodo non può essere superiore al grado della curva. La molteplicità di nodi viene usata per controllare la continuità nel punto della curva corrispondente.
Nodi a molteplicità piena
Un nodo a molteplicità piena presenta una molteplicità uguale al grado della curva. Un nodo a molteplicità piena presenta il punto di controllo corrispondente e la curva passa attraverso questo punto.
Ad esempio, le curve fisse o aperte presentano nodi a molteplicità piena sugli estremi della curva. Ciò è dovuto al fatto che i punti di controllo finali coincidono con la curva e i punti. I nodi a molteplicità piena consentono un punto di discontinuità nella curva sul punto corrispondente.
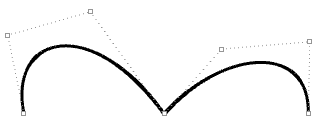
Ad esempio, le due curve seguenti sono entrambe di grado 3 e presentano lo stesso numero di punti di controllo nella stessa posizione. Tuttavia, presentano diversi nodi e anche la loro forma è diversa. La molteplicità piena forza la curva attraverso il punto di controllo associato.
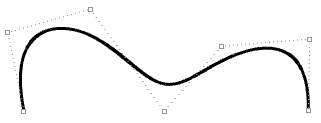
Ecco due curve che hanno lo stesso grado, lo stesso numero e la stessa posizione dei punti di controllo, ma che hanno un vettore di nodi diverso che determina una forma diversa della curva:
| Degree = 3 Numero di punti di controllo = 7 knots = <0,0,0,1,2,3,4,4,4> = 9 knots Dominio (da 0 a 4) |
 |
| Degree = 3 Numero di punti di controllo = 7 knots = <0,0,0,1,1,1,4,4,4> = 9 knots Dominio (da 0 a 4) Nota: un nodo a molteplicità piena al centro crea un punto di discontinuità e la curva viene forzata a passare per il punto di controllo associato. |
 |
Nodi uniformi
Un elenco uniforme di nodi in curve aperte soddisfa la seguente condizione:
I nodi che iniziano con un nodo a molteplicità piena sono seguiti da nodi semplici e terminano con un nodo a molteplicità piena. I valori aumentano a intervalli uguali. Questa è una caratteristica tipica delle curve fisse o aperte. Le curve chiuse periodiche funzionano in modo diverso come vedremo in seguito.
Nodi non uniformi
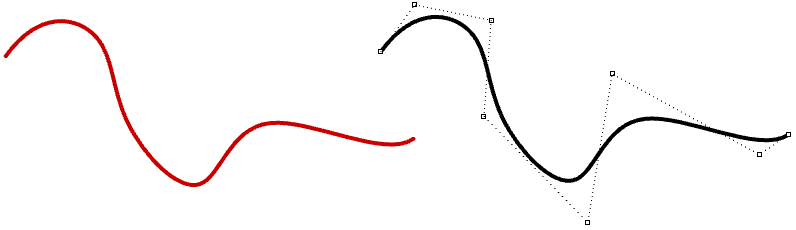
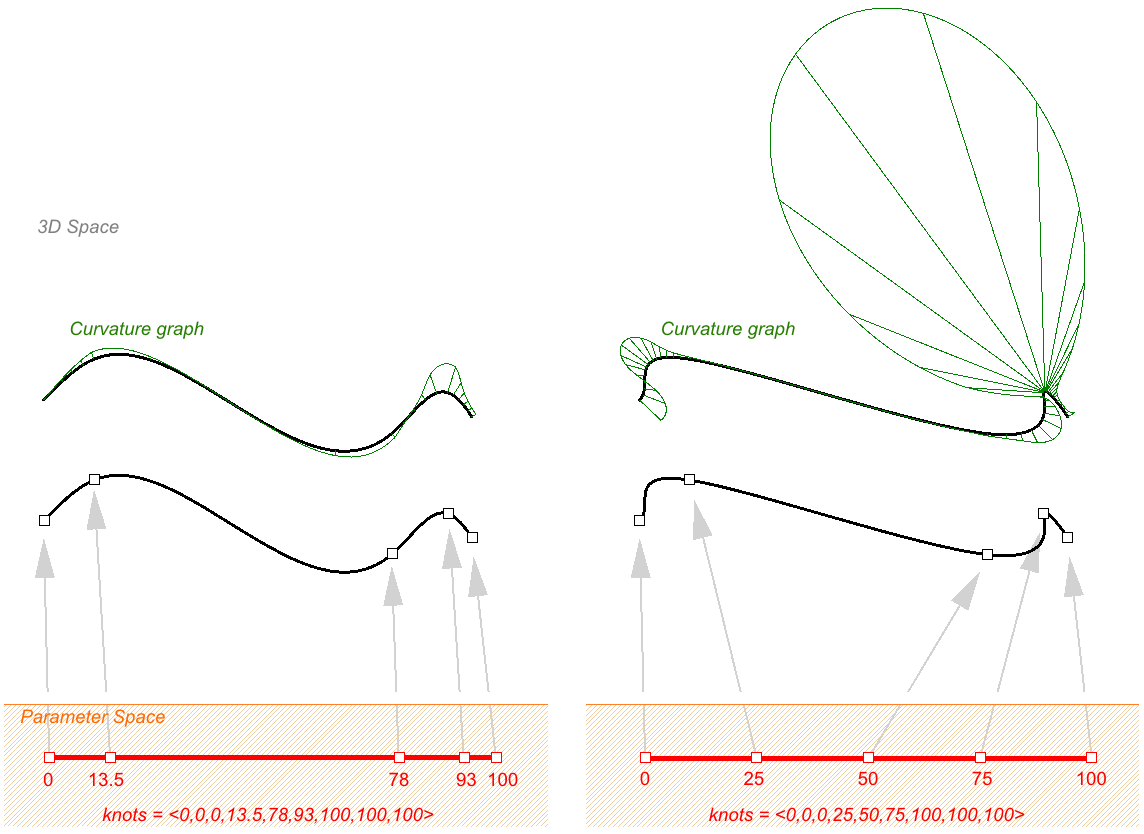
Le curve NURBS vengono usate per ottenere spazi non uniformi fra i nodi. Ciò può aiutare a controllare la curvatura lungo la curva per creare curve più uniformi. Il seguente esempio mostra l’interpolazione attraverso punti usando l’elenco di nodi non uniformi a sinistra e nodi uniformi a destra. In generale, se lo spazio fra nodi di una curva NURBS è proporzionale allo spazio fra i punti di controllo, la curva è più uniforme.
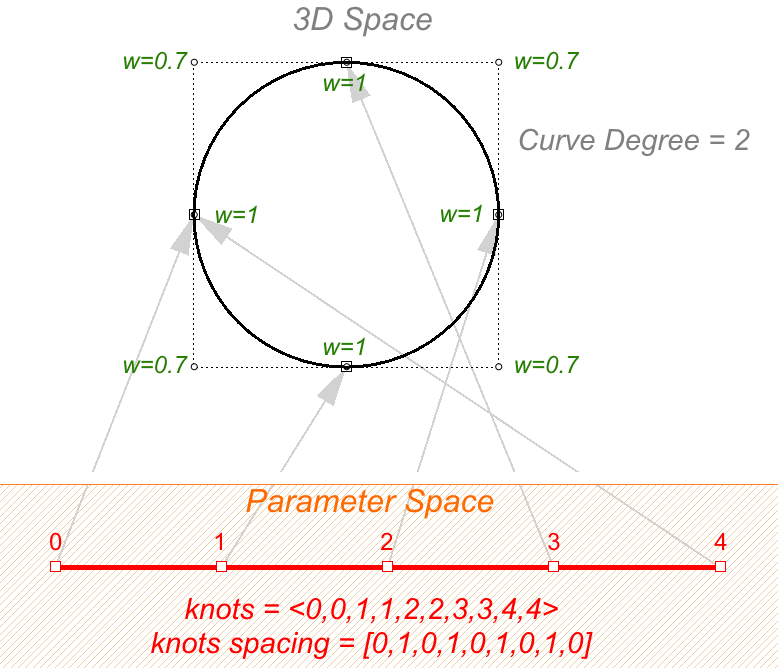
Un esempio di curva non uniforme e razionale è rappresentato da un cerchio NURBS. L’esempio seguente è una curva di grado 2 con 9 punti di controllo e 10 nodi. Il dominio è compreso fra 0 e 4 e lo spazio alternato è compreso fra 0 e 1. knots = <0,0,1,1,2,2,3,3,4,4> — (full multiplicity in the interior knots) spazio fra nodi = [0,1,0,1,0,1,0,1,0] — (non-uniform)
Regola di stima
La regola di stima utilizza una formula matematica che assegna un punto a un numero nel dominio di una curva. La formula prende in considerazione il grado, i punti di controllo e i nodi.
Usando questa formula, le funzioni di curva specializzate usano il parametro di una curva e creano il punto corrispondente su tale curva. Un parametro è un numero sul dominio di una curva. Di solito, i domini aumentano e sono formati da due numeri: il parametro di dominio minimo $$t(0)$$ viene considerato punto iniziale della curva e il parametro massimo $$t(1)$$ viene considerato il punto finale della curva.
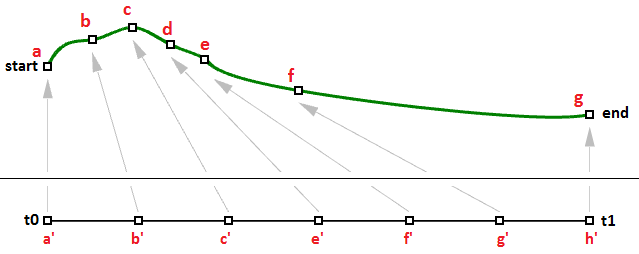
Caratteristiche delle curve NURBS
Per creare una curva NURBS, occorre fornire le informazioni seguenti:
- Dimensione, di solito 3.
- Grado, (a volte usa l’ordine che è uguale al grado+1).
- Punti di controllo (elenco di punti).
- Peso del punto di controllo (elenco di numeri).
- Nodi (elenco di numeri).
Quando viene creata una curva, occorre definire almeno il grado e le posizioni dei punti di controllo. Il resto delle informazioni necessarie per costruire le curve NURBS possono essere ricavate automaticamente. Selezionare il punto di fine, per farlo coincidere con il punto di inizio, crea di solito una curva chiusa periodica. La seguente tabella mostra esempi di curve aperte e chiuse:
| Curva aperta di grado 1. La curva attraversa tutti i punti di controllo. |
 |
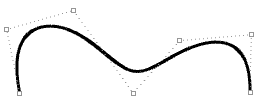
| Curva aperta di grado 3. Entrambi gli estremi della curva coincidono con i punti di controllo. |
 |
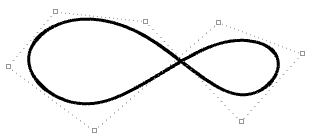
| Curva periodica chiusa di grado 3. Il punto di giunzione della curva non attraversa un punto di controllo. |
 |
| Lo spostamento dei punti di controllo di una curva periodica non influisce sull'uniformità della curva. | 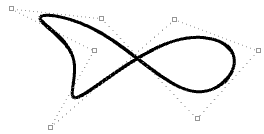 |
| I punti di discontinuità vengono creati quando si forza la curva a passare per alcuni punti di controllo. | 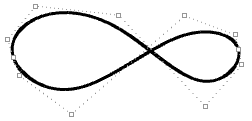 |
| Spostare i punti di controllo di una curva non periodica non garantisce la continuità uniforme di una curva, ma consente un maggiore controllo sul risultato. | 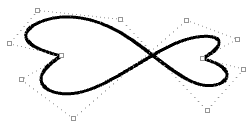 |
Curve fisse e curve NURBS periodiche
I punti di fine di curve fisse chiuse coincidono con i punti di controllo di fine. Le curve periodiche sono curve chiuse uniformi. Il modo migliore per capire le differenze fra i due tipi di curva è confrontarne i punti di controllo e i nodi.
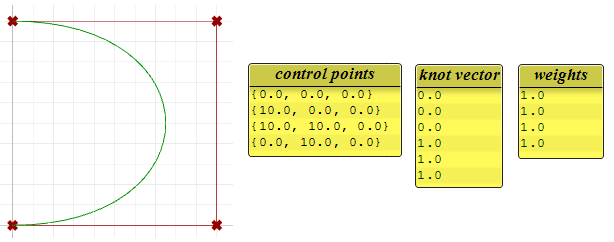
L’esempio seguente mostra una curva NURBS non razionale, fissa e aperta. Questa curva presenta quattro punti di controllo, nodi uniformi a molteplicità piena in corrispondenza dei nodi di inizio e di fine e i pesi di tutti i punti di controllo sono uguali a 1.

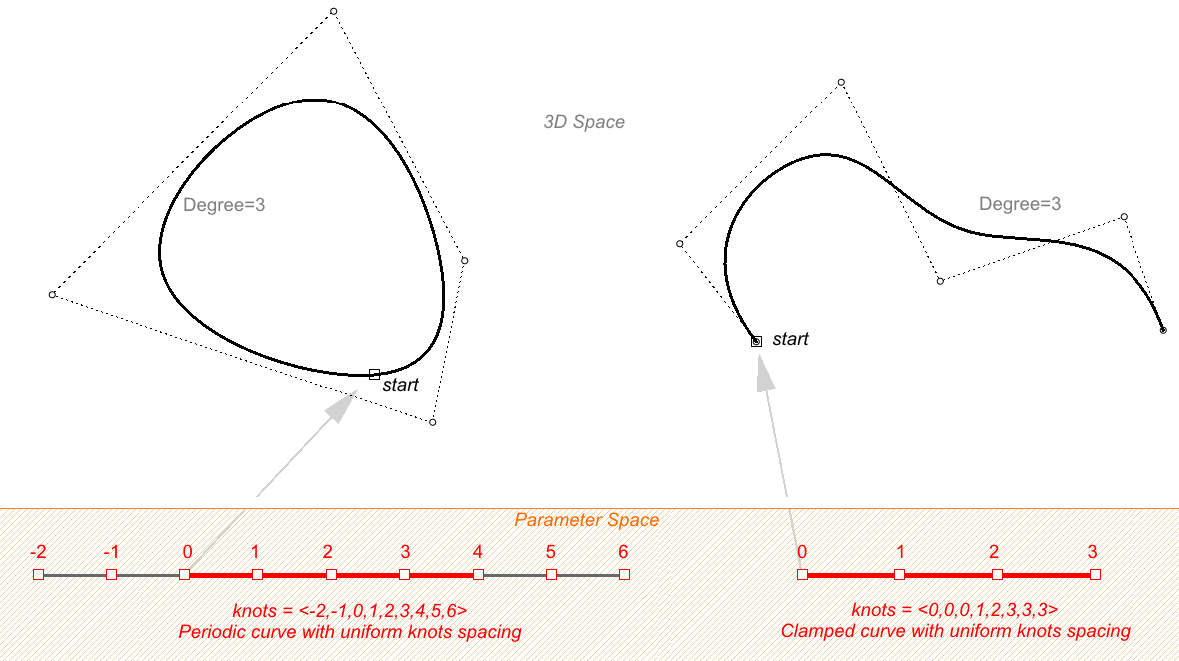
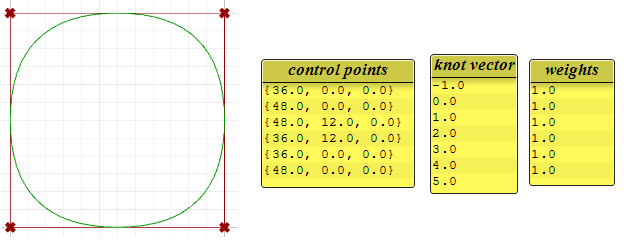
La seguente curva circolare è un esempio di curva NURBS periodica chiusa di grado 3. È anche non razionale poiché tutti i pesi sono uguali. Nota: le curve periodiche richiedono più punti di controllo con alcune sovrapposizioni. Inoltre, i nodi sono nodi semplici.
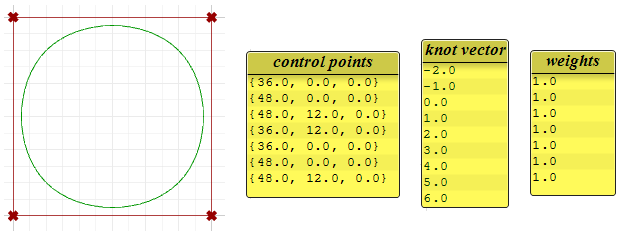
Nota: la curva periodica converte i quattro punti di input in sette punti di controllo (di grado+4) mentre la curva fissa usa solo i quattro punti di controllo. La curva periodica utilizza solo nodi semplici mentre i nodi di inizio e di fine di una curva fissa presentano molteplicità piena, forzando la curva ad attraversare i punti di controllo di inizio e di fine.
Se impostiamo il grado degli esempi precedenti su 2 anziché su 3, i nodi diventano più piccoli e il numero di punti di controllo di curve periodiche cambia.
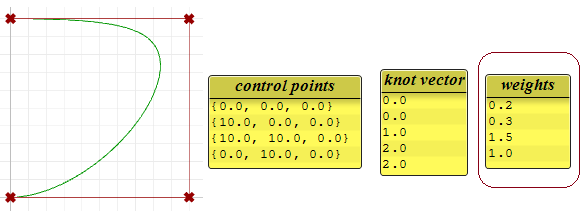
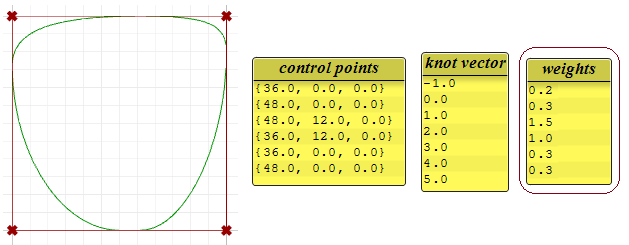
Pesi
I pesi dei punti di controllo in una curva NURBS uniforme sono impostati su 1, ma questo numero può cambiare in curve NURBS razionali. L’esempio seguente mostra l’effetto della variazione dei pesi dei punti di controllo.
Valutazione delle curve NURBS
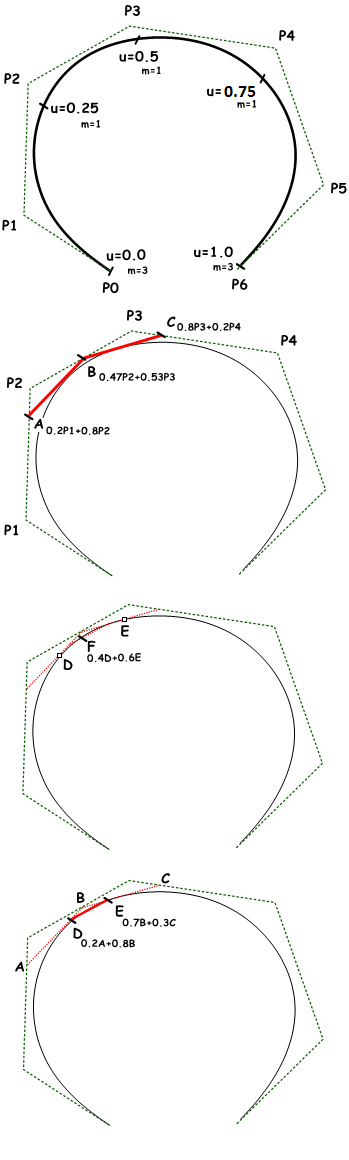
Dal nome del proprio inventore, Carl de Boor, l’algoritmo di De Boorè una generalizzazione dell’algoritmo di Casteljau per le curve di Bézier. Si tratta di un algoritmo numericamente stabile, ampiamente usato per valutare punti sulle curve NURBS in applicazioni 3D. Il seguente esempio si riferisce alla valutazione di un punto su una curva NURBS di grado 3 usando l’algoritmo di De Boor.
Input:
Sette punti di controllo da
$$P0$$ a
$$P6$$
Nodi:
$$u_0 = 0.0$$
$$u_1 = 0.0$$
$$u_2 = 0.0$$
$$u_3= 0.25$$
$$u_4 = 0.5$$
$$u_5 = 0.75$$
$$u_6 = 1.0$$
$$u_7 = 1.0$$
$$u_8 = 1.0$$
Output:
Punto su curva, ovvero in $$u=0.4$$
Soluzione:
1. Calcolo dei coefficienti per la prima iterazione:
$$A_c = ((u – u_1)/(u_{1+3} – u_1) = 0.8$$
$$B_c = (u – u_2)/(u_{2+3} – u_2) = 0.53$$
$$C_c = (u – u_3)/(u_{3+3} – u_3) = 0.2$$
2. Calcolo dei punti usando i dati di coefficiente:
$$A = 0.2P_1 + 0.8P_2$$
$$B = 0.47 P_2 + 0.53 P_3$$
$$C = 0.8 P_3 + 0.2 P_4$$
3. Calcolo dei coefficienti per la seconda iterazione:
$$D_c = (u – u_2) / (u_{2+3-1} – u_2) = 0.8$$
$$E_c = (u – u_3) / (u_{3+3-1} – u_3) = 0.3$$
4. Calcolo dei punti usando i dati di coefficiente:
$$D = 0.2A+ 0.8B$$
$$E = 0.7B + 0.3C$$
5. Calcolo dell’ultimo coefficiente:
$$Fc = (u – u_3)/ (u_{3+3-2} – u_3) = 0.6$$
Trova il punto sulla curva nel parametro $$u=0.4$$:
$$F= 0.4D + 0.6E$$
3.3 Continuità geometrica delle curve
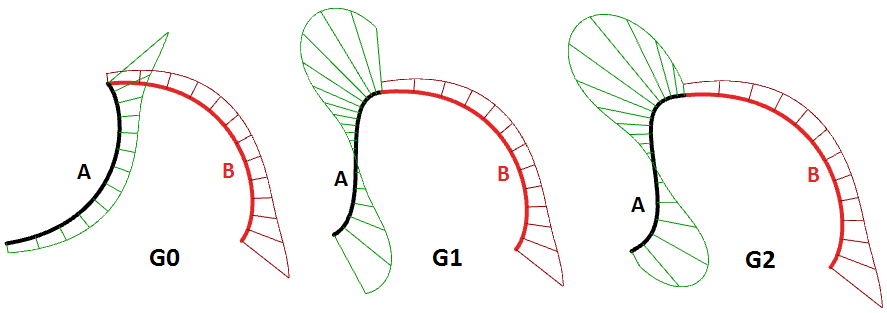
La continuità è un concetto importante nella modellazione 3‑D. La continuità è importante per ottenere uniformità visiva, illuminazione tenue e flusso dell’aria. La seguente tabella mostra varie continuità e le definizioni corrispondenti:
| G0| (posizione continua) | Due segmenti di curva uniti insieme |
| G1| (tangente continua) | La direzione di una tangente nel punto di unione è la stessa per entrambi i segmenti di curva. |
G2| (curvatura continua) | Le curvature così come le tangenti concordano con entrambi i segmenti di curva nel punto finale comune. |
| GN|……. | Le curve concordano con un ordine più alto |
3.4 Curvatura
La curvatura è un concetto ampiamente usato nella modellazione 3‑D di curve e superfici. La curvatura è definita come la variazione di inclinazione di una tangente su una curva, sulla lunghezza di unità di un arco. Per un cerchio o una sfera, la curvatura è il reciproco del raggio ed è costante sull’intero dominio.
In qualsiasi punto di una curva sul piano, la linea che si avvicina di più alla curva che attraversa questo punto è la linea tangente. Possiamo anche trovare il cerchio che si avvicina di più, che attraversa questo punto e che è tangente alla curva. Il reciproco del raggio di questo cerchio è la curvatura della curva in questo punto.
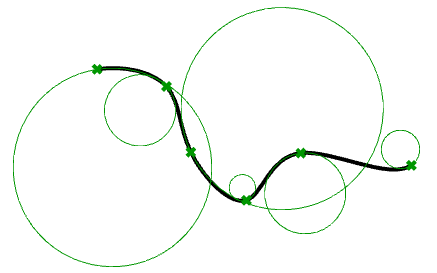
Il cerchio che si avvicina di più può trovarsi a destra o a sinistra. In questo senso, possiamo per esempio assegnare un segno positivo alla curvatura se il cerchio si trova a sinistra della curva e un segno negativo se si trova a destra della curva. Questo concetto viene denominato curvatura con segno. I valori di curvatura di curve unite indicano la continuità fra le curve.
3.5 Superfici parametriche
Parametri di superficie
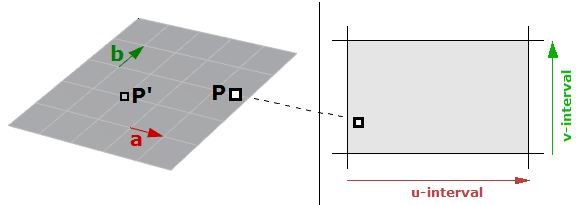
Una superficie parametrica è una funzione di due parametri indipendenti (indicati normalmente come $$u$$, $$v$$) su domini bidimensionali. Prendiamo come esempio un piano. Se abbiamo un punto $$P$$ sul piano e due vettori non paralleli sul piano, $$\vec a$$ e $$\vec b$$ allora possiamo definire un’equazione del piano parametrica in termini di due parametri $$u$$ e $$v$$ come segue:
$$P = P’ + u * \mathbf{\vec a} + v * \mathbf{\vec b}$$Dove:
$$P’$$: è un punto noto sul piano.
$$\mathbf{\vec a}$$: è il primo vettore sul piano.
$$\mathbf{\vec b}$$: è il primo vettore sul piano.
$$u$$: è il primo parametro.
$$v$$: è il primo parametro.
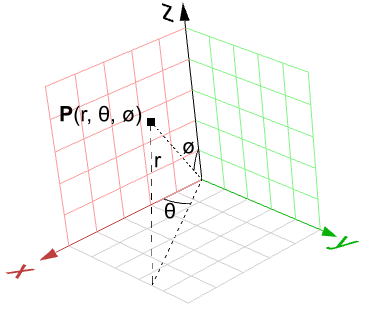
Un altro esempio è la sfera. L’equazione cartesiana di una sfera centrata nell’origine con il raggio $$R$$ è
$$x^2 + y^2 + z^2 = R^2$$Ciò vuol dire che per ciascun punto esistono tre variabili ( $$x$$, $$y$$, $$z$$), questo scenario non è utile per una rappresentazione parametrica che richiede due variabili. Tuttavia, nel sistema di coordinate sferiche, ciascun punto viene trovato usando i tre valori:
$$r$$: distanza radiale tra il punto e l’origine.
$$θ$$: l’angolo dall’asse x sul piano xy.
$$ø$$: l’angolo tra l’asse z e il punto.
È possibile ottenere una conversione di punti da coordinate sferiche a coordinate cartesiane come segue:
$$x = r * sin(ø) * cos(θ)$$
$$y = r * sin(ø) * sin(θ)$$
$$z = r * cos (ø)$$
Dove:
$$r$$ è la distanza dall’origine
$$≥ 0$$
$$θ$$ è in esecuzione da
$$0$$ a
$$2π$$
$$ø$$ è in esecuzione da
$$0$$ a
$$π$$
Poiché $$r$$ è costante in una superficie sferica, abbiamo lasciato solo due variabili, quindi possiamo usare l’esempio precedente per creare una rappresentazione parametrica di una superficie sferica:
$$u = θ$$
$$v = ø$$
Quindi abbiamo:
$$x = r * sin(v) * cos(u)$$
$$y = r * sin(v) * sin(u)$$
$$z = r * cos(v)$$
Where ( $$u$$, $$v$$) è all’interno del dominio ( $$2 π$$, $$π$$)
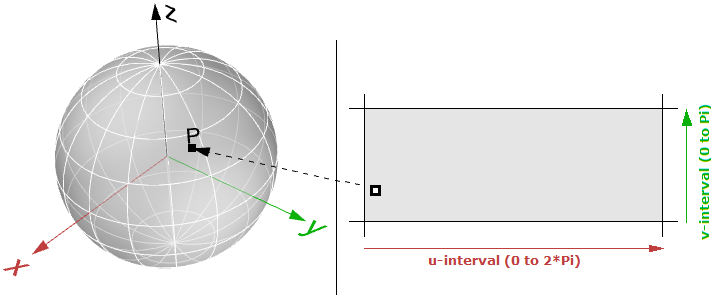
La superficie parametrica segue la forma generale:
$$x = x(u,v)$$
$$y = y(u,v)$$
$$z = z(u,v)$$
Dove:
$$u$$ e $$v$$ sono due parametri nel dominio o regione della superficie.
Dominio di superficie
Un dominio di superficie è definito come intervallo di ( $$u,v$$) parametri valutati in un punto 3D sulla superficie. Il dominio in ciascuna dimensione ( $$u$$ o $$v$$) è di solito descritto come due numeri reali ( $$u_{min}$$ a $$u_{max}$$) e ( $$v_{min}$$ a $$v_{max}$$)
Cambiare un dominio di superficie significa riparametrizzare la superficie. Un dominio crescente indica che il valore minimo del dominio punta verso il punto minimo della superficie. Di solito i domini sono crescenti, ma non sempre.
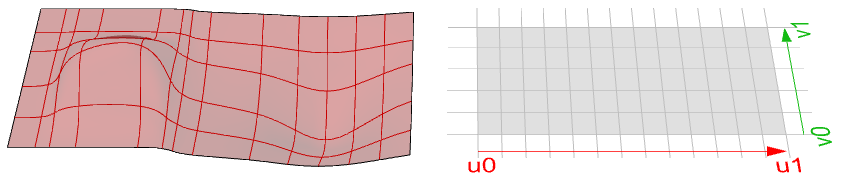
Valutazione di una superficie
Valutare una superficie in un parametro nel dominio di una superficie crea un punto che si trova sulla superficie. Occorre tenere in considerazione che il centro del dominio ( $$u_{mid}$$, $$v_{mid}$$) potrebbe non necessariamente essere considerato il punto centrale della superficie 3D. Inoltre, considerare i valori $$u-$$ e $$v-$$ che si trovano al di fuori del dominio della superficie non fornirà un risultato utile.
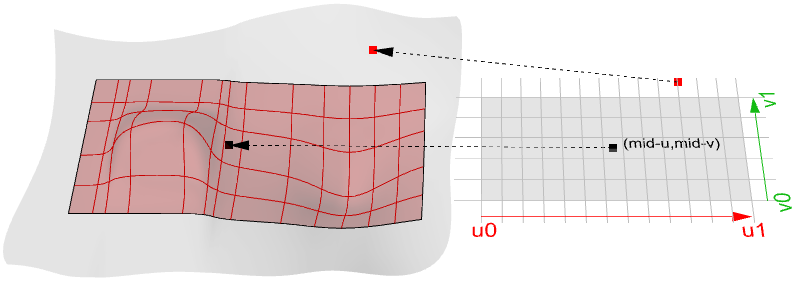
Piano tangente di una superficie
Il piano tangente di una superficie in un determinato punto è rappresentato dal piano che tocca la superficie in quel punto. La direzione z del piano tangente rappresenta la direzione alla normale della superficie in quel punto.
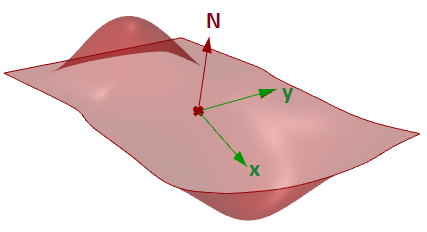
3.6 Continuità geometrica delle superfici
Numerosi modelli non possono essere costruiti da patch di superfici. La continuità fra patch di superfici unite è importante per ottenere uniformità visiva, riflessione della luce e flusso dell’aria. La seguente tabella mostra varie continuità e le definizioni corrispondenti:
| G0| (Posizione continua) | Due superfici unite. |
| G1| (Tangenti continue) | Le tangenti corrispondenti delle due superfici lungo il bordo di unione sono parallele sia nella direzione u che v. |
| G2| (Curvatura continua) | Le curvature così come le tangenti concordano con entrambe le superfici sul bordo comune. |
| GN|……. Le superfici concordano con un ordine più alto. |
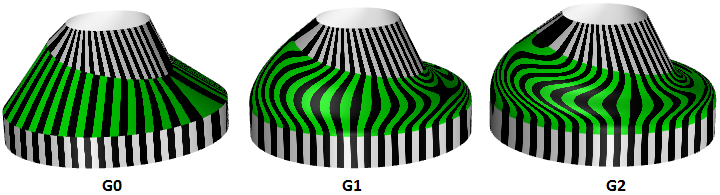
3.7 Curvatura di una superficie
Per le superfici, la curvatura della normale è una generalizzazione della curvatura sulle superfici. Dato un punto sulla superficie ed una direzione situata sul piano tangente della superficie in quel punto, la curvatura della sezione della normale viene calcolata intersecando la superficie con il piano suddiviso dal punto, la normale alla superficie in quel punto e la direzione. La curvatura della sezione della normale è la curvatura con segno di questa curva nel punto preso in considerazione.
Se guardiamo in tutte le direzioni sul piano tangente alla superficie nel punto analizzato e calcoliamo la curvatura della sezione della normale in tutte le direzioni, otterremo un valore massimo e un valore minimo.
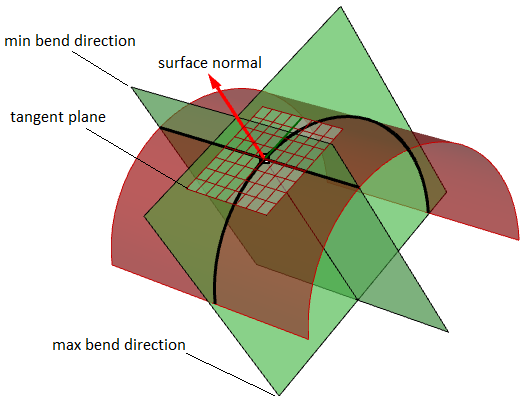
Curvature principali
Le curvature principali di una superficie in un punto rappresentano il minimo ed il massimo delle curvature normali in quel punto. Misurano la quantità di piegatura massima e minima della superficie in quel punto. Le curvature principali si usano per calcolare la curvatura Gaussiana e le curvature medie di una superficie.
Ad esempio, in una superficie cilindrica, non esiste una piegatura nella direzione lineare (curvatura uguale a zero) mentre la piegatura massima si verifica durante l’intersezione con un piano parallelo alle facce di fine (curvatura uguale a 1/raggio). Quelle con due estremi creano le curvature principali di tale superficie.
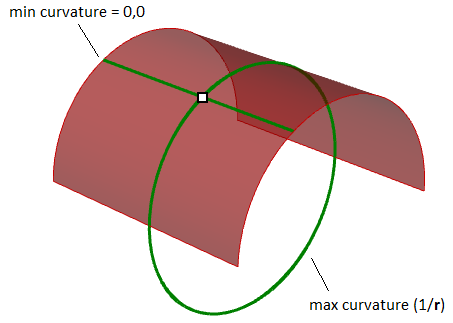
Curvatura gaussiana
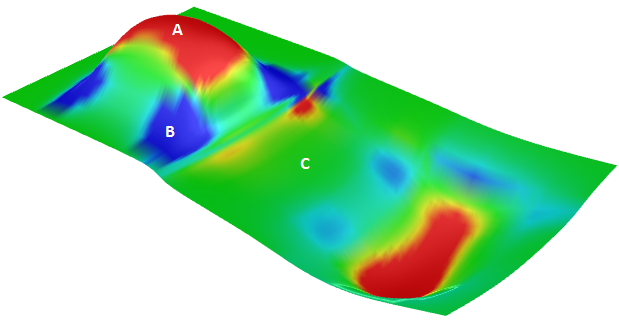
La curvatura gaussiana di una superficie in un punto è il prodotto delle curvature principali in quel punto. Il piano tangente di qualsiasi punto con curvatura gaussiana positiva tocca la superficie in un solo punto, mentre il piano tangente di qualsiasi punto con curvatura gaussiana negativa taglia la superficie.
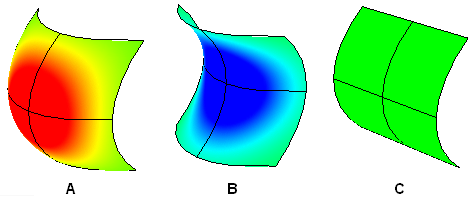
A: Curvatura positiva quando la superficie è concava.
B: Curvatura negativa quando la superficie è convessa.
C: Curvatura pari a zero quando la superficie è piana almeno in una direzione (piano, cilindro).
Curvatura media
La curvatura media di una superficie in un punto è la metà della somma delle curvature principali in quel punto. Qualsiasi punto con curvatura media pari a zero presenta una curvatura gaussiana negativa o pari a zero.
Le superfici con curvatura media in qualsiasi punto pari a zero vengono denominate superfici minime. I processi fisici che possono essere modellati con superfici minime comprendono la formazione di pellicole di sapone che si estendono su oggetti fissi, come per esempio un cappio a filo metallico. Una pellicola di sapone non viene deformata dalla pressione dell’aria (che è uguale da entrambi i lati) ed è libera di minimizzare la propria area. Una bolla di sapone, invece, racchiude una quantità fissa di aria ed ha pressioni diverse al suo interno ed al suo esterno. La curvatura media è utile per trovare zone di variazioni brusche sulla superficie della curvatura.
Le superfici con curvatura media costante in qualsiasi punto vengono definite superfici CMC (a curvatura media costante). Le superfici a curvatura media costante includono la formazione di bolle di sapone, sia libere che attaccate agli oggetti. Una bolla di sapone, diversamente da una semplice pellicola, racchiude un volume ed esiste in uno stato di equilibrio, dove la pressione leggermente maggiore all’interno della bolla viene equilibrata dalle forze della superficie minima della bolla stessa.
3.8 Superfici NURBS tagliate
È possibile paragonare le superfici NURBS a una griglia con curve NURBS che vanno in due direzioni. La forma di una superficie NURBS viene definita da un numero di punti di controllo e dal grado della superficie in ciascuna delle due direzioni (direzioni u e v). Le superfici NURBS sono efficienti per archiviare e rappresentare superfici free-form con un alto livello di precisione. Le equazioni matematiche e le informazioni sulle superfici NURBS vanno oltre le finalità di questo testo. Ci soffermeremo quindi solo sulle caratteristiche più utili ai progettisti.
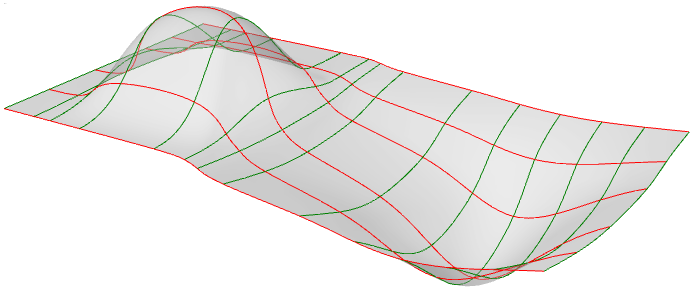
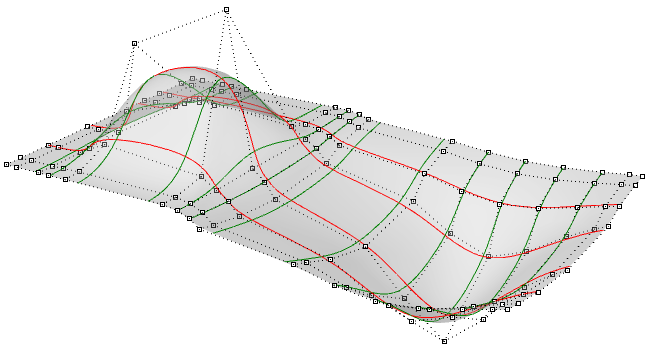
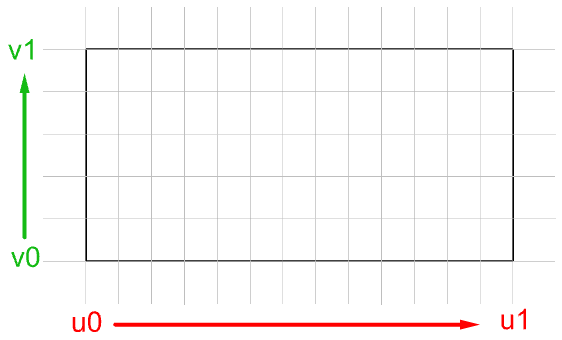
Nella nella maggior parte dei casi, valutare i parametri a intervalli uguali nel rettangolo parametrico 2D non si traduce in intervalli uguali in uno spazio 3D.
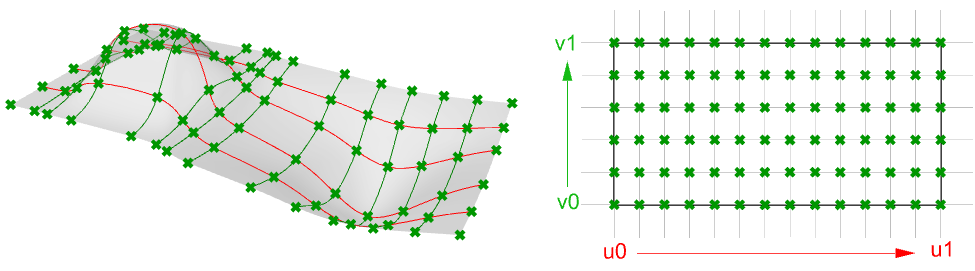
Caratteristiche delle superfici NURBS
Le caratteristiche delle superfici NURBS sono molto simili a quelle delle curve NURBS e si distinguono solo per la presenza di un parametro aggiuntivo. Le superfici NURBS implicano i seguenti dettagli:
- Dimensione, di solito 3.
- Il grado nelle direzioni U e V. (a volte si usa l’ordine di grado + 1).
- Punti di controllo (punti).
- Pesi dei punti di controllo (numeri).
- Nodi (numeri).
Come nelle curve NURBS, probabilmente non occorre sapere come creare una superficie NURBS, poiché i modellatori 3D forniscono di solito strumenti utili per farlo. È comunque possibile ricostruire superfici e curve per un nuovo grado e un nuovo numero di punti di controllo. Le superfici possono essere aperte, chiuse o periodiche. Ecco alcuni esempi di superfici:
| Superficie di grado 1 in entrambe le direzioni u e v. Tutti i punti di controllo giacciono sulla superficie. | 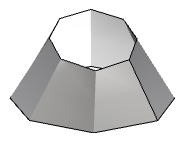 |
| Superficie aperta di grado 3 nella direzione u e di grado 1 nella direzione v. I vertici della superficie coincidono con i punti di controllo dei vertici. | 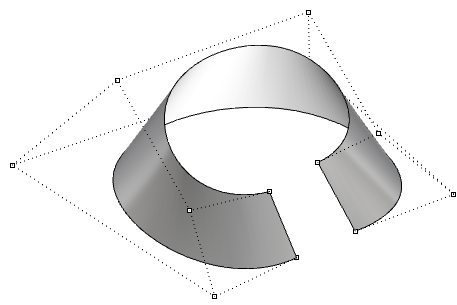 |
| Superficie non periodica chiusa di grado 3 nella direzione u e di grado 1 nella direzione v. Alcuni punti di controllo coincidono con la giunzione della superficie. | 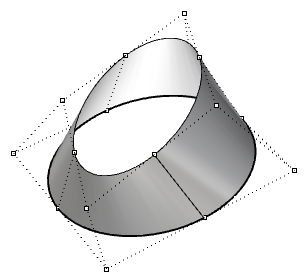 |
| Spostare i punti di controllo di una superficie non periodica chiusa crea un punto di discontinuità e quindi la superficie non appare uniforme. | 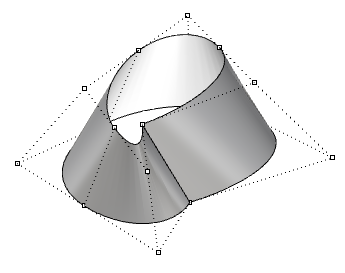 |
| Superficie periodica di grado 3 nella direzione u e di grado 1 nella direzione v. I punti di controllo non coincidono con la giunzione della superficie. | 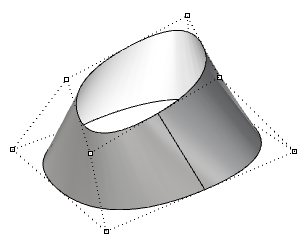 |
| Spostare i punti di controllo di una superficie periodica non influisce sull'uniformità della superficie o sulla creazione di punti di discontinuità. | 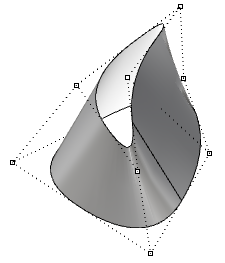 |
Singolarità delle superfici NURBS
Ad esempio, se in un bordo lineare di un piano semplice trascini due punti di controllo finali di un angolo, questi si sovrappongono (collassano) al centro in modo da ottenere un bordo singolo. Nota: le isocurve di superficie convergono nel punto singolo.
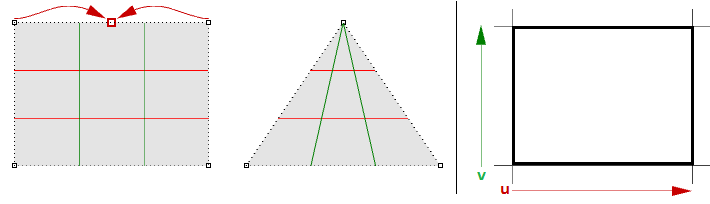
La forma triangolare precedente può essere creata senza singolarità. È possibile tagliare una superficie con una polilinea del triangolo. Quando esamini la struttura NURBS sottostante, questa rimane di forma rettangolare.
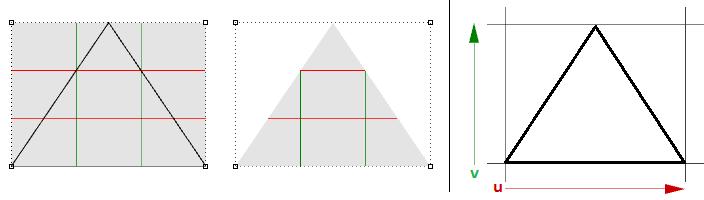
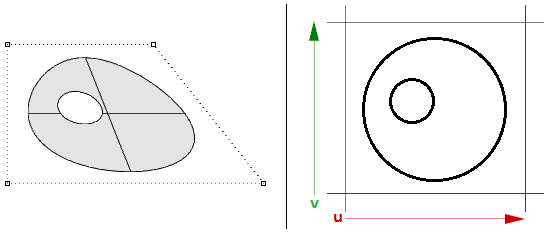
Altri comuni esempi di superfici difficili da creare senza singolarità sono rappresentati dal cono o dalla sfera. La parte superiore di un cono e i bordi inferiori di una sfera vengono collassati in un punto. Indipendentemente dal fatto che esista la singolarità, il rettangolo parametrico mantiene più o meno la regione rettangolare.
Superfici NURBS tagliate
Le superfici NURBS possono essere tagliate o non tagliate. Le superfici tagliate usano la superficie NURBS sottostante e curve chiuse per tagliare parte della superficie. Ciascuna superficie presenta una curva chiusa che definisce il bordo più esterno (ciclo esterno) e può presentare curve interne chiuse non intersecanti per definire fori (cicli interni). Una superficie con un ciclo più esterno uguale a quello della superficie NURBS sottostante e che non presenta fori viene definita superficie non tagliata.
3.9 Polisuperfici
Una polisuperficie è formata da due o più superfici NURBS (possibilmente tagliate) unite tra di loro. Ciascuna superficie presenta la propria struttura, parametrizzazione e direzioni di isocurve che non devono coincidere. Le polisuperfici vengono rappresentate usando la rappresentazione del contorno (BRep). La struttura BRep descrive superfici, bordi e vertici con dati di taglio e connettività fra le varie parti. La superficie tagliata è rappresentata anche dalla struttura dati BRep.

BRep è una struttura dati che descrive ciascuna faccia in termini di superficie sottostante, bordi 3D circostanti, vertici, tagli 2D dello spazio parametrico e rapporto tra le facce vicine. Gli oggetti BRep vengono chiamati anche solidi quando sono chiusi (perfettamente chiuse).
Un esempio di polisuperficie è un parallelepipedo semplice composto da sei superfici non tagliate unite insieme.
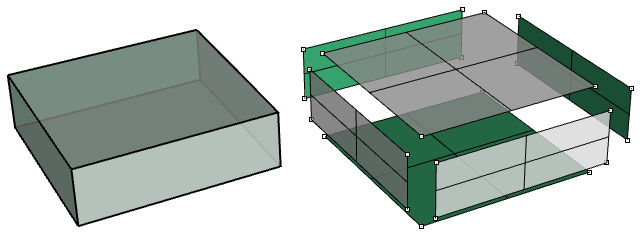
Lo stesso parallelepipedo può essere creato usando le superfici tagliate, così come quello superiore mostrato nell’esempio seguente.
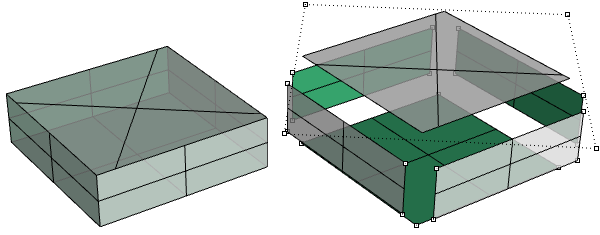
La faccia superiore e la faccia inferiore del cilindro nell’esempio seguente sono tagliate dalle superfici planari.
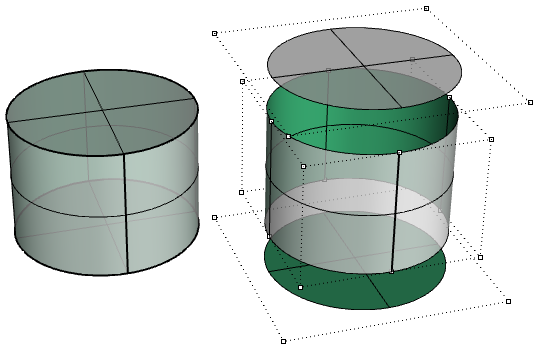 La figura (72) mostra i punti di controllo delle superfici sottostanti.
La figura (72) mostra i punti di controllo delle superfici sottostanti.
Abbiamo visto che la modifica di curve NURBS e di superfici non tagliate è un processo intuitivo che può essere eseguito in modo interattivo spostando i punti di controllo. Tuttavia, la modifica di superfici e polisuperfici tagliate può rappresentare una vera e propria impresa. La sfida principale è mantenere uniti i bordi uniti di varie facce entro la tolleranza desiderata. Le facce vicine che condividono facce comuni possono essere tagliate e di solito non devono coincidere con la struttura NURBS; quindi, modificare l’oggetto in modo da deformare il bordo comune, potrebbe creare un intervallo.
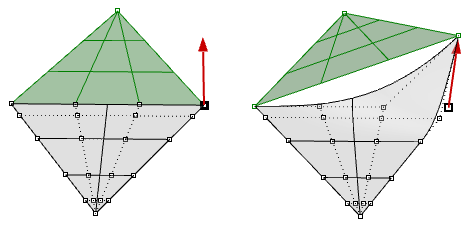
Un’altra sfida è rappresentata da un controllo minore sul risultato, specialmente durante la modifica della geometria tagliata.
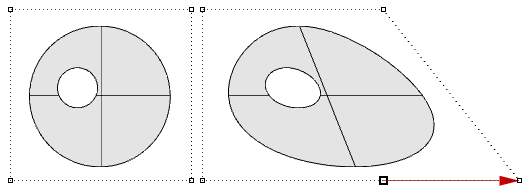
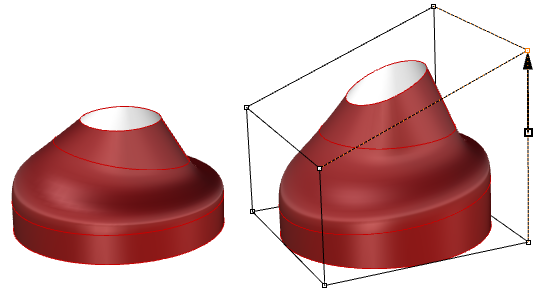
Le superfici tagliate vengono descritte nello spazio parametrico usando la superficie sottostante non tagliata combinata con le curve tagliate 2D che corrispondono ai bordi 3D nella superficie 3D.
3.10 Tutorial
I seguenti tutorial utilizzano i concetti appresi in questo capitolo. Utilizzano Rhinoceros 5 e Grasshopper 0.9.
3.10.1 Continuità tra le curve
Esaminare la continuità fra due curve di input. La continuità implica che le curve si incontrino in corrispondenza della fine della prima curva e l’inizio della seconda curva.
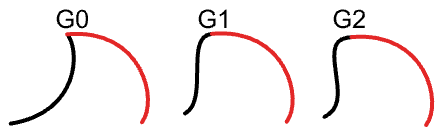
Input:
Due curve di input.
Parametri:
Calcolare quanto segue per poter stabilire la continuità fra due curve:
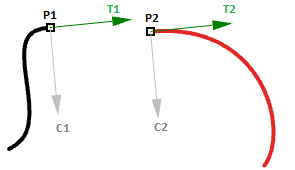
- Il punto di fine della prima curva ( $$P1$$)
- Il punto di inizio della seconda curva ( $$P2$$)
- La tangente in corrispondenza della fine della prima curva e all’inizio della seconda curva ( $$T1$$ e $$T2$$).
- La curvatura in corrispondenza della fine della prima curva e all’inizio della seconda curva ( $$C1$$ e $$C2$$).
Soluzione:
1. Riparametrizzare le Curve in input. Eseguiamo questa operazione in modo da sapere che l’inizio della curva coincide con
$$t=0$$ e la fine con
$$t=1$$.
2. Estrarre i punti di inizio e di fine di due curve e controllare se coincidono. Se è così, le due curve presentano almeno una continuità
$$G0$$.
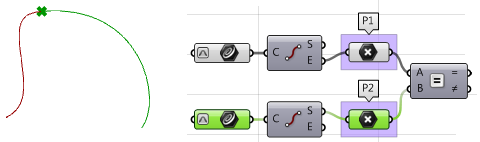
3. Calcolare le tangenti.
4. Confrontare le tangenti usando il prodotto scalare. Assicurarsi di unificare i vettori. Se le curve sono parallele, la continuità sarà almeno
$$G1$$.
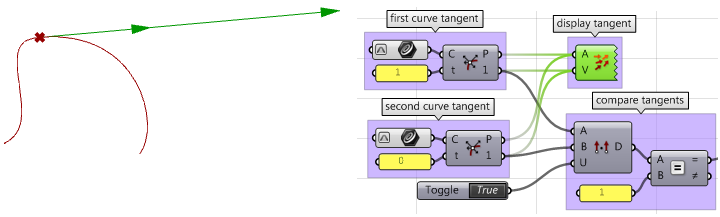
5. Calcolare i vettori di curvatura.
6. Confrontare i vettori di curvatura e, se concordano, le due curve presentano continuità
$$G2$$.
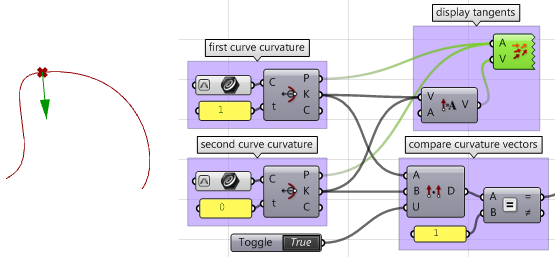
7. Creare una logica che filtra i tre risultati (G1, G2 e G3) e selezionare la continuità più alta.
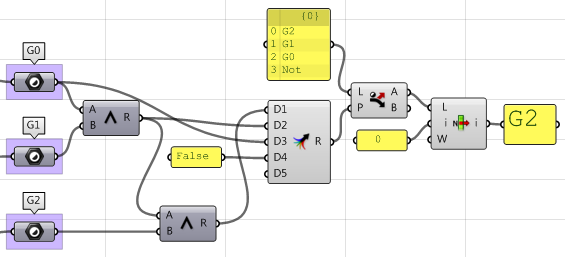
Usare il componente VBScript di Grasshopper:
Private Sub RunScript(ByVal c1 As Curve, ByVal c2 As Curve, ByRef A As Object)
'declare variables
Dim continuity As New String("")
Dim t1, t2 As Double
Dim v_c1, v_c2, c_c1, c_c2 As Vector3d
'extract start and end points
Dim end_c1 = c1.PointAtEnd
Dim start_c2 = c2.PointAtStart
'check G0 continuity
If end_c1.DistanceTo(start_c2) = 0 Then
continuity = "G0"
End If
'check G1 continuity
If continuity = "G0" Then
'calculate tangents
v_c1 = c1.TangentAtEnd
v_c2 = c2.TangentAtStart
'unitize tangent vectors
v_c1.Unitize
v_c2.Unitize
'compare tangents
If v_c1 * v_c2 = 1.0 Then
continuity = "G1"
End If
End If
'check G2 continuity
If continuity = "G1" Then
'extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max
t2 = c2.Domain.Min
'calculate curvature
c_c1 = c1.CurvatureAt(t1)
c_c2 = c2.CurvatureAt(t2)
'unitize curvature vectors
c_c1.Unitize
c_c2.Unitize
'compare vectors
If c_c1 * c_c2 = 1.0 Then
continuity = "G2"
End If
End If
'Assign output
A = continuity
End Sub
Usare il componente Python per Grasshopper:
#decclare variables
continuity = ""
#extract start and end points
end_c1 = c1.PointAtEnd
start_c2 = c2.PointAtStart
#check G0 continuity
if end_c1.DistanceTo(start_c2) == 0:
continuity = "G0"
#check G1 continuity
if continuity == "G0":
#calculate tangents
v_c1 = c1.TangentAtEnd
v_c2 = c2.TangentAtStart
#unitize tangent vectors
v_c1.Unitize()
v_c2.Unitize()
#compare tangents
dot = v_c1 * v_c2
if dot == 1.0:
continuity = "G1"
else:
print("Failed G1")
print(dot)
#check G2 continuity
if continuity == "G1":
#extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max
t2 = c2.Domain.Min
#calculate curvature
c_c1 = c1.CurvatureAt(t1)
c_c2 = c2.CurvatureAt(t2)
#unitize curvature vectors
c_c1.Unitize()
c_c2.Unitize()
#compare vectors
dot = c_c1 * c_c2
if dot == 1.0:
continuity = "G2"
else:
print("Failed G2")
print(dot)
#assign output
A = continuity
Usare il componente C# per Grasshopper:
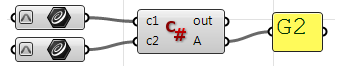
Private Sub RunScript(ByVal c1 As Curve, ByVal c2 As Curve, ByRef A As Object)
//decalre variables
string continuity = ("");
double t1, t2;
Vector3d v_c1, v_c2, c_c1, c_c2;
//extract start and end points
Point3d end_c1 = c1.PointAtEnd;
Point3d start_c2 = c2.PointAtStart;
//check G0 continuity
if( end_c1.DistanceTo(start_c2) == 0){
continuity = "G0";
}
//check G1 continuity
if( continuity == "G0")
{
//calculate tangents
v_c1 = c1.TangentAtEnd;
v_c2 = c2.TangentAtStart;
//unitize tangent vectors
v_c1.Unitize();
v_c2.Unitize();
//compare tangents
if( v_c1 * v_c2 == 1.0 ){
continuity = "G1";
}
}
//check G2 continuity
if( continuity == "G1" )
{
//extract the parameter at start and end of the curves domain
t1 = c1.Domain.Max;
t2 = c2.Domain.Min;
//calculate curvature
c_c1 = c1.CurvatureAt(t1);
c_c2 = c2.CurvatureAt(t2);
//unitize curvature vectors
c_c1.Unitize();
c_c2.Unitize();
//compare vectors
if( c_c1 * c_c2 == 1.0 ){
continuity = "G2";
}
}
//assign output
A = continuity;
End Sub
3.10.2 Surfaces with singularity
Estrarre i punti singolari in una sfera e un cono.
Input:
Una sfera e un cono.
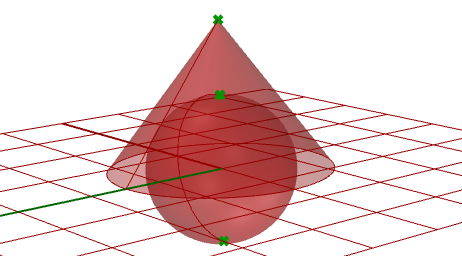
Parametri:
La singolarità può essere rilevata attraverso i tagli dell’analisi dello spazio parametrico 2D che presentano bordi non validi o corrispondenti a lunghezza zero. Tali tagli devono essere singolari.
Soluzione:
- La traversa attraverso tutti i tagli nell’input.
- Controllare se i tagli presentano un bordo non valido e contrassegnarlo come taglio singolare.
- Estrarre posizioni di punti nello spazio 3D.
Usare il componente VB per Grasshopper:
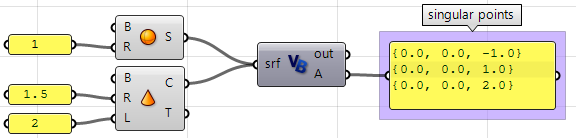
Private Sub RunScript(ByVal srf As Brep, ByRef A As Object)
'Decalre a new list of points
Dim singular_points As New List( Of Point3d)
'Examine all trims in the input
For Each trim As BrepTrim In srf.Trims
'Null edge of a trim indicates a singularity
If trim.Edge Is Nothing Then
'Find the 2D parameter space point of the start or end of the trim
Dim pt2d = New Point2d(trim.PointAtStart)
'Evaluate trim end point on the object surface
Dim pt3d = trim.Face.PointAt(pt2d.x, pt2d.y)
'Add 3D point to the list of singular points
singular_points.Add(pt3d)
End If
Next
'Asign output
A = singular_points
End Sub
Usare il componente Python per Grasshopper:
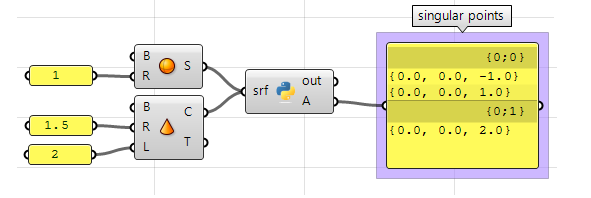
#Decalre a new list of points
singular_points = []
#Examine all trims in the input brep
for trim in srf.Trims:
#Null edge of a trim indicates a singularity
if trim.Edge == None:
#Find the 2D parameter space point at trim start or end
pt2d = trim.PointAtStart
#Evaluate trim end point on the object surface
pt3d = trim.Face.PointAt(pt2d.X, pt2d.Y)
#Add 3D point to the list of singular points
singular_points.append(pt3d)
#Asign output
A = singular_points
Usare il componente C# per Grasshopper:
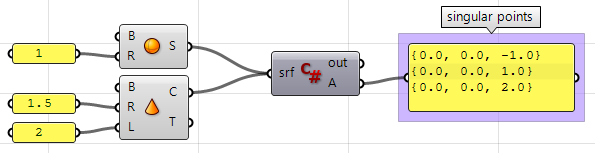
private void RunScript(Brep srf, ref object A)
{
//Decalre a new list of points
List < Point3d > singular_points = new List<Point3d>();
//Examine all trims in the input
foreach( BrepTrim trim in srf.Trims)
{
//Null edge of a trim indicates a singularity
if( trim.Edge == null)
{
//Find the 2D parameter space point of the start or end of the trim
Point2d pt2d = new Point2d(trim.PointAtStart);
//Evaluate trim end point on the object surface
Point3d pt3d = trim.Face.PointAt(pt2d.X, pt2d.Y);
//Add 3D point to the list of singular points
singular_points.Add(pt3d);
}
}
//Asign output
A = singular_points
}
Download dei file di esempio
Download del file math-samplesandtutorials.zip contenente tutti gli esempi di Grasshopper e i file del codice menzionati in questa guida.
Passi successivi
Per ulteriori informazioni, consulta la guida Riferimenti per conoscere la struttura dettagliata delle curve e delle superfici NURBS.

