Un vettore indica una quantità, come la velocità o la forza, con direzione e lunghezza. Nei sistemi di coordinate 3D, i vettori sono rappresentati da un gruppo ordinato di tre numeri reali del tipo:
$$\mathbf{\vec v} = <a_1, a_2, a_3>$$1.1 Rappresentazione vettoriale
In questo documento, le lettere minuscole in grassetto con la freccia in alto indicano i vettori. I componenti vettoriali vengono anche indicati fra parentesi angolari. Le lettere maiuscole indicano i punti. Le coordinate di punti vengono sempre indicate fra parentesi.
Utilizzando un sistema di coordinate e un qualsiasi insieme di punti di ancoraggio, possiamo rappresentare e visualizzare i vettori usando una rappresentazione con segmenti di linee, dove una freccia mostra la direzione del vettore. Una freccia mostra la direzione del vettore.
Ad esempio, se abbiamo un vettore con una direzione parallela all’asse X di un determinato sistema di coordinate 3D e una lunghezza di 5 unità, possiamo scrivere il vettore come segue:
$$\mathbf{\vec v} = <5, 0, 0>$$Per rappresentare tale vettore, occorre un punto di ancoraggio nel sistema di coordinate. Ad esempio, tutte le frecce della figura seguente sono rappresentazioni uguali dello stesso vettore, nonostante siano ancorate in diversi punti.
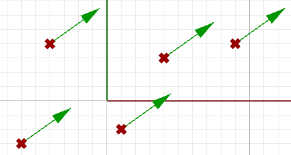
Quindi, come possiamo definire i punti di fine del segmento di una retta che rappresenta un determinato vettore? Definiamo un punto di ancoraggio (A) in questo modo:
$$A = (1, 2, 3)$$E un vettore:
$$\mathbf{\vec v} = <5, 6, 7>$$La punta $$(B)$$ del vettore viene calcolata sommando i componenti corrispondenti dal punto di ancoraggio e dal vettore $$\vec v$$:
$$B = A + \mathbf{\vec v}$$
$$B = (1+5, 2+6, 3+7) $$
$$B = (6, 8, 10)$$
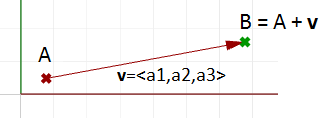
Vettore posizione
La rappresentazione di un particolare vettore utilizza il punto di origine $$\text{origin point} (0,0,0)$$ come punto di ancoraggio del vettore. Il vettore posizione $$\mathbf{\vec v} = <a_1,a_2,a_3>$$ è rappresentato con un segmento di linea fra due punti, l’origine e B, quindi:
$$\text{Origin point} = (0,0,0)$$
$$B = (a_1,a_2,a_3)$$
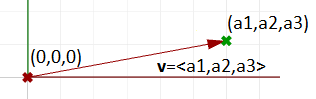
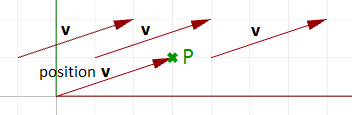
Vettori e punti
Non confondere vettori e punti. Sono concetti molto diversi. Come menzionato, i vettori rappresentano una quantità con una direzione e lunghezza, mentre i punti indicano una posizione. Ad esempio, la direzione nord è un vettore mentre il polo nord è una pozione (punto). Se abbiamo un vettore e un punto che presentano gli stessi componenti, come:
$$\mathbf{\vec v} = <3,1,0>$$
$$P = (3,1,0)$$
Possiamo disegnare il vettore e il punto come segue:
Lunghezza del vettore
Come indicato in precedenza, i vettori presentano una lunghezza. Utilizzeremo $$\vert a \vert$$ per indicare la lunghezza di un determinato vettore $$ a $$. Per esempio:
$$\mathbf{\vec a} = <4, 3, 0>$$
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5$$
In generale, la lunghezza di un vettore $$\mathbf{\vec a} <a_1,a_2,a_3>$$ viene calcolata come segue:
$$\vert \mathbf{\vec a} \vert = \sqrt{(a_1)^2 + (a_2)^2 + (a_3)^2} $$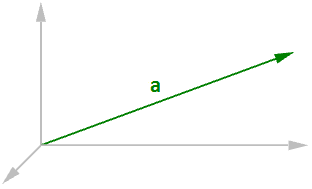
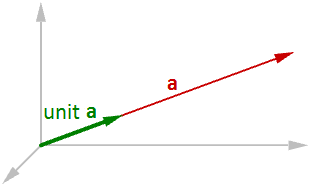
Vettore di unità
Un vettore di unità è un vettore con una lunghezza uguale a una unità. I vettori di unità sono comunemente usati per mettere a confronto le direzioni dei vettori.
Per calcolare un vettore di unità, occorre trovare la lunghezza di un determinato vettore e quindi dividere i componenti del vettore per la lunghezza. Per esempio:
$$\mathbf{\vec a} = <4, 3, 0>$$
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5 \text{ unit length}$$
If
$$\mathbf{\vec b} = \text{unit vector}$$ of
$$a$$, then:
$$\mathbf{\vec b} = <4/5, 3/5, 0/5>$$
$$\mathbf{\vec b} = <0.8, 0.6, 0>$$
$$\vert \mathbf{\vec b} \vert = \sqrt{0.8^2 + 0.6^2 + 0^2}$$
$$\vert \mathbf{\vec b} \vert = \sqrt{0.64 + 0.36 + 0}$$
$$\vert \mathbf{\vec b} \vert = \sqrt{(1)} = 1 \text{ unit length}$$
In generale:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$Il vettore unitario di $$\mathbf{\vec a} = <a_1/\vert \mathbf{\vec a} \vert , a_2/\vert \mathbf{\vec a} \vert , a_3/\vert \mathbf{\vec a} \vert >$$
1.2 Operazioni vettoriali
Operazione scalare di un vettore
L’operazione scalare di un vettore implica moltiplicare un vettore per un numero. Per esempio:
$$\mathbf{\vec a} = <4, 3, 0>$$
$$2* \mathbf{\vec a} = <24, 23, 2*0> $$
$$2*\mathbf{\vec a} = <8, 6, 0>$$
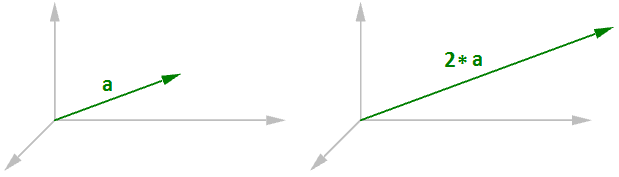
In generale, dato un vettore $$\mathbf{\vec a} = <a_1, a_2, a_3>$$ e un numero reale $$t$$
$$t*\mathbf{\vec a} = < t* a_1, t* a_2, t* a_3 >$$Somma vettoriale
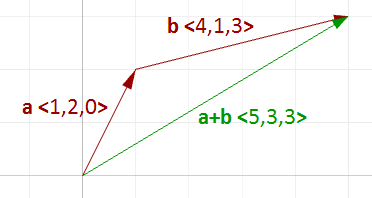
La somma vettoriale coinvolge due vettori e ne crea un terzo. Sommiamo i vettori sommando i loro componenti.
Ad esempio, se abbiamo due vettori:
$$\mathbf{\vec a} = <1, 2, 0> $$
$$\mathbf{\vec b} = <4, 1, 3> $$
$$\mathbf{\vec a} = <+4, +1, 0>$$
$$\mathbf{\vec a}+\mathbf{\vec b} = <5, 3, 3>$$
In generale, la somma vettoriale dei due vettori a e b viene calcolata come segue:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a}+\mathbf{\vec b} = <a_1+b_1, a_2+b_2, a_3+b_3>$$
La somma vettoriale è utile per trovare la direzione media di due o più vettori. In questo caso, usiamo di solito vettori della stessa lunghezza. Ecco un esempio che mostra la differenza fra usare vettori della stessa lunghezza e vettori di lunghezza diversa nella somma vettoriale che ne risulta:
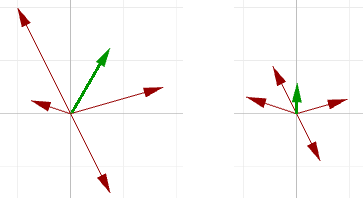
I vettori di input non sono probabilmente della stessa lunghezza. Per trovare la direzione media, occorre usare il vettore di unità dei vettori di input. Come menzionato in precedenza, il vettore di unità è un vettore con lunghezza pari a 1.
Sottrazione vettoriale
La sottrazione vettoriale coinvolge due vettori e ne crea un terzo. Sottraiamo due vettori sottraendo i componenti corrispondenti. Ad esempio, se abbiamo due vettori $$\mathbf{\vec a}$$ e $$\mathbf{\vec b}$$ e sottraiamo $$\mathbf{\vec b}$$ da $$\mathbf{\vec a}$$, allora:
$$\mathbf{\vec a} = <1, 2, 0> $$
$$\mathbf{\vec b} = <4, 1, 4> $$
$$\mathbf{\vec a}-\mathbf{\vec b} = <1-4, 2-1, 0-4>$$
$$\mathbf{\vec a}-\mathbf{\vec b} = <-3, 1, -4> = \mathbf{\mathbf{\vec b}a}$$
Se si sottrae $$\mathbf{\vec b}$$ da $$\mathbf{\vec a}$$, otteniamo un risultato diverso:
$$\mathbf{\vec b} - \mathbf{\vec a} = <4-1, 1-2, 4-0>$$
$$\mathbf{\vec b} - \mathbf{\vec a} = <3, -1, 4> = \mathbf{\mathbf{\vec a}b}$$
Nota: il vettore $$\mathbf{\vec b} - \mathbf{\vec a}$$ presenta la stessa lunghezza del vettore $$\mathbf{\vec a} - \mathbf{\vec b}$$, ma va nella direzione opposta.
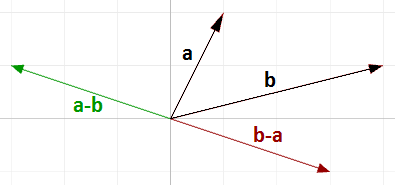
In generale, se abbiamo due vettori, $$\mathbf{\vec a}$$ and $$\mathbf{\vec b}$$, then $$\mathbf{\vec a} - \mathbf{\vec b}$$ è un vettore che viene calcolato come segue:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a}-\mathbf{\vec b} = <a_1 - b_1, a_2 - b_2, a_3 - b_3> = \mathbf{\mathbf{\vec b}a}$$
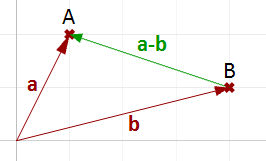
La sottrazione vettoriale è comunemente usata per trovare vettori fra punti. Per trovare un vettore che va dalla punta al vettore posizione $$\mathbf{\vec b}$$ alla punta del vettore posizione $$\mathbf{\vec a}$$, usiamo quindi la sottrazione $$(\mathbf{\vec a}-\mathbf{\vec b})$$ come mostrato nella figura (11).
Proprietà vettoriali
I vettori presentano otto proprietà. Se a, b e c sono vettori ed s e t sono numeri, allora:
$$\mathbf{\vec a} + \mathbf{\vec b} = \mathbf{\vec b} + \mathbf{\vec a}$$
$$\mathbf{\vec a} + 0 = a$$
$$s * (\mathbf{\vec a} + \mathbf{\vec b}) = s * a + s * \mathbf{\vec b}$$
$$s * t * (\mathbf{\vec a}) = s * (t * \mathbf{\vec a})$$
$$\mathbf{\vec a} + (\mathbf{\vec b} + \mathbf{\vec c}) = (\mathbf{\vec a} + \mathbf{\vec b}) + \mathbf{\vec c}$$
$$\mathbf{\vec a} + (-\mathbf{\vec a}) = 0$$
$$(s + t) * \mathbf{\vec a} = s * \mathbf{\vec a} + t * \mathbf{\vec a}$$
$$1 * \mathbf{\vec a} = \mathbf{\vec a}$$
Prodotto scalare del vettore
Il prodotto scalare coinvolge due vettori e crea un numero. Ad esempio, se abbiamo due vettori a e b, allora:
$$\mathbf{\vec a} = <1, 2, 3> $$
$$\mathbf{\vec b} = <5, 6, 7>$$
Quindi, il prodotto scalare è la somma della moltiplicazione dei componenti, come segue:
$$\mathbf{\vec a} · \mathbf{\vec b} = 1 * 5 + 2 * 6 + 3 * 7$$
$$\mathbf{\vec a} · \mathbf{\vec b} = 38$$
In generale, dati due vettori a e b:
$$\mathbf{\vec a} = <a_1, a_2, a_3>$$
$$\mathbf{\vec b} = <b_1, b_2, b_3>$$
$$\mathbf{\vec a} · \mathbf{\vec b} = a_1 * b_1 + a_2 * b_2 + a_3 * b_3$$
Otteniamo sempre un numero positivo per il prodotto scalare fra due vettori quando vanno nella stessa direzione generale. Un prodotto scalare fra due vettori indica che i due vettori vanno nella direzione generale opposta.
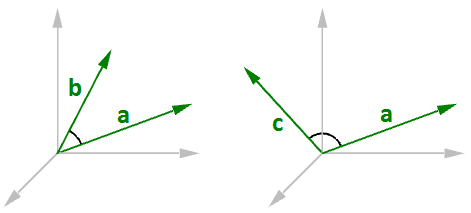
Quando calcoliamo il prodotto scalare di due vettori di unità, il risultato è sempre compreso fra 1 e +1. Per esempio:
$$\mathbf{\vec a} = <1, 0, 0>$$
$$\mathbf{\vec b} = <0.6, 0.8, 0>$$
$$\mathbf{\vec a} · \mathbf{\vec b} = (1 * 0.6, 0 * 0.8, 0 * 0) = 0.6$$
Inoltre, il prodotto scalare di un vettore in sé è uguale alla lunghezza di tale vettore secondo il potere di due. Per esempio:
$$\mathbf{\vec a} = <0, 3, 4>$$
$$\mathbf{\vec a} · \mathbf{\vec a} = 0 * 0 + 3 * 3 + 4 * 4 $$
$$\mathbf{\vec a} · \mathbf{\vec a} = 25$$
Calcolare la lunghezza della radice quadrata di un vettore $$\mathbf{\vec a}$$ :
$$\vert \mathbf{\vec a} \vert = \sqrt{4^2 + 3^2 + 0^2}$$
$$\vert \mathbf{\vec a} \vert = 5$$
$$\vert \mathbf{\vec a} \vert 2 = 25$$
Prodotto scalare del vettore, lunghezze e angoli
Esiste un rapporto fra il prodotto scalare di due vettori e l’angolo fra di loro.
In generale:
$$\mathbf{\vec a} · \mathbf{\vec b} = \vert \mathbf{\vec a} \vert * \vert \mathbf{\vec b} \vert * cos(ө)$$ oppure
$$\mathbf{\vec a} · \mathbf{\vec b} / (\vert \mathbf{\vec a} \vert * \vert \mathbf{\vec b} \vert) = cos(ө)$$
Dove:
$$ө$$ è l’angolo incluso fra i vettori.
Se i vettori a e b sono vettori di unità, possiamo affermare che:
$$\mathbf{\vec a} · \mathbf{\vec b} = cos(ө)$$E poiché il coseno di un angolo di 90 gradi è uguale a 0, possiamo affermare che:
Ad esempio, se calcoliamo il prodotto scalare di due vettori ortogonali, l’asse X e l’asse Y del sistema assoluto, il risultato sarà uguale a zero.
$$\mathbf{\vec x} = <1, 0, 0>$$
$$\mathbf{\vec y} = <0, 1, 0>$$
x · y = (1 * 0) + (0 * 1) + (0 * 0)
$$\mathbf{\vec x} · \mathbf{\vec y} = 0$$
Esiste inoltre un rapporto fra il prodotto scalare e la lunghezza della proiezione di un vettore su un altro. Per esempio:
$$\mathbf{\vec a} = <5, 2, 0>$$
$$\mathbf{\vec b} = <9, 0, 0>$$
$$unit(\mathbf{\vec b}) = <1, 0, 0>$$
$$\mathbf{\vec a} · unit(\mathbf{\vec b}) = (5 * 1) + (2 * 0) + (0 * 0) $$
$$\mathbf{\vec a} · unit(\mathbf{\vec b}) = 2 (\text{which is equal to the projection length of mathbf{\vec a} onto mathbf{\vec b}})$$

In generale, dato un vettore a e un vettore diverso da zero b, possiamo calcolare la lunghezza della proiezione pL del vettore a sul vettore b usando il prodotto scalare.
$$pL = \vert \mathbf{\vec a} \vert * cos(ө) $$
$$pL = \mathbf{\vec a} · unit(\mathbf{\vec b})$$
Proprietà del prodotto scalare
Se $$\mathbf{\vec a}$$, $$\mathbf{\vec b}$$ e $$\mathbf{\vec c}$$ sono vettori e s è un numero, allora:
$$\mathbf{\vec a} · \mathbf{\vec a} = \vert \mathbf{\vec a} \vert ^2$$
$$\mathbf{\vec a} · (\mathbf{\vec b} + \mathbf{\vec c}) = \mathbf{\vec a} · \mathbf{\vec b} + \mathbf{\vec a} · \mathbf{\vec c}$$
$$0 · \mathbf{\vec a} = 0$$
$$\mathbf{\vec a} · \mathbf{\vec b} = \mathbf{\vec b} · \mathbf{\vec a}$$
$$(s * \mathbf{\vec a}) · \mathbf{\vec b} = s * (\mathbf{\vec a} · \mathbf{\vec b}) = \mathbf{\vec a} · (s * \mathbf{\vec b})$$
Prodotto vettoriale
Il prodotto vettoriale coinvolge due vettori e ne crea un terzo che è ortogonale a entrambi.
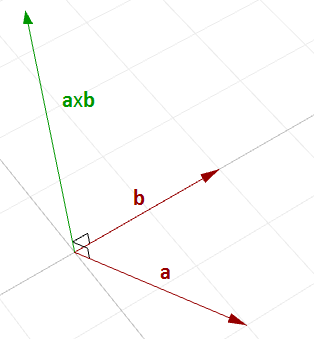
Ad esempio, se abbiamo due vettori su un piano assoluto XY, il loro prodotto vettoriale è un vettore perpendicolare al piano XY, che va sia nella direzione positiva che negativa dell’asse Z. Per esempio:
$$\mathbf{\vec a} = <3, 1, 0>$$
$$\mathbf{\vec b} = <1, 2, 0>$$
$$\mathbf{\vec a} × \mathbf{\vec b} = < (1 * 0 – 0 * 2), (0 * 1 - 3 * 0), (3 * 2 - 1 * 1) > $$
$$\mathbf{\vec a} × \mathbf{\vec b} = <0, 0, 5>$$
Probabilmente, non sarà necessario calcolare manualmente il prodotto vettoriale di due vettori, quindi è possibile ignorare questa sezione. Gli utenti interessati al calcolo del prodotto vettoriale possono continuare a leggere per un maggiore approfondimento. Il prodotto vettoriale $$a × b$$ viene definito usando determinanti. Ecco una semplice illustrazione su come calcolare un determinante usando i vettori di base standard:
$$ \color {red}{i} = <1, 0, 0>$$
$$ \color {blue}{j} = <0,1, 0>$$
$$ \color {green}{k} = <0, 0, 1>$$
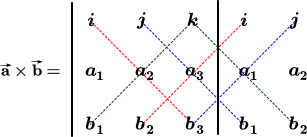
Il prodotto vettoriale di due vettori $$\mathbf{\vec a} = <a1, a2, a3>$$ e $$\mathbf{\vec b} = <b1, b2, b3>$$ viene calcolato come segue usando il diagramma precedente:
$$\mathbf{\vec a} × \mathbf{\vec b} = \color {red}{i (a_2 * b_3)} + \color {blue}{ j (a_3 * b_1)} + \color {green}{k(a_1 * b_2)} - \color {green}{k (a_2 * b_1)} - \color {red}{i (a_3 * b_2)} -\color {blue}{ j (a_1 * b_3)}$$
$$\mathbf{\vec a} × \mathbf{\vec b} = \color {red}{i (a_2 * b_3 - a_3 * b_2)} + \color {blue}{j (a_3 * b_1 - a_1 * b_3)} +\color {green}{k (a_1 * b_2 - a_2 * b_1)}$$
$$\mathbf{\vec a} × \mathbf{\vec b} = <\color {red}{a_2 * b_3 – a_3 * b_2}, \color {blue}{a_3 * b_1 - a_1 * b_3}, \color {green}{a_1 * b_2 - a_2 * b_1} >$$
Prodotto vettoriale e angolo fra vettori
Esiste un rapporto fra l’angolo, fra i due vettori e la lunghezza del prodotto vettoriale. Quanto più piccolo è l’angolo (seno più piccolo), tanto minore sarà il prodotto vettoriale. L’ordine degli operandi è importante nel prodotto vettoriale. Per esempio:
$$\mathbf{\vec a} = <1, 0, 0>$$
$$\mathbf{\vec b} = <0, 1, 0>$$
$$\mathbf{\vec a} × \mathbf{\vec b} = <0, 0, 1>$$
$$\mathbf{\vec b} × \mathbf{\vec a} = <0, 0, -1>$$
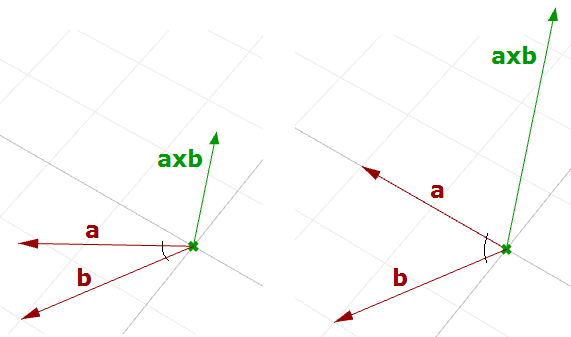
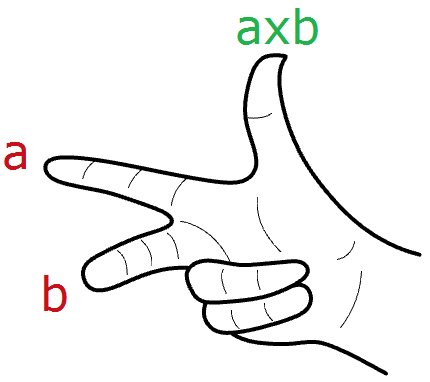
Nel sistema destrorso di Rhino, la direzione di $$\mathbf{\vec a} × \mathbf{\vec b}$$ è data dalla regola della mano destra (dove $$\mathbf{\vec a}$$ = dito indice, $$\mathbf{\vec b}$$ = dito medio e $$\mathbf{\vec a} × \mathbf{\vec b}$$ = pollice).
In generale, per qualsiasi paio di vettori 3D $$\mathbf{\vec a}$$ and $$\mathbf{\vec b}$$:
$$\vert \mathbf{\vec a} × \mathbf{\vec b} \vert = \vert \mathbf{\vec a} \vert \vert \mathbf{\vec b} \vert sin(ө)$$Dove:
$$Ө$$ è l’angolo compreso tra i vettori posizione di $$\mathbf{\vec a}$$ and $$\mathbf{\vec b}$$
Se a e b sono vettori di unità, possiamo quindi affermare semplicemente che la lunghezza del loro prodotto vettoriale è uguale al seno dell’angolo fra di loro. In altre parole:
$$\vert \mathbf{\vec a} × \mathbf{\vec b} \vert = sin(ө)$$Il prodotto vettoriale fra due vettori ci aiuta a determinare se due vettori sono paralleli. Ciò è dovuto al risultato che è sempre un vettore uguale a zero.
Proprietà del prodotto vettoriale
Se
$$\mathbf{\vec a}$$,
$$\mathbf{\vec b}$$ e
$$\mathbf{\vec c}$$ sono vettori e
$$s$$ è un numero, allora:
$$\mathbf{\vec a} × \mathbf{\vec b} = -\mathbf{\vec b} × \mathbf{\vec a}$$
$$(s * \mathbf{\vec a}) × \mathbf{\vec b} = s * (\mathbf{\vec a} × \mathbf{\vec b}) = \mathbf{\vec a} × (s * \mathbf{\vec b})$$
$$\mathbf{\vec a} × (\mathbf{\vec b} + \mathbf{\vec c}) = \mathbf{\vec a} × \mathbf{\vec b} + \mathbf{\vec a} × \mathbf{\vec c}$$
$$(\mathbf{\vec a} + \mathbf{\vec b}) × \mathbf{\vec c} = \mathbf{\vec a} × \mathbf{\vec c} + \mathbf{\vec b} × \mathbf{\vec c}$$
$$\mathbf{\vec a} · (\mathbf{\vec b} × \mathbf{\vec c}) = (\mathbf{\vec a} × \mathbf{\vec b}) · \mathbf{\vec c}$$
$$\mathbf{\vec a} × (\mathbf{\vec b} × \mathbf{\vec c}) = (\mathbf{\vec a} · \mathbf{\vec c}) * \mathbf{\vec b} – (\mathbf{\vec a} · \mathbf{\vec b}) * \mathbf{\vec c}$$
1.3 Equazione vettoriale di una retta
L’equazione vettoriale di una retta è usata nelle applicazioni di modellazione 3D e computer grafica.
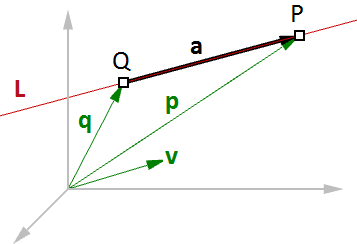
Ad esempio, se conosciamo la direzione di una retta e di un punto su tale retta, allora possiamo trovare qualsiasi altro punto sulla retta usando i vettori, come di seguito:
$$\overline{L} = line$$
$$\mathbf{\vec v} = <a, b, c>$$ vettore unitario di direzione della retta
$$Q = (x_0, y_0, z_0)$$ punto di posizione della retta
$$P = (x, y, z)$$ qualsiasi punto sulla retta
Sappiamo che:
$$\mathbf{\vec a} = t *\mathbf{\vec v}$$ (2)
$$\mathbf{\vec p} = \mathbf{\vec q} + \mathbf{\vec a}$$ (1)
Da 1 e 2:
$$\mathbf{\vec p} = \mathbf{\vec q} + t * \mathbf{\vec v}$$ (3)
Tuttavia, possiamo scrivere (3) quanto segue:
$$<x, y, z> = <x_0, y_0, z_0> + <t * a, t * b, t * c>$$
$$<x, y, z> = <x_0 + t * a, y_0 + t * b, z_0 + t * c>$$
Quindi:
$$x = x_0 + t * a$$
$$y = y_0 + t * b$$
$$z = z_0 + t * c$$
Che equivale a:
$$P = Q + t * \mathbf{\vec v}$$Un altro esempio comune è trovare un punto medio fra due punti. L’esempio seguente mostra come trovare il punto medio usando l’equazione vettoriale di una retta:
$$\mathbf{\vec q}$$ è il vettore posizione per il punto
$$Q$$
$$\mathbf{\vec p}$$ è il vettore posizione per il punto
$$P$$
$$\mathbf{\vec a}$$ è il vettore che va da
$$Q \rightarrow P$$
Della sottrazione vettoriale, sappiamo che:
$$\mathbf{\vec a} = \mathbf{\vec p} - \mathbf{\vec q}$$Dell’equazione della retta, sappiamo che:
$$M = Q + t * \mathbf{\vec a}$$E visto che dobbiamo trovare un punto medio, allora:
$$t = 0.5$$Possiamo quindi affermare che:
$$M = Q + 0.5 * \mathbf{\vec a}$$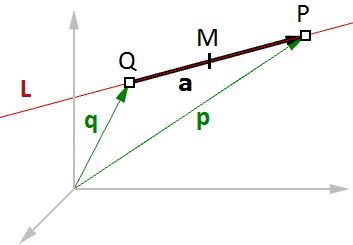
In generale, è possibile trovare qualsiasi punto fra $$Q$$ e $$P$$ cambiando il valore $$t$$ fra 0 e 1 usando l’equazione generale:
$$M = Q + t * (P - Q)$$$$Q$$ e $$P$$, qualsiasi punto $$M$$ fra due punti viene calcolato usando l’equazione $$M = Q + t * (P - Q)$$ dove t è un numero compreso fra 0 e 1.
1.4 Equazione vettoriale di un piano
Un modo per definire un piano è usare un punto e un vettore perpendicolare al piano. Il riferimento di tale vettore è di solito la normale al piano. La normale punta nella direzione al di sopra del piano.
Un esempio di come calcolare la normale a un piano è conoscere tre punti non lineari sul piano.
La figura (16) mostra quanto segue:
$$A$$ = il primo punto sul piano.
$$B$$ = il secondo punto sul piano.
$$C$$ = il terzo punto sul piano.
E:
$$\mathbf{\vec a} $$ = vettore posizione di un punto
$$A$$
$$\mathbf{\vec b}$$ = vettore posizione di un punto
$$B$$
$$\mathbf{\vec c}$$ = vettore posizione di un punto
$$C$$
Possiamo trovare il vettore normale $$\mathbf{\vec n}$$ come segue:
$$\mathbf{\vec n} = (\mathbf{\vec b} - \mathbf{\vec a}) × (\mathbf{\vec c} - \mathbf{\vec a})$$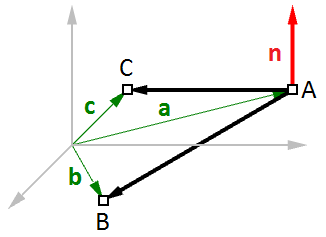
Possiamo anche derivare l’equazione scalare del piano usando il prodotto scalare:
$$\mathbf{\vec n} · (\mathbf{\vec b} - \mathbf{\vec a}) = 0$$Se:
$$\mathbf{\vec n} = <a, b, c>$$
$$\mathbf{\vec b} = <x, y, z>$$
$$ \mathbf{\vec a} = <x_0, y_0, z_0>$$
Possiamo quindi ampliare quanto indicato precedentemente:
$$<a, b, c> · <x-x_0, y-y_0, z-z_0 > = 0$$Risolvendo il prodotto scalare, otteniamo l’equazione scalare generale di un piano:
$$a * (x - x_0) + b * (y - y_0) + c * (z - z_0) = 0$$1.5 Tutorial
Tutti i concetti spiegati in questo capitolo hanno applicazione diretta nella risoluzione dei comuni problemi di geometria riscontrati durante la modellazione. I seguenti tutorial spiegano passo a passo come usare i concetti appresi in Rhinoceros e Grasshopper (GH).
1.5.1 Direzione delle facce
Dato un punto e una superficie, come possiamo determinare se il punto è rivolto verso il lato anteriore o posteriore della superficie?
Input:
- Una superficie.
- Un punto.
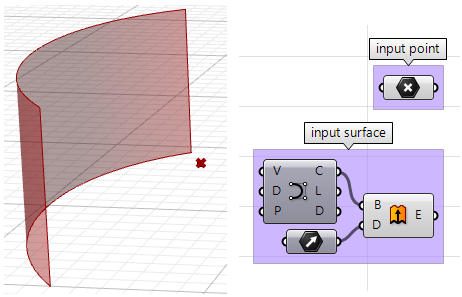
Parametri:
La direzione è definita dalla direzione alla normale della superficie. Saranno necessarie le seguenti informazioni:
- La direzione della normale al punto della superficie più vicino al punto di input.
- La direzione vettoriale dal punto più vicino al punto di input.
Confronta le due direzioni indicate sopra, se vanno nella stessa direzione, il punto è rivolto verso il lato anteriore altrimenti è rivolto verso il lato posteriore.
Soluzione:
1. Trova la posizione del punto più vicino sulla superficie relativo al punto di input usando il componente Pull. In questo modo, troveremo la posizione uv del punto più vicino, utile per valutare la superficie e trovarne le direzioni alla normale.
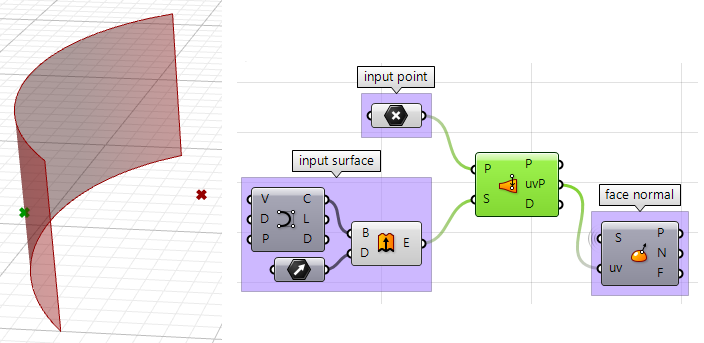
2. Possiamo ora usare il punto più vicino per disegnare un vettore che va verso il punto di input. Possiamo anche disegnare quanto segue:
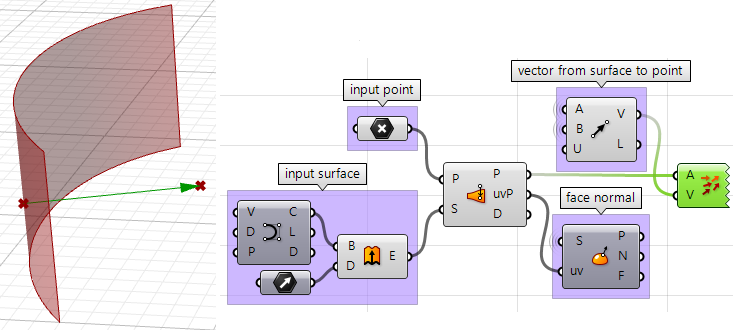
3. Possiamo confrontare i due vettori usando il prodotto scalare. Se il risultato è positivo, il punto è di fronte alla superficie. Se il risultato è negativo, il punto si trova dietro la superficie.
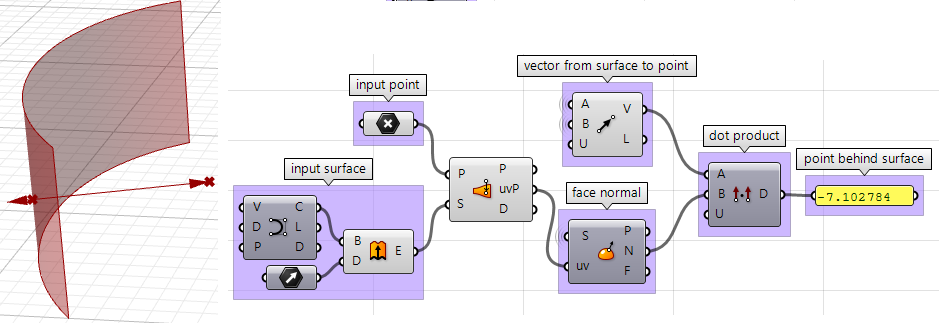
I passi sopra indicati possono anche essere eseguiti usando altri linguaggi di scripting. Usare il componente VB per Grasshopper:
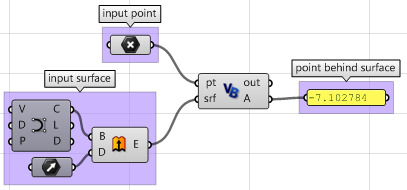
Private Sub RunScript(ByVal pt As Point3d, ByVal srf As Surface, ByRef A As Object)
'Declare variables
Dim u, v As Double
Dim closest_pt As Point3d
'get closest point u, v
srf.ClosestPoint(pt, u, v)
'get closest point
closest_pt = srf.PointAt(u, v)
'calculate direction from closest point to test point
Dim dir As New Vector3d(pt - closest_pt)
'calculate surface normal
Dim normal = srf.NormalAt(u, v)
'compare the two directions using the dot product
A = dir * normal
End Sub
Usare il componente Grasshopper Python con RhinoScriptSyntax:
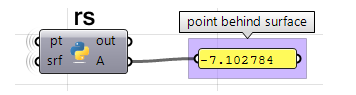
import rhinoscriptsyntax as rs #import RhinoScript library
#find the closest point
u, v = rs.SurfaceClosestPoint(srf, pt)
#get closest point
closest_pt = rs.EvaluateSurface(srf, u, v)
#calculate direction from closest point to test point
dir = rs.PointCoordinates(pt) - closest_pt
#calculate surface normal
normal = rs.SurfaceNormal(srf, [u, v])
#compare the two directions using the dot product
A = dir * normal
Usare il componente Grasshopper Python solo con RhinoCommon:
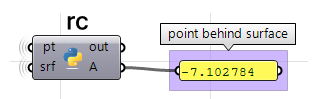
#find the closest point
found, u, v = srf.ClosestPoint(pt)
if found:
#get closest point
closest_pt = srf.PointAt(u, v)
#calculate direction from closest point to test point
dir = pt - closest_pt
#calculate surface normal
normal = srf.NormalAt(u, v)
#compare the two directions using the dot product
A = dir * normal
Usare il componente C# per Grasshopper:

private void RunScript(Point3d pt, Surface srf, ref object A)
{
//Declare variables
double u, v;
Point3d closest_pt;
//get closest point u, v
srf.ClosestPoint(pt, out u, out v);
//get closest point
closest_pt = srf.PointAt(u, v);
//calculate direction from closest point to test point
Vector3d dir = pt - closest_pt;
//calculate surface normal
Vector3d normal = srf.NormalAt(u, v);
//compare the two directions using the dot product
A = dir * normal;
}
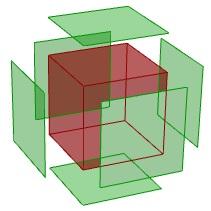
1.5.2 Esplodere un parallelepipedo
Il seguente tutorial mostra come esplodere una polisuperficie. Il parallelepipedo esploso ha il seguente aspetto:
Input:
Identifica l’input che corrisponde a un parallelepipedo. Useremo il parametro Box in GH:

Parametri:
- Considera tutti i parametri necessari per seguire questo tutorial.
- Il centro dell’esplosione.
- Le facce del parallelepipedo da esplodere.
- La direzione verso cui si sposta ciascuna faccia.
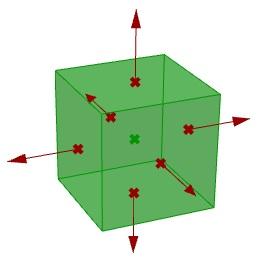
Una volta identificati i parametri, si tratta di metterli insieme per trovare una soluzione in base a passi logici che conducono alla risposta.
Soluzione:
1. Trovare il centro del parallelepipedo usando il componente Box Properties in GH:
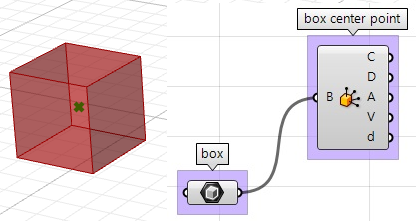
2. Estrarre le facce del parallelepipedo con il componente Deconstruct Brep:
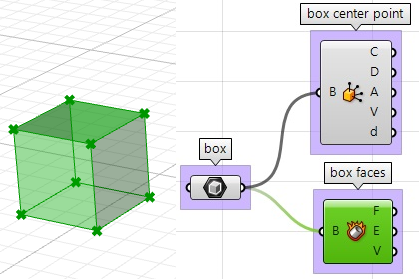
3. La parte più difficile riguarda la direzione verso cui spostiamo le facce. Anzitutto, occorre trovare il centro di ciascuna faccia, quindi definire la direzione dal centro del parallelepipedo verso il centro di ciascuna faccia, come segue:
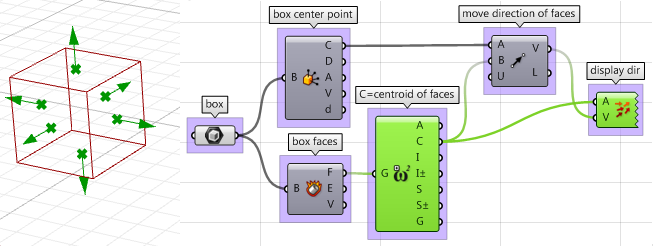
4. Una volta eseguito lo script per tutti i parametri, possiamo usare il componente Move per spostare le facce nella direzione appropriata. Assicurati di impostare i vettori sull’ampiezza desiderata.
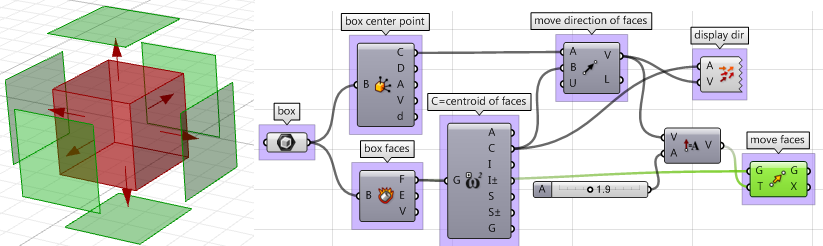
I passi sopra indicati possono essere eseguiti usando scripting VB, C# o Python. Di seguito, la soluzione usando i tre linguaggi di scripting.
Usare il componente VB per Grasshopper:
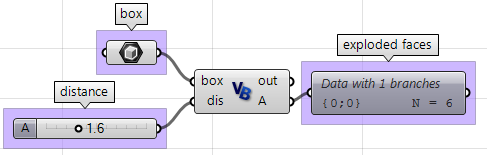
Private Sub RunScript(ByVal box As Brep, ByVal dis As Double, ByRef A As Object)
'get the brep center
Dim area As Rhino.Geometry.AreaMassProperties
area = Rhino.Geometry.AreaMassProperties.Compute(box)
Dim box_center As Point3d
box_center = area.Centroid
'get a list of faces
Dim faces As Rhino.Geometry.Collections.BrepFaceList = box.Faces
'decalre variables
Dim center As Point3d
Dim dir As Vector3d
Dim exploded_faces As New List( Of Rhino.Geometry.Brep )
Dim i As Int32
'loop through all faces
For i = 0 To faces.Count() - 1
'extract each of the face
Dim extracted_face As Rhino.Geometry.Brep = box.Faces.ExtractFace(i)
'get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face)
center = area.Centroid
'calculate move direction (from box centroid to face center)
dir = center - box_center
dir.Unitize()
dir *= dis
'move the extracted face
extracted_face.Transform(Transform.Translation(dir))
'add to exploded_faces list
exploded_faces.Add(extracted_face)
Next
'assign exploded list of faces to output
A = exploded_faces
End Sub
Usare il componente Grasshopper Python con RhinoCommon:
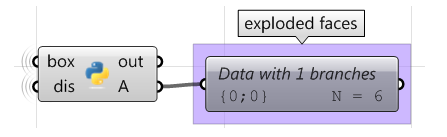
import Rhino
#get the brep center
area = Rhino.Geometry.AreaMassProperties.Compute(box)
box_center = area.Centroid
#get a list of faces
faces = box.Faces
#decalre variables
exploded_faces = []
#loop through all faces
for i, face in enumerate(faces):
#get a duplicate of the face
extracted_face = faces.ExtractFace(i)
#get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face)
center = area.Centroid
#calculate move direction (from box centroid to face center)
dir = center - box_center
dir.Unitize()
dir *= dis
#move the extracted face
move = Rhino.Geometry.Transform.Translation(dir)
extracted_face.Transform(move)
#add to exploded_faces list
exploded_faces.append(extracted_face)
#assign exploded list of faces to output
A = exploded_faces
Usare il componente C# per Grasshopper:
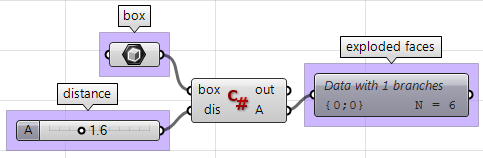
private void RunScript(Brep box, double dis, ref object A)
{
//get the brep center
Rhino.Geometry.AreaMassProperties area = Rhino.Geometry.AreaMassProperties.Compute(box);
Point3d box_center = area.Centroid;
//get a list of faces
Rhino.Geometry.Collections.BrepFaceList faces = box.Faces;
//decalre variables
Point3d center; Vector3d dir;
List<Rhino.Geometry.Brep> exploded_faces = new List<Rhino.Geometry.Brep>();
//loop through all faces for( int i = 0; i < faces.Count(); i++ )
{
//extract each of the face
Rhino.Geometry.Brep extracted_face = box.Faces.ExtractFace(i);
//get the center of each face
area = Rhino.Geometry.AreaMassProperties.Compute(extracted_face);
center = area.Centroid;
//calculate move direction (from box centroid to face center)
dir = center - box_center;
dir.Unitize();
dir *= dis;
//move the extracted face
extracted_face.Transform(Transform.Translation(dir));
//add to exploded_faces list
exploded_faces.Add(extracted_face);
}
//assign exploded list of faces to output
A = exploded_faces;
}
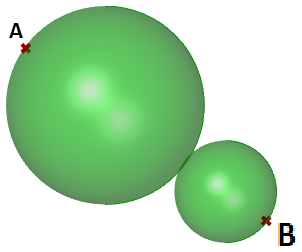
1.5.3 Sfere tangenti
Questo tutorial mostra come creare due sfere tangenti fra due punti di input. Ecco come appare il risultato:
Input:
Due punti (
$$A$$ e
$$B$$) nel sistema di coordinate 3D.
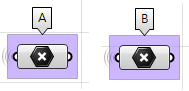
Parametri: Di seguito, un diagramma dei parametri necessari per risolvere il problema: $$A$$ punto tangente $$D$$ fra le due sfere, nel parametro $$t$$ (0-1) tra i punti $$A$$ e $$B$$.
- Il centro della prima sfera o il punto medio $$C1$$ fra $$A$$ e $$D$$.
- Il centro della seconda sfera o il punto medio $$C2$$ fra $$D$$ e $$B$$.
- Il raggio della prima sfera $$(r1)$$ o la distanza fra $$A$$ e $$C1$$.
- Il raggio della seconda sfera $$(r2)$$ o la distanza fra $$D$$ e $$C2$$.
Soluzione:
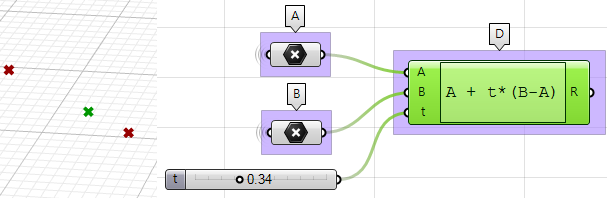
1. Utilizzare il componente Expression per definire il punto $$D$$ fra $$A$$ e $$B$$ in un parametro $$t$$. L’espressione che useremo si basa sull’equazione vettoriale di una retta:
$$D = A + t*(B-A)$$$$B-A$$ : è il vettore che va da $$B$$ a
$$A (\vec{BA}) usando l’operazione di sottrazione.
$$
t*(B-A) $$ : dove $$t$$ è compreso fra 0 e 1 per ottenere una posizione sul vettore.
$$
A+t*(B-A)$$ : ottiene un punto sul vettore A e B.
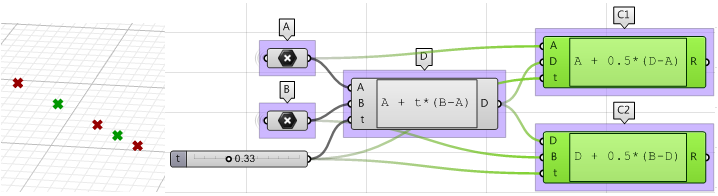
2. Usa il componente Expression per definire inoltre i punti medi $$
C1 $$ e $$C2$$.
3. Il raggio della prima sfera $$
(r1) $$ e il raggio della seconda sfera $$(r2)$$ possono essere calcolati usando il componente Distance.
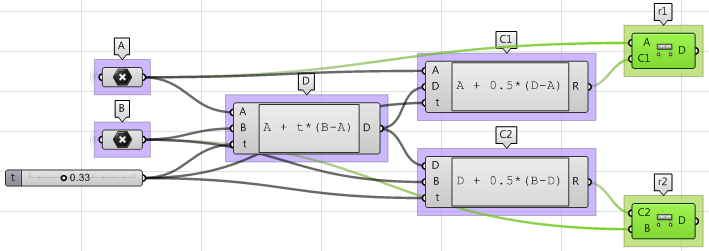
4. Il passo finale implica la creazione della sfera da un piano di base e un raggio. Occorre assicurarsi che le origini siano collegate a $$
C1 $$ e $$C2 $$ e il raggio da $$r1 $$ e $$r2$$.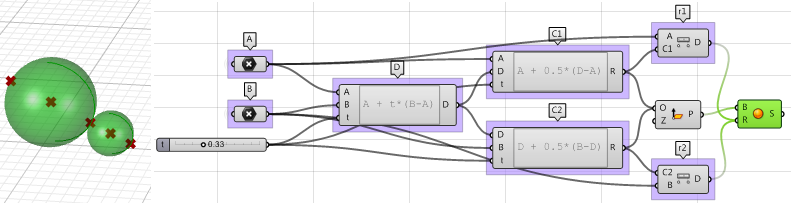
Usare il componente VB per Grasshopper:
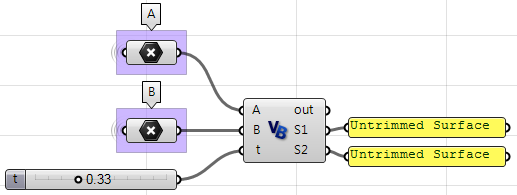
Private Sub RunScript(ByVal A As Point3d, ByVal B As Point3d, ByVal t As Double, ByRef S1 As Object, ByRef S2 As Object)
'declare variables
Dim D, C1, C2 As Rhino.Geometry.Point3d
Dim r1, r2 As Double
'find a point between A and B
D = A + t * (B - A)
'find mid point between A and D
C1 = A + 0.5 * (D - A)
'find mid point between D and B
C2 = D + 0.5 * (B - D)
'find spheres radius
r1 = A.DistanceTo(C1)
r2 = B.DistanceTo(C2)
'create spheres and assign to output
S1 = New Rhino.Geometry.Sphere(C1, r1)
S2 = New Rhino.Geometry.Sphere(C2, r2)
End Sub
Usare il componente Python:
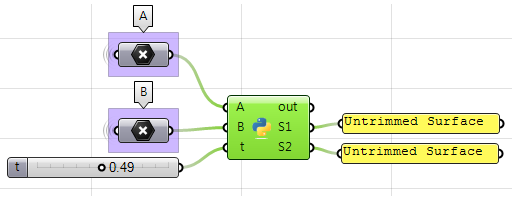
import Rhino
#find a point between A and B
D = A + t * (B - A)
#find mid point between A and D
C1 = A + 0.5 * (D - A)
#find mid point between D and B
C2 = D + 0.5 * (B - D)
#find spheres radius
r1 = A.DistanceTo(C1)
r2 = B.DistanceTo(C2)
#create spheres and assign to output
S1 = Rhino.Geometry.Sphere(C1, r1)
S2 = Rhino.Geometry.Sphere(C2, r2)
Usare il componente C# per Grasshopper:
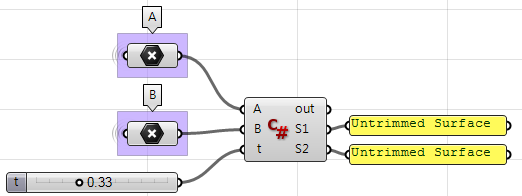
private void RunScript(Point3d A, Point3d B, double t, ref object S1, ref object S2)
{
//declare variables
Rhino.Geometry.Point3d D, C1, C2;
double r1, r2;
//find a point between A and B
D = A + t * (B - A);
//find mid point between A and D
C1 = A + 0.5 * (D - A);
//find mid point between D and B
C2 = D + 0.5 * (B - D);
//find spheres radius
r1 = A.DistanceTo(C1);
r2 = B.DistanceTo(C2);
//create spheres and assign to output
S1 = new Rhino.Geometry.Sphere(C1, r1);
S2 = new Rhino.Geometry.Sphere(C2, r2);
}
Download dei file di esempio
Download del file math-samplesandtutorials.zip contenente tutti gli esempi di Grasshopper e i file del codice menzionati in questa guida.
Passi successivi
Ora che conosciamo la matematica vettoriale, possiamo dare un’occhiata alla guida Matrici e trasformazioni per ulteriori informazioni sugli oggetti da spostare, ruotare e scalare.

