Archimedean Spirals
Windows only

by Dale Fugier (Last updated:  Wednesday, December 5, 2018)

Overview

It is possible to define an Archimedean Spiral with polar coordinates. In polar coordinates $$(r, θ)$$, an Archimedean Spiral can be described by the following equation:

$$r = a+bθ$$

with real numbers $$a$$ and $$b$$. Changing the parameter a will turn the spiral, while $$b$$ controls the distance between successive turnings…

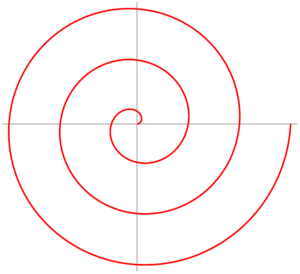
Archimedean Spiral

Sample

Once the polar coordinates have been calculated, we can use RhinoScript’s Polar method to convert them to Cartesian coordinates, which will allow us to plot the curve using RhinoScript’s AddInterpCurve method.

The following sample script code demonstrates how to create an interpolated curve through the points that were calculated using the above equation…

'''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
 ' ArchimedeanSpiral.rvb -- June 2008
 ' If this code works, it was written by Dale Fugier.
 ' If not, I don't know who wrote it.
 ' Works with Rhino 4.0.

 Option Explicit

 Sub ArchimedeanSpiral()

   Dim a_const, b_const, step_angle, num_points
   Dim curr_angle, base_point, radius, points(), i

   Rhino.Print "Archimedean Spiral (r = a + bθ)"

   a_const = Rhino.GetReal("Value of 'A' constant", 1.0, 0.01)
   If IsNull(a_const) Then Exit Sub

   b_const = Rhino.GetReal("Value of 'B' constant", 1.0, 0.01)
   If IsNull(a_const) Then Exit Sub

   num_points = Rhino.GetInteger("Number of points to calculate", 10, 2)
   If IsNull(num_points) Then Exit Sub

   step_angle = Rhino.GetReal("Angle between points", 30.0, 1.0, 45.0)
   If IsNull(step_angle) Then Exit Sub

   curr_angle = 0.0
   base_point = Array(0.0, 0.0, 0.0)
   ReDim points(num_points - 1)

   For i = 0 To UBound(points)
     radius = a_const + (b_const * curr_angle)
     points(i) = Rhino.Polar(base_point, radius, curr_angle)
     curr_angle = curr_angle + step_angle
   Next

   Rhino.AddInterpCurve points
   'Rhino.AddPoints points

 End Sub